5 Variables dummy

Objetivos del capítulo

Al terminar la lectura de este capítulo el lector estará en capacidad de:

• Explicar en sus propias palabras cómo se pueden emplear variables dummy en un modelo de regresión múltiple para probar diferentes hipótesis de trabajo.
• Crear variables dummy utilizando R.
• Estimar modelos econométricos con variables dummy que permitan comprobar diferentes hipótesis.

5.1 Introducción

En los capítulos anteriores hemos discutido el uso de variables que toman valores en un dominio continuo en los modelos de regresión lineal. Sin embargo, en algunas ocasiones será necesario emplear variables que toman únicamente dos valores distintos. Por ejemplo, podría ser necesario incluir en la estimación de un modelo una variable que represente si un individuo es mujer o no, si la observación es de un país que pertenece a determinado grupo económico o no, o si una determinada variable superó un umbral o no, o si la observación corresponde a un trimestre o no.

Empecemos con un ejemplo sencillo para entender el uso de variables Dummy. Supongamos que un gerente de un equipo de fútbol desea saber si el número de entradas vendidas para los partidos de local (\(Y_i\)) difiere si el equipo contrario tiene en su alineación una estrella o no. El científico de datos que tiene a su cargo dar respuesta a esta pregunta de negocio se cuenta con una muestra de \(n\) partidos y solamente dos variables: \(Y_i\) el número de boletas vendidas cuando el equipo es local y una variable \(X_i\) que toma el valor de uno si juega una estrella en el equipo contrario, cero en caso contrario. Una base de datos de estas características se vería algo similar a lo presentado en la Figura 5.1.

Figura 5.1: Ventas de boletas por partido (\(Y_i\)) y presencia de una estrella en el equipo visitante (\(X_i\))

Fuente: elaboración propia.

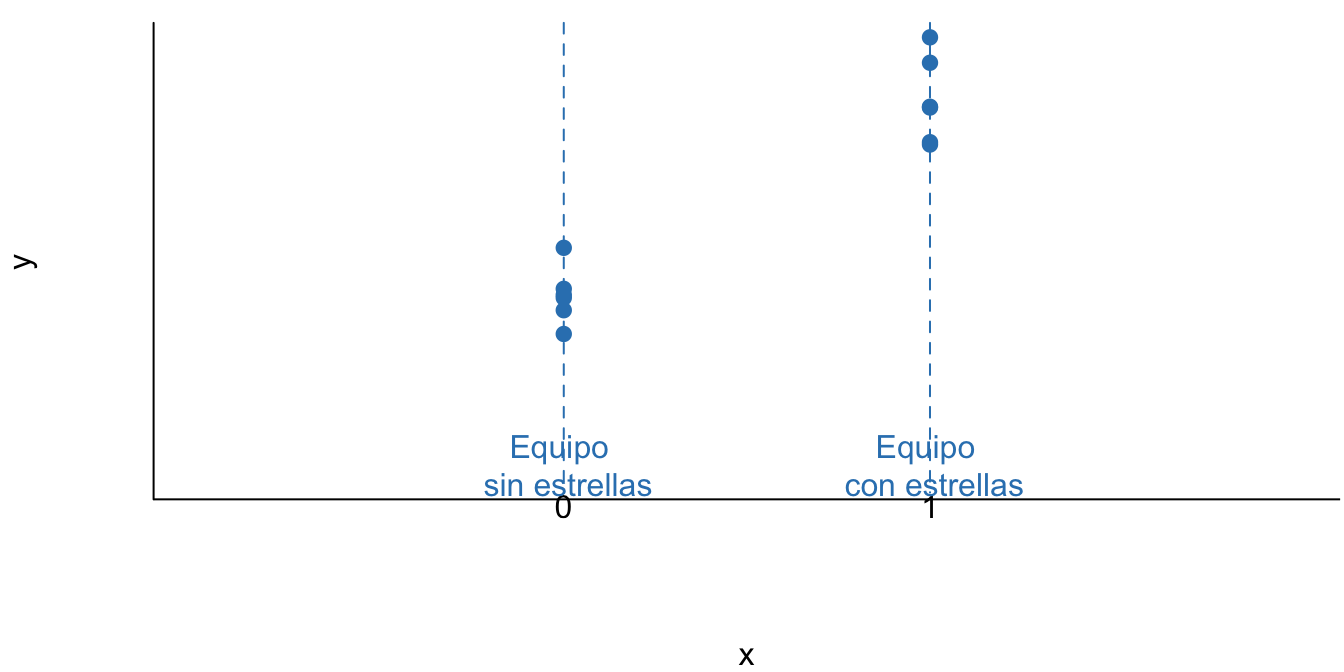
Para este caso, se podría construir el siguiente modelo: \[\begin{equation*} Y_i = \beta_1 + \beta_2 X_i + \varepsilon_i \end{equation*}\] Recordemos que \(X_i = 1\) si juega una estrella en el equipo contrario, cero en caso contrario. En este caso la variable explicativa es una variable cualitativa y no cuantitativa como lo habíamos visto en los capítulos anteriores.

Esta especificación del modelo nos permite modelar las ventas de boletos de diferente manera para las dos situaciones posibles. Es como si tuviésemos dos modelos en uno. Si juega una estrella en el equipo contrario (\(X_i = 1\)) el modelo será: \[\begin{equation*} Y_i = \beta_1 + \beta_2 X_i + \varepsilon_i \end{equation*}\] Y si no juega una estrella (\(X_i = 0\)) el modelo será: \[\begin{equation*} Y_i = \beta_1 + \varepsilon_i \end{equation*}\] Noten que \({\beta_2}\) representa la diferencia en las ventas (promedio) de entradas a los partidos cuando en el equipo contrario juega una súper estrella. De esta manera, la pregunta de negocio se puede resolver estimando el modelo planteado y comprobando inicialmente, si \({\beta_2} = 0\) o no. Si se rechaza la nula de que \({\beta_2} = 0\) se puede proceder a constatar (por medio de pruebas de hipótesis) que la diferencia entre la presentación de una estrella y no tenerla sí es positiva (\(H_0 : \beta_2 \leq 0\)). La Figura 5.2 muestra una representación gráfica de este modelo.

Figura 5.2: Esquema del modelo estimado por MCO

Fuente: elaboración propia.

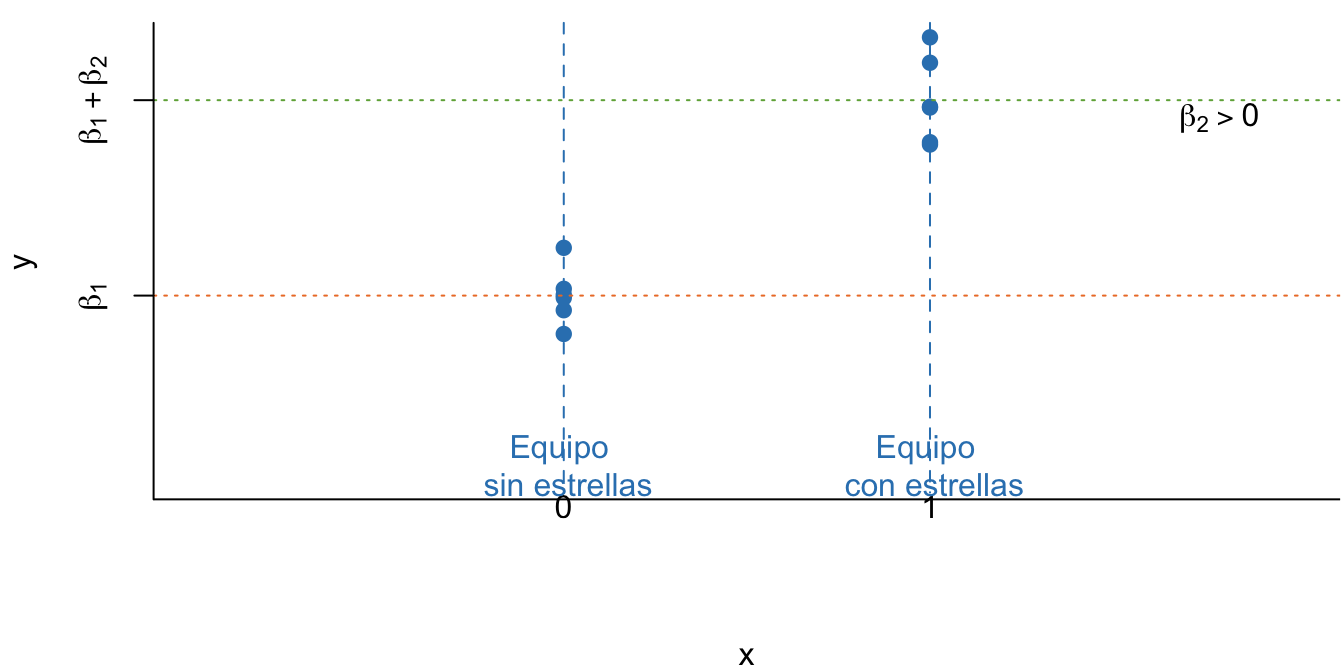
En este capítulo vamos a discutir las variables dummy, también conocidas como variables ficticias, variables indicador o variables dicotómicas. Este tipo de variables pueden ser muy útiles para modelar diferentes fenómenos. Por ejemplo, las variables dummy pueden servir para:

• medir el efecto de “tratamientos” o “intervenciones” sobre la variable de respuesta
• ``borrar’’ el efecto de una observación atípica (ésta es una mejor opción que eliminar las observaciones anormales (outliers))
• incluir un conjunto de categorías
• agrupar las observaciones en diferentes grupos o regiones
• efectos de umbral (Threshold Effects)
• detectar un cambio estructural
• modelar la estacionalidad

Veamos un ejemplo de cómo las variables dummy permiten encontrar el efecto “tratamiento”. En los mercados accionarios se ha encontrado que su comportamiento en promedio no es igual todos los días; es decir, los días se convierten en “tratamientos” diferentes. El efecto del día de la semana (DOW⁴⁹ por su sigla en inglés: Day Of the Week) se puede capturar creando variables dummy para los días de la semana. En este contexto el rendimiento diario de una acción (\(R_t\)) se puede modelar de acuerdo al modelo CAPM⁵⁰ empleando el rendimiento de un activo libre de riesgo (\(R_t^{R.F.}\)) y se puede incluir el efecto DOW de la siguiente manera:

\[\begin{equation*} R_t = \beta_1 + \beta_2 R_t^{R.F.} + \delta_1 D_{1t} + \delta_2 D_{2t} + \delta_3 D_{3t} + \delta_4 D_{4t} + \varepsilon_t \end{equation*}\]

Puedes constatar que este modelo implica un rendimiento promedio para cada día de la semana laboral diferente.

Ahora, concentrémonos en un ejemplo de cómo emplear las variables ficticias para medir el efecto de umbral. Por ejemplo, supongamos que se desea encontrar los determinantes del salario de los empleados de una compañía (\(salario_i\)). Típicamente se emplearía como variables explicativas la edad del empleado como una proxy de la experiencia y los años de educación. Pero podría encontrarse una situación en la cual los años de educación (como una variable continua) no tiene efecto directo sobre el salario, más bien superar unos umbrales de educación si pueden tener un efecto. En este caso el siguiente modelo refleja este efecto de umbral: \[\begin{equation*} salario_i = \beta_1 + \beta_2 age_i + \delta _1 B_i + \delta _2 M_i + \delta _3 P_i + \varepsilon_i \end{equation*}\] donde \(B_i\)= 1 si el máximo título es pregrado y cero en caso contrario. \(M_i\)= 1 si el máximo título es maestría y cero en caso contrario. \(P_i\)= 1 si el máximo título es Ph.D. y cero en caso contrario. Puede demostrar fácilmente cómo este modelo captura un efecto de umbral de los años de educación sobre el ingreso.

Veamos otro ejemplo de efecto de umbral. En algunas ocasiones las ventas de un producto en el período \(t\) (\(V_t\)) pueden reaccionar de manera diferente si el precio (\(p_t\)) sube o baja. Esto se conoce como un comportamiento asimétrico. El modelo de regresión múltiple implica que la reacción de la variable dependiente (en esta caso \(V_i\)) es el mismo cuando una de las variables explicativas aumenta o disminuye. Es decir, el comportamiento es simétrico.

Para capturar este comportamiento asimétrico podemos emplear el siguiente modelo: \[\begin{equation*} V_t = \alpha_1 + \alpha_2 p_t + \delta _1 D_t p_t + \varepsilon_i \end{equation*}\] donde \(D_t =1\) si en el período \(t\) el precio subió y cero en caso contrario. En este caso puedes confirmar que el efecto de un aumento en el precio (\(p_t\)) será diferente a cuando el precio disminuye. Este tipo de efectos también se conocen como un efecto de umbral, siendo el umbral cero. Es decir, \(D_t =1\) si \(p_t - p_{t-1} > 0\). En otras palabras, el efecto de umbral corresponde a cuando es importante tener en cuenta en el modelo el hecho de que una variable supera un determinado valor (umbral).

Continuemos con un ejemplo de cómo emplear las variables dummy para capturar cambio estructural. Por cambio estructural se entiende un cambio en cómo se comporta el DGP a partir de un período determinado. Por ejemplo, el consumo en un país en el período \(t\) (\(C_t\)) puede cambiar su comportamiento después de un período determinado \(t^*\). El cambio (estructural) en la relación del \(C_t\) y del ingreso disponible de los hogares en el período \(t\) (\(Yd_t\)) se puede modelar empleando una variable dummy (\(D_t\)) que toma el valor de uno antes del período \(t^*\) y cero en caso contrario. El modelo sería el siguiente: \[\begin{equation*} C_t = \beta_1 + \beta_2 Yd_t + \alpha D_t + \delta D_t Yd_t + \varepsilon_t \end{equation*}\] Sería conveniente que corroboraras que este modelo implica un cambio tanto en la parte del consumo que no depende del ingreso (intercepto), así como de aquella que si depende de éste (pendiente).

Finalmente, veamos un ejemplo de cómo emplear variables dicotómicas para modelar la estacionalidad de una serie de tiempo (para una discusión amplia sobre este tema ver Alonso & Hoyos (2024)). En la Figura 5.3 se presenta la tasa de desempleo mensual para Colombia. En esta serie se observa una estacionalidad marcada. La estacionalidad es el comportamiento repetitivo que se encuentra en una serie de tiempo en el mismo período al interior de un año (para una discusión amplia sobre este tema ver Alonso & Hoyos (2024)).

Figura 5.3: Tasa de desempleo mensual en Colombia

Fuente: DANE y elaboración propia.

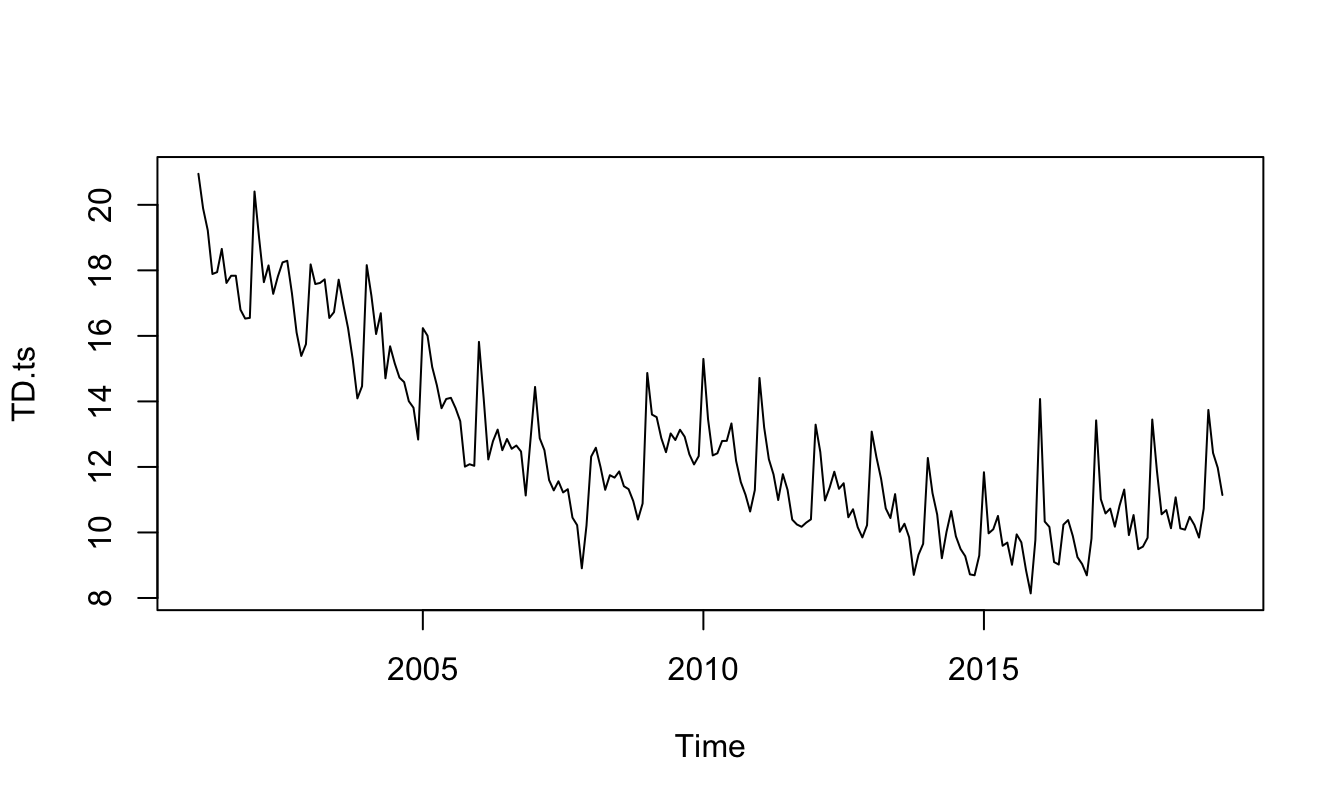
Podemos emplear las variables dicotómicas para desestacionalizar la tasa de desempleo mensual (\(TD_t\)) empleando el siguiente modelo:

\[\begin{equation*} TD_t = \beta_0 + \beta_1 Ene_t + \beta_2 Feb_t + \beta_3 Mar_t + \dots + \beta_{11} Nov_t + \varepsilon_t \end{equation*}\] donde \(Ene_t\) es una variable dummy que toma el valor de uno si el período \(t\) coincide con el mes de enero y cero en caso contrario. De manera análoga, \(Feb_t = 1\) si el mes es febrero y cero en caso contrario. Y de manera similar tendremos variables dummy para los otros meses.

Si se estima dicho modelo, la serie desestacionalizada (\(TD^{desestacionalizada}_t\)) se puede obtener restando el efecto de cada uno de los meses a la serie. Es decir, \[\begin{equation*} TD^{desestacionalizada}_t = TD_t - \left [ \hat{\beta_1} Ene_t + \hat{\beta_2} Feb_t + \hat{\beta_3} Mar_t + \dots + \hat{\beta_3} Nov_t \right ] \end{equation*}\] En la Figura 5.4 se presenta la tasa de desempleo observada y la desestacionalizada que fue obtenida bajo el procedimiento descrito arriba⁵¹.

Figura 5.4: Distribución muestral de la media

Fuente: DANE y elaboración propia.

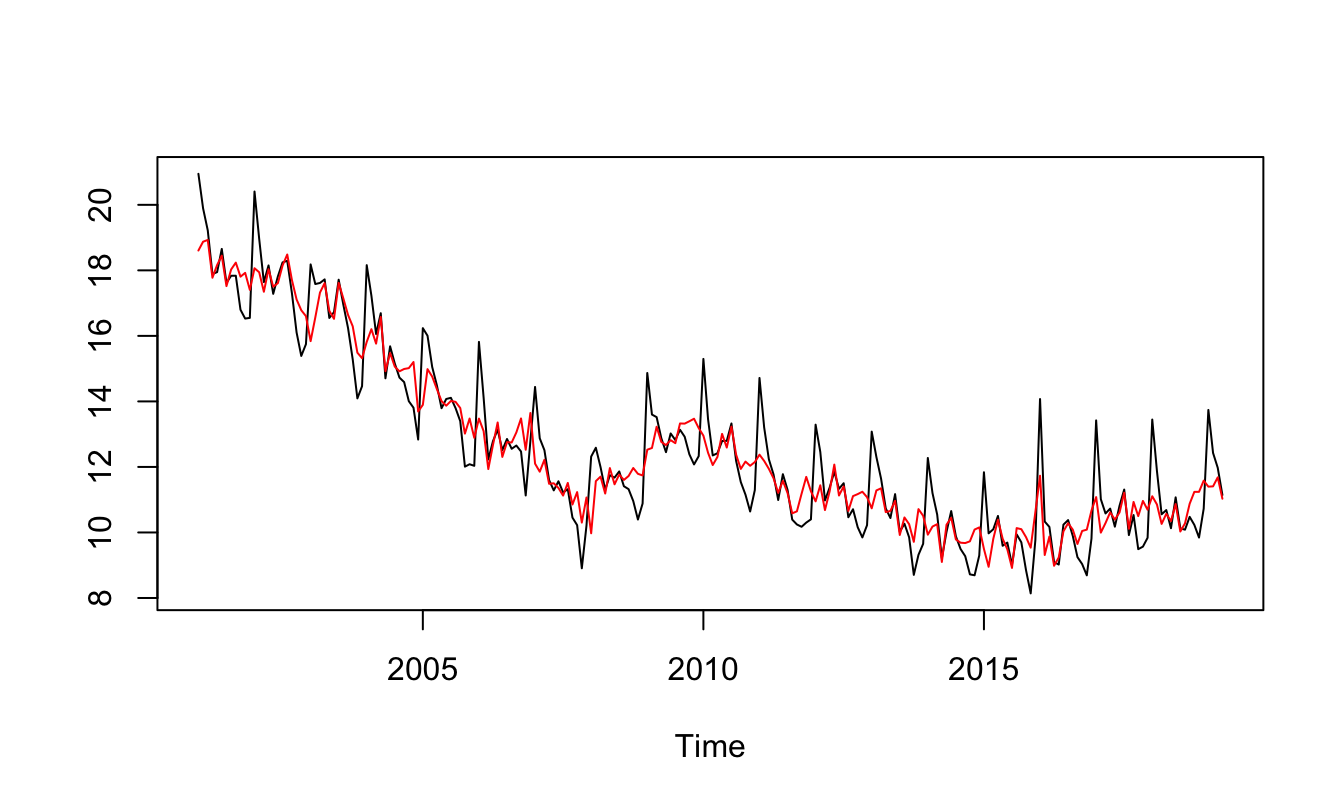
En las siguientes secciones estudiaremos en detalle el efecto de incluir variables dummy. Pero antes de continuar es importante mencionar que cuando se crean variables dummy siempre se deben crear una menos de las opciones disponibles. Esto se hace para evitar lo que se conoce como la “trampa de las variables dummy”.

Es decir, ustedes notarán que en el caso de los días de la semana laboral (efecto DOW) se crearon 4 variables dicotómicas y no 5. Y así para todos los ejemplos descritos anteriormente. En el Capítulo 8 se explicará con mayor claridad el porqué hacemos esto⁵². Por ahora es importante recordar que si existen \(p\) posibilidades, entonces debemos crear \(p-1\) variables ficticias.

5.2 Usos de las variables dummy

Para comprender mejor el uso de las variables ficticias emplearemos un ejemplo sencillo que solo emplea una variable independiente. En esta ocasión emplearemos un modelo para explicar las cantidades vendidas (sell-out) de pasta dental de una marca famosa del país que llamaremos “DBLANCOS” (para mantener el anonimato de la información) por el canal tradicional (tiendas de barrio) en el mes \(t\) (\(Q_t\)). Para lograr este objetivo, el equipo de analítica solo cuenta con una variable continua: la inversión en material promocional que se entrega a las tiendas minoristas en el mes \(t\) (\(I_t\)). Por otro lado, el equipo de analítica al realizar su entendimiento del negocio, ha recibido información del departamento de mercadeo sobre un posible cambio en el comportamiento de las cantidades vendidas en meses donde se venden paquetes de pague 2 lleve 3 frente a períodos en los que no hay ninguna promoción. Afortunadamente se cuenta con información sobre aquellos meses en los que se han realizado promociones de pague 2 lleve 3. En este caso podemos identificar cuatro casos posibles, a continuación veremos cada uno estos casos.

5.3 Caso I. La función es la misma

En este caso se asume que la cantidades vendidas es igual tanto en tiempos de promoción como en tiempos sin promoción. Esto implica la siguiente relación:

\[\begin{equation} Q_t = \beta_1 + \beta_2 I_t + \varepsilon_t \tag{5.1} \end{equation}\]

Como podemos apreciar en la Figura 5.5, tanto la pendiente como el intercepto de la función se mantienen inalterados en todo el período de estudio.

Figura 5.5: Caso I. No hay cambio

Fuente: elaboración propia.

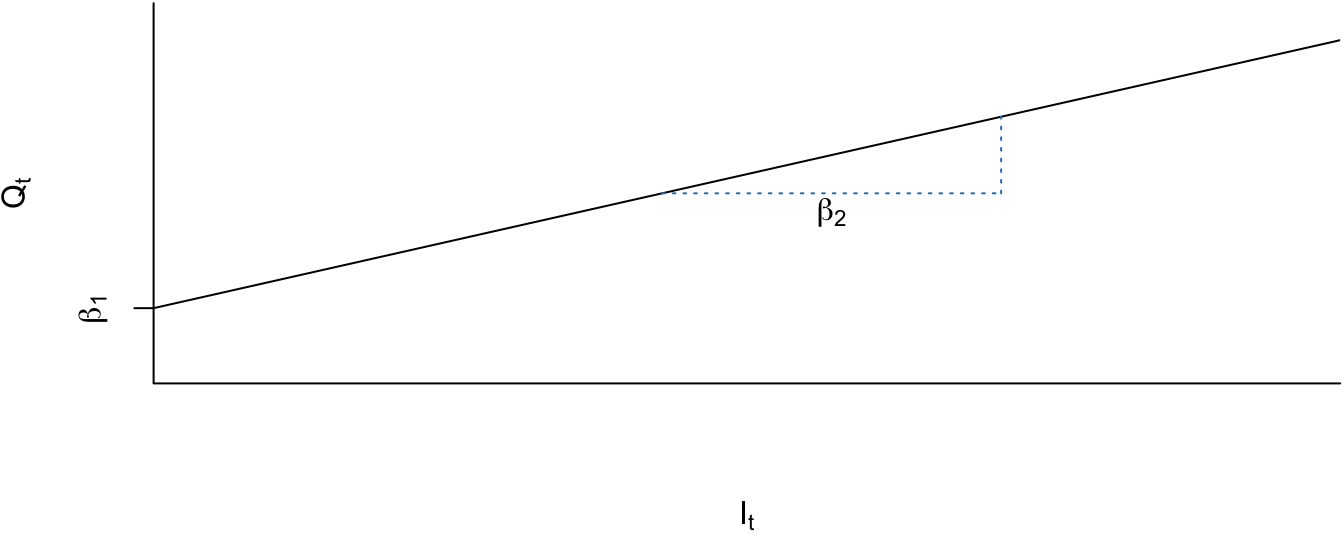
En este caso \(\beta_2\) representa cuántas unidades se venderán por cada peso adicional de ingreso y \(\beta_1\) las cantidades vendidas que no dependen del ingreso. Es decir, un solo modelo para todas las situaciones.

5.4 Caso II. Cambio en intercepto

En el segundo caso, queremos modelar que las unidades vendidas son mayores en períodos con promoción que en tiempos sin promoción (ceteris paribus⁵³). Esto se puede representar con un incremento de las ventas sin importar el nivel de inversión (intercepto de la función) para los meses de promoción, al tiempo que se mantiene inalterada la pendiente. Este efecto lo recoge el siguiente modelo: \[\begin{equation} Q_t = \beta_1 + {\beta_2}{I_t} + \alpha {D_t} + {\varepsilon _t} \tag{5.2} \end{equation}\] donde, \({D_t} = 1\) si se trata de un período con promoción y cero en caso contrario.

Como podemos apreciar, la ecuación (5.2) sugiere que en períodos de promoción (\({D_t} = 1\)) el DGP (modelo) será: \[\begin{equation*} Q_t = \left( \beta_1 + \alpha \right) + \beta_2 I_t + \varepsilon _t \end{equation*}\] En tiempos sin promoción, la variable dummy toma el valor de 0 y, por lo tanto, el modelo que describe cantidades vendidas de cremas de dientes se reduce a: \[\begin{equation*} Q_t = {\beta_1} + {\beta_2}{I_t} + {\varepsilon _t}. \end{equation*}\] La Figura 5.6 representa el modelo ((5.2)).

Figura 5.6: Caso II. Cambio en el intercepto

Fuente: elaboración propia.

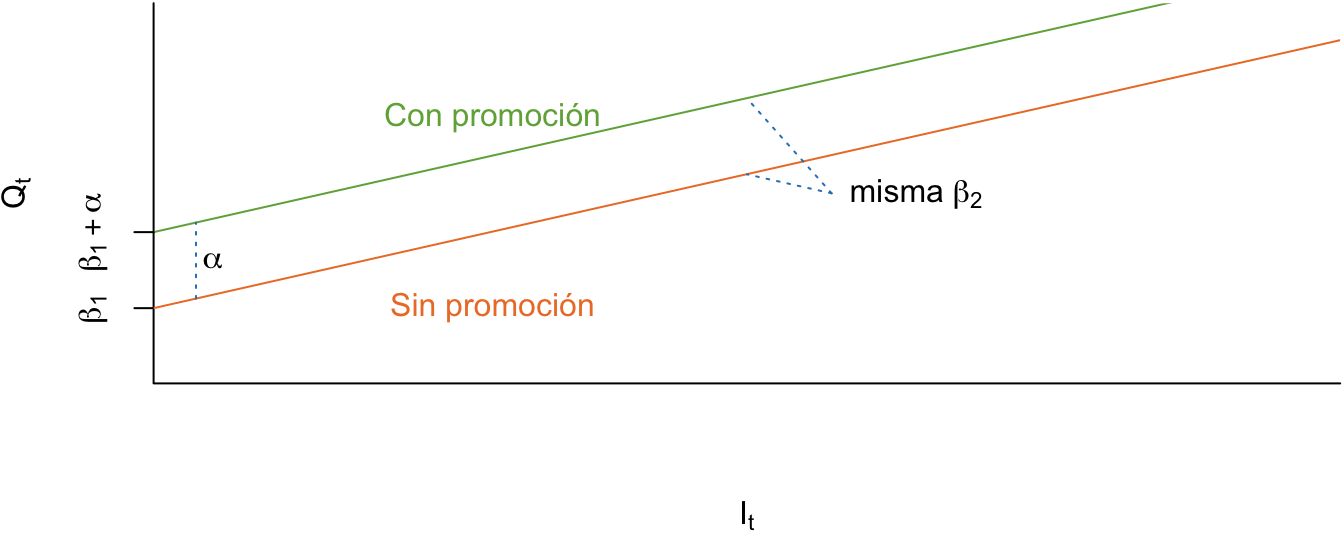
En este caso, \(\alpha\) representa la diferencia del intercepto entre el período sin promoción y con promoción. En otras palabras, la diferencia entre las ventas que no dependen de la inversión entre los meses con promoción y aquellos que no tienen promoción. Además, se espera que \(\alpha > 0\), como se representó en la Figura 5.6. Noten que este caso genera rectas paralelas.

5.5 Caso III. Cambio en pendiente

En este caso, supongamos que las ventas son nuevamente mayor en meses de promoción que en aquellos sin promoción, pero a diferencia del Caso II en el que solo cambiaba el intercepto de la función, en este caso se presenta un cambio de la pendiente (se vende más por cada unidad monetaria adicional de inversión en los meses de promoción). Este hecho lo podemos representar con el siguiente modelo: \[\begin{equation} Q_t = {\beta_1} + {\beta_2}{I_t} + \gamma \left( {{D_t}{I_t}} \right) + {\varepsilon _t} \tag{5.3} \end{equation}\] donde, \({D_t}\) se define igual que antes; igual a uno si se trata de un periodo con promoción y cero en caso contrario.

La ecuación (5.3) nos muestra que en meses con promoción (la variable dummy toma el valor de 1) se presenta un cambio en la pendiente. Es decir, tenemos que en tiempos con promoción el DGP que describe las unidades vendidas toma la siguiente forma: \[\begin{equation*} Q_t = {\beta_1} + \left( {{\beta_2} + \gamma } \right){I_t} + {\varepsilon _t}. \end{equation*}\] En tiempos sin promoción (la variable dummy toma el valor de 0) el DGP viene dado por: \[\begin{equation*} Q_t = {\beta_1} + {\beta_2}{I_t} + {\varepsilon _t}. \end{equation*}\] Este DGP se representa en la Figura 5.7.

Figura 5.7: Caso III. Cambio en pendiente

Fuente: elaboración propia.

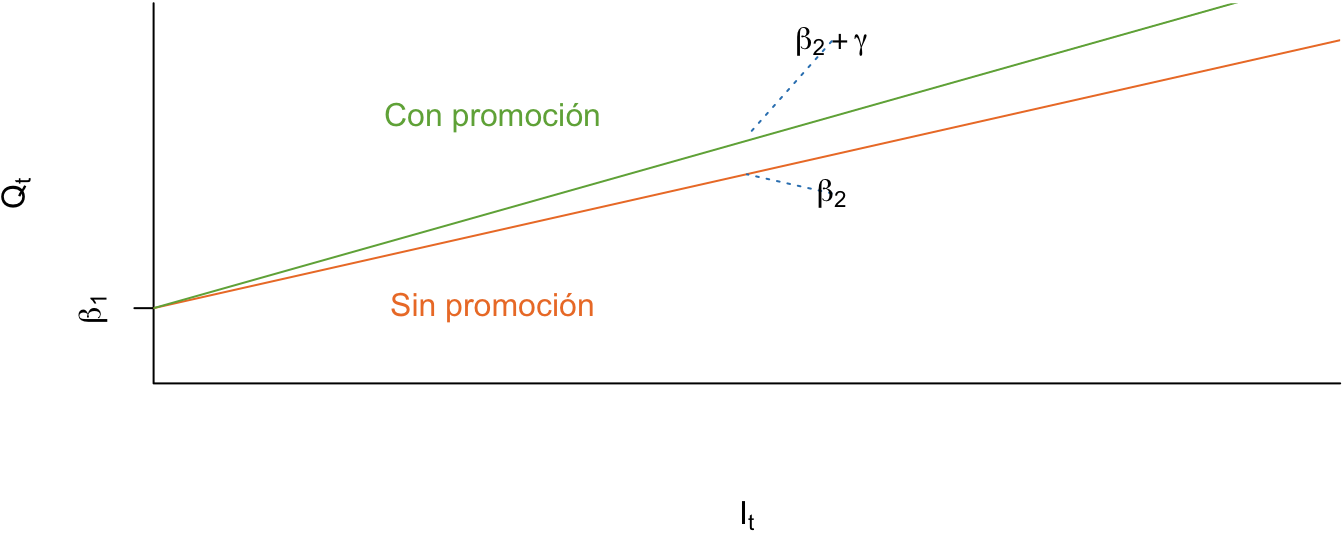
En este caso \(\gamma\) corresponde a la diferencia entre el efecto de una unidad más de inversión sobre las ventas en meses con promoción y sin promoción. En este caso se espera que \(\gamma > 0\), como se representó en la Figura 5.7. Antes de pasar al siguiente caso, es importante mencionar que este tipo de modelos se denominan con interacción entre las variables. Es de decir, la variable dummy interactúa con la variable \(I_t\).

5.6 Caso IV. Cambio en intercepto y pendiente

En este último caso, la venta de cremas dentales aumenta en tiempos con promoción por las dos posibles vías; es decir, por un aumento tanto en el intercepto como en la pendiente. Este efecto es capturado por un modelo con la siguiente especificación: \[\begin{equation} Q_t = \beta_1 + \beta_2 I_t + \alpha D_t + \gamma \left( {D_t I_t } \right) + \varepsilon_t \tag{5.4} \end{equation}\] La variable dummy se define igualmente que en los dos casos anteriores.

Análogamente, el modelo en periodos con promoción será de la siguiente forma: \[\begin{equation*} Q_t = \left( {\beta_1 + \alpha } \right) + \left( {\beta_2 + \gamma } \right)I_t + \varepsilon _t \end{equation*}\]

Figura 5.8: Caso IV. Cambio en intercepto y pendiente

Fuente: elaboración propia.

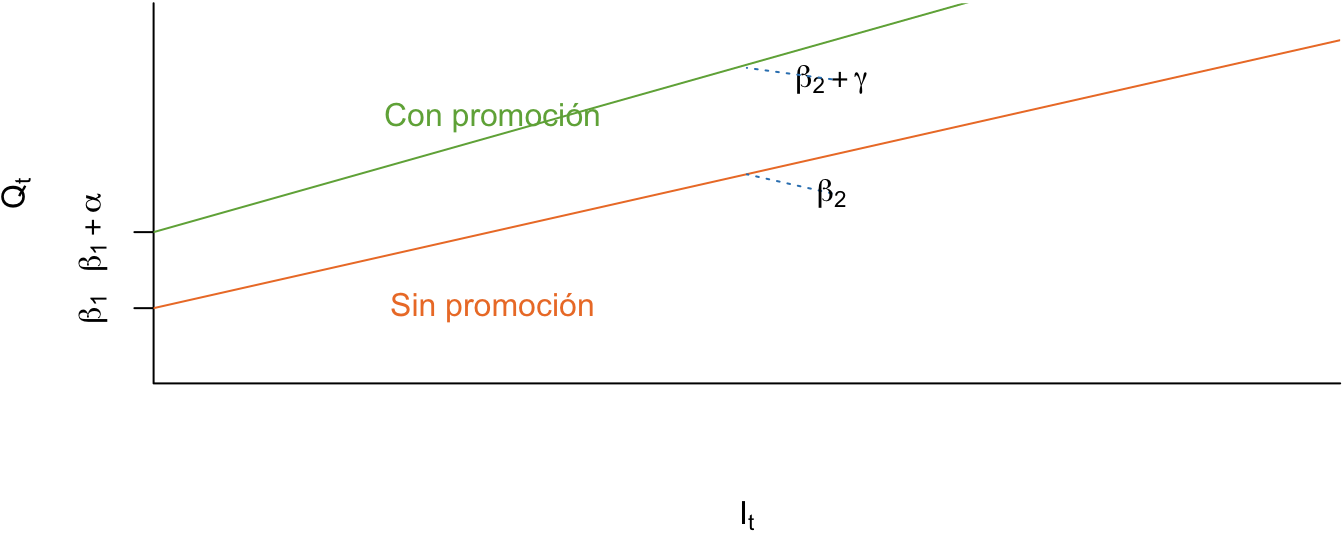
En este caso \(\alpha\) y \(\gamma\) representan la diferencia del intercepto y de la pendiente en periodos con promoción y sin promoción, respectivamente (ver Figura 5.8). Se espera que \(\alpha\) y \(\gamma\) sean positivos.

Para tener en cuenta

En la práctica no podemos saber a cuál de los cuatro casos corresponde el DGP de los datos bajo estudio. Por eso, el científico de datos se ve en la necesidad de probar diferentes especificaciones. En los Capítulos 3 y 4 ya estudiamos métodos estadísticos que nos permitirán escoger entre uno de los casos, para una muestra determinada.

5.7 Práctica en R

Existen múltiples formas de crear variables dummy en R. Por un lado, para mostrar diferentes formas de hacerlos emplearemos dos ejemplos. Por otro lado, es importante mencionar que si una variable es leída como un factor, la función lm() convierte automáticamente dicha variable en una variable dummy⁵⁴. Esto hace que en la mayoría de los casos no sea necesario generar una variable dummy cuando los datos son de corte transversal.

Con este ejercicio ilustraremos cómo generar variables dummy con R en una serie de tiempo. Continuando con el ejemplo de este capítulo, las cantidades vendidas de crema dental de la marca DBLANCOS por el canal tradicional depende de la inversión en material promocional que se entrega a las tiendas minoristas en el mes \(t\). Por otro lado, se considera que la relación ha cambiado a partir del ingreso de las tiendas de descuento en los barrios, como D1 o Justo y Bueno, puesto que le han quitado participación a las tiendas de barrio. Así la pregunta de negocio es ¿qué tanto cambió el impacto de nuestra inversión en material promocional con la entrada de las tiendas de descuento en los barrios?

Como se discutió en la sección anterior, la relación entre estas dos variables implica un modelo lineal como el siguiente: \[\begin{equation} {Q_t} = {\beta_0} + {\beta_1}{I_t} + {\varepsilon_t} \tag{5.5} \end{equation}\] donde \(\beta_0\) representa el intercepto, \(\beta_1\) nos indica cómo cambian las cantidades vendidas de crema dental cuando cambia la inversión en el material promocional en una unidad y \(\varepsilon_t\) un término de error aleatorio.

Los datos para 228 meses se encuentran en el archivo cremadental.csv⁵⁵. Carga los datos y guárdalos en un objeto que llamaremos datos.dummy y cuya clase sea datos.dummy.frame.

Si graficamos las ventas mensuales en el tiempo, observamos un cambio en el comportamiento de estas al final del periodo de análisis (Figura 5.9). Si graficamos la relación entre el sell-in y la inversión en material promocional (Figura 5.10), se observa que ese cambio parece estar afectando tanto el intercepto de la relación como la pendiente. A esto se le denomina cambio estructural. Sin embargo, el análisis gráfico no es suficiente para determinar si en efecto existe un cambio en el intercepto, en la pendiente o en ambos.

Figura 5.9: Evolución de las unidades de Sell-in de la crema dental

Fuente: elaboración propia.

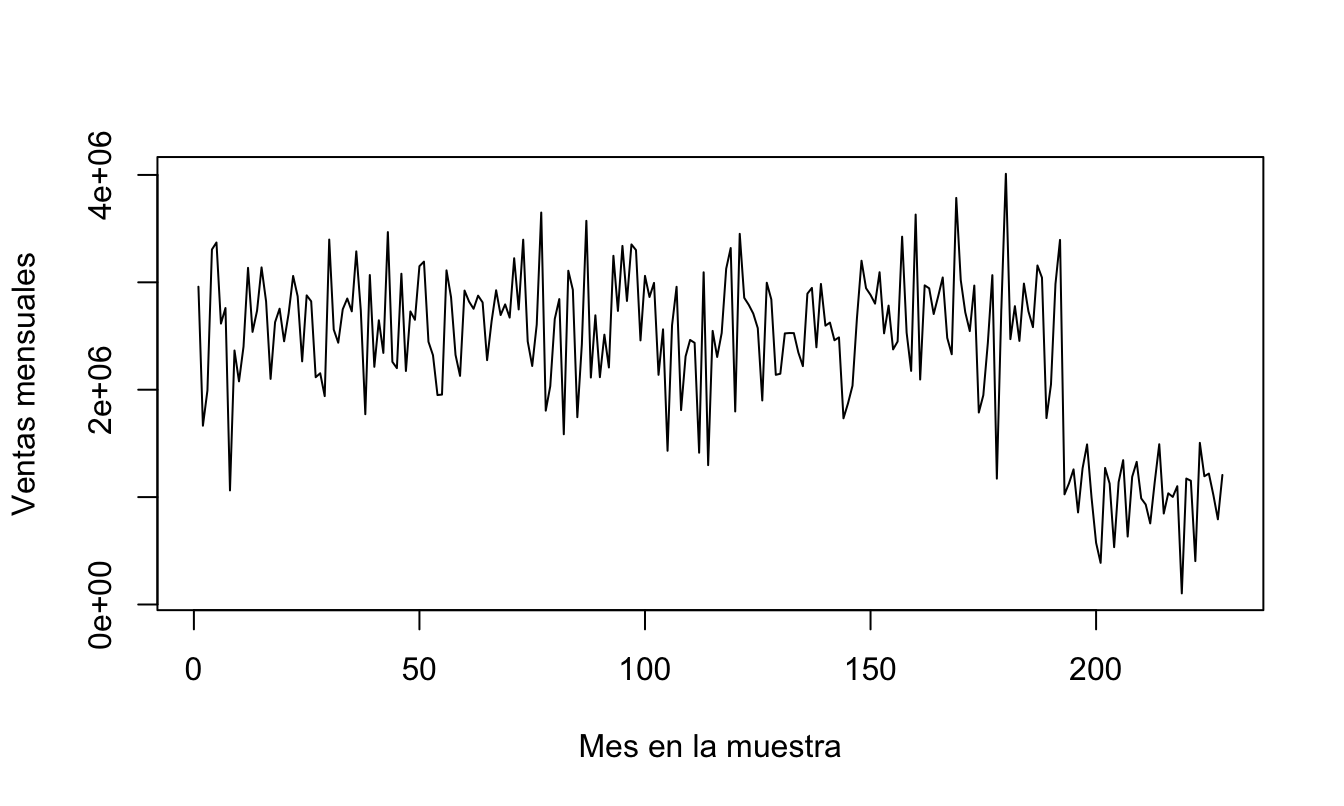
Figura 5.10: Sell-in mensual de crema dental (en unidades) e inversión en material promocional

Fuente: elaboración propia.

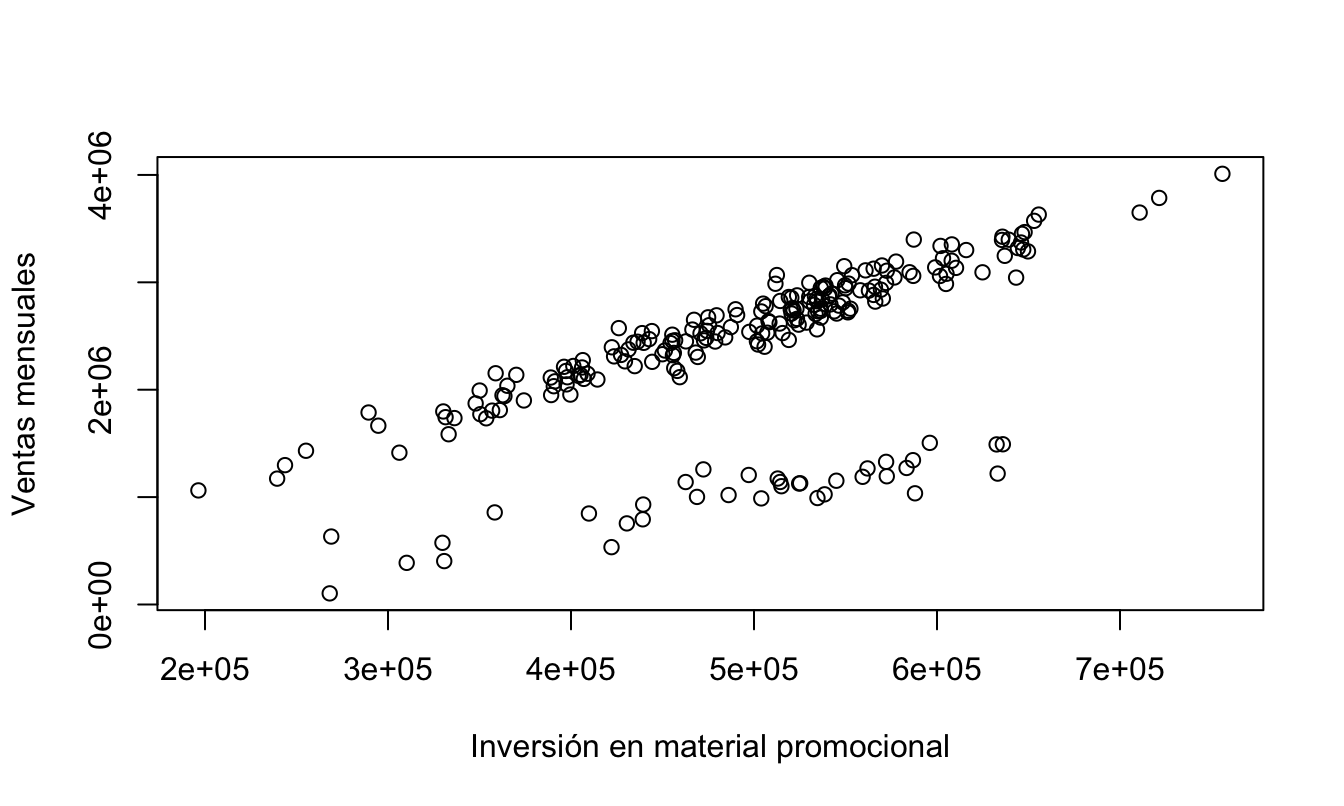
Así parecería que existe una relación diferente para una parte de la muestra, ahora empleando el conocimiento del negocio sabemos que las tiendas de descuento aparecieron a partir de 2009. De esta manera, en este caso (a diferencia de la sección anterior) la variable dummy deberá ser definida como \(D_t\) es 1 si la observación es del año 2009 o posterior y cero en caso contrario.

Para verificar la hipótesis de que la relación ha cambiado después de 2009 se considera el siguiente modelo: \[\begin{equation} {Q_t} = {\beta _0} + {\beta_1}{ingreso_t} + {\alpha _2}{D_t} + {\beta_2}\left( {{D_t}{ingreso_t}} \right) + {\varepsilon _t} \tag{5.6} \end{equation}\] Asegúrate que entiendes por qué este modelo genera un cambio tanto en intercepto como en la pendiente.

Una vez las series sean leídas en R, necesitamos crear esta variable dummy. R provee una variedad de posibilidades para la creación de variables dummy. En este caso emplearemos una prueba lógica sobre la variable año del data.frame datos.dummy.

#Crear dummy con prueba lógica
D <- datos.dummy$año >= 2009
# Convertir clase lógica a numérica e incluir en la base de datos
datos.dummy$D <- as.numeric(D)
# Chequear la creación de la variable
head(datos.dummy,3)

##   inversión       q  año mes D
## 1    566077 2959023 2000   1 0
## 2    294702 1664956 2000   2 0
## 3    350079 1992492 2000   3 0

tail(datos.dummy,3)

##     inversión       q  año mes D
## 226    486103 1019278 2018  10 1
## 227    439214  793211 2018  11 1
## 228    497122 1206111 2018  12 1

datos.dummy[106:115,]

##     inversión       q  año mes D
## 106    475444 2600517 2008  10 0
## 107    537867 2958311 2008  11 0
## 108    361114 1810287 2008  12 0
## 109    423541 2310373 2009   1 1
## 110    519009 2463626 2009   2 1
## 111    439715 2436638 2009   3 1
## 112    306218 1413677 2009   4 1
## 113    624870 3093221 2009   5 1
## 114    243714 1297751 2009   6 1
## 115    474318 2547605 2009   7 1

Ahora sí podemos estimar el modelo deseado (asegúrate que puedes estimarlo). Nota que la interacción entre la variable dummy y la inversión se debe incluir en la fórmula incluyendo D*inversión.

summary(res1)

## 
## Call:
## lm(formula = q ~ D + inversión + D * inversión, data = datos.dummy)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1562566   -96055    74047   399299   764185 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  7.217e+04  2.882e+05   0.250    0.802    
## D           -2.055e+05  3.859e+05  -0.532    0.595    
## inversión    5.125e+00  5.697e-01   8.996   <2e-16 ***
## D:inversión -5.209e-01  7.650e-01  -0.681    0.497    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 550100 on 224 degrees of freedom
## Multiple R-squared:  0.4794, Adjusted R-squared:  0.4724 
## F-statistic: 68.75 on 3 and 224 DF,  p-value: < 2.2e-16

El cambio en el intercepto (coeficiente asociado a \(D_t\)) y el cambio en la pendiente (asociado a \(D_t inversion_t\)) no son individualmente significativos. Es decir, parece que no existe ese cambio estructural después de 2009 cuando llegan las tiendas de descuento a los barrios. No obstante, ya sabemos que no es una buena idea sumar pruebas individuales para tomar una decisión. Entonces es mejor emplear una prueba de modelos anidados que discutimos en el Capítulo 4. En la sección 4.3.1 discutimos cómo corroborar si estos dos coeficientes estimados son iguales a cero simultáneamente. Esto se logra de la siguiente manera:

## Analysis of Variance Table
## 
## Model 1: q ~ inversión
## Model 2: q ~ D + inversión + D * inversión
##   Res.Df        RSS Df  Sum of Sq      F    Pr(>F)    
## 1    226 8.0141e+13                                   
## 2    224 6.7795e+13  2 1.2346e+13 20.396 7.284e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Estos resultados muestran que es posible rechazar la hipótesis nula de que los cambios en pendiente e intercepto son cero simultáneamente. Es decir, podemos concluir que existe un cambio estructural en la relación de las ventas y el ingreso de los tenderos en 2009. Puedes constatar que si se compara el modelo con variables dummy en el intercepto y pendiente con los modelos con solo cambio en intercepto o solo cambio en pendiente se llegará a la conclusión que el mejor modelo es el que tiene el cambio tanto en intercepto como en pendiente⁵⁶. No obstante, individualmente ni el cambio en el intercepto ni el de la pendiente es individualmente significativo.

Ahora continuemos con nuestro análisis de los datos y nuestra tarea de encontrar un buen modelo para explicar las ventas. El modelo que acabamos de obtener no parece el mejor. Ahora, probemos una segunda hipótesis del departamento de mercadeo. En ese departamento se cree que para los años 2016, 2017 y 2018 la relación es diferente dado que las tiendas de descuento ya se habían consolidado y expandido por toda Colombia. Construyamos una dummy segunda (\(D2_t\)) que tome el valor de uno únicamente para los años comprendidos entre 2016 y 2018, periodo donde ya las tiendas de descuento se habían expandido en Colombia.

Olvidémonos por un momento de los resultados encontrados anteriormente y partamos del modelo expresado en (5.1) pero con la variable dummy expresada de la nueva forma. Determine si existe o no un cambio estructural⁵⁷. Los resultados de los tres modelos se presentan en el Cuadro 5.1.

Cuadro 5.1: Estimación del modelo para diferentes especificaciones de la dummy

	res1	res2	res3
(Intercept)	72169.52	-54617.02	74668.03
	(288169.59)	(207448.00)	(49871.48)
D	-205487.43
	(385894.24)
inversión	5.12***	4.89***	5.13***
	(0.57)	(0.41)	(0.10)
D:inversión	-0.52
	(0.76)
D2			-472231.02***
			(119814.75)
D2:inversión			-2.24***
			(0.24)
R2	0.48	0.38	0.97
Adj. R2	0.47	0.38	0.97
Num. obs.	228	228	228
***p < 0.001; **p < 0.01; *p < 0.05

Noten que en esta última ecuación estimada, el cambio en la pendiente e intercepto sí son significativos individualmente (con un nivel de confianza del 99%). Y conjuntamente también lo son a un nivel de significancia del 99%, como se muestra a continuación:

## Analysis of Variance Table
## 
## Model 1: q ~ inversión
## Model 2: q ~ D2 + inversión + D2 * inversión
##   Res.Df        RSS Df  Sum of Sq      F    Pr(>F)    
## 1    226 8.0141e+13                                   
## 2    224 3.7944e+12  2 7.6347e+13 2253.5 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Así, podemos rechazar la hipótesis nula que no existió cambio en la pendiente y el intercepto para los últimos 3 años. La evidencia muestra que este último modelo explica mucho mejor la muestra que tenemos al frente y, por tanto, debería ser el indicado para tomar decisiones.

5.7.1 Creando variables dummy con paquetes de R

En algunas ocasiones será necesario crear las variables dummy en vez de dejar que la función lm() las cree automáticamente. Por ejemplo, suponga que tenemos datos para todos los días de la semana en la base de datos y solo queremos crear variables dummy para los cinco días laborales. Si empleamos esta variable con la función lm(), ésta creará seis variables dummy para todos los días de la semana (y descarta una). En ese caso podemos emplear paquetes de R para hacer esta tarea más rápidamente. La verdad no existe un mejor paquete para crear variables dummy, solo unos funcionan mejor que otros en diferentes circunstancias.

Una opción es el paquete fastDummies (Kaplan, 2020). Este paquete tiene la función dummy_cols() que permite al mismo tiempo que se crea la variable dummy descartar una de ellas. Esta función implica por lo menos los siguientes argumentos:

dummy_columns(data, select_columns = NULL, remove_first_dummy = FALSE, remove_most_frequent_dummy = FALSE, ignore_na = FALSE, split = NULL, remove_selected_columns = FALSE, omit_colname_prefix = FALSE)

donde:

• data: es un objeto de clase matriz o data.frame.
• select_columns: si se emplea un data.frame este es un vector con los nombres de las variables a las que se les desea crear las variables dicotómicas.
• remove_most_frequent_dummy: Si remove_most_frequent_dummy = TRUE se elimina la dummy para la categoría en la que exista más observaciones. Si este argumento es igual a FALSE, entonces no se remueve ninguna variable dummy. Esta última opción es la que se ejecuta por defecto.
  
• ignore_na: Cuando ignore_na = FALSE (opción por defecto) se crea una variable dummy cuando se encuentra un “NA” en la variable a ser transformada. Si ignore_na = TRUE entonces se omite las observaciones con “NA”, no se crea una nueva variable y a esa observación se le asigna “NA” en todas las dummies que se creen (Esta es la opción recomendada en la mayoría de los casos).

Empleemos esta función con un data.frame similar al anterior, pero adicionemos datos perdidos en la variable que transformaremos.

ventas <- data.frame(ciudades = c("Cali", "Medellin", "Bogotá", "Cali", NA),
                    año = c(2019, 2020, 2020, 2020, 2019),
                    ventas = c(10, 30, 40, 15, NA))
ventas$ciudades <- as.factor(ventas$ciudades)
str(ventas)

## 'data.frame':    5 obs. of  3 variables:
##  $ ciudades: Factor w/ 3 levels "Bogotá","Cali",..: 2 3 1 2 NA
##  $ año     : num  2019 2020 2020 2020 2019
##  $ ventas  : num  10 30 40 15 NA

Ahora, veamos diferentes opciones al aplicar esta función.

library(fastDummies) 
dummy_cols(ventas$ciudades)

##      .data .data_Bogotá .data_Cali .data_Medellin .data_NA
## 1     Cali            0          1              0        0
## 2 Medellin            0          0              1        0
## 3   Bogotá            1          0              0        0
## 4     Cali            0          1              0        0
## 5     <NA>           NA         NA             NA        1

Quitemos la variable dummy para la opción que más se repite y descartemos la opción de crear una dummy para las observaciones no disponibles (“NA”).

dummy_cols(ventas$ciudades, remove_most_frequent_dummy = TRUE,
             ignore_na = FALSE)

##      .data .data_Bogotá .data_Medellin
## 1     Cali            0              0
## 2 Medellin            0              1
## 3   Bogotá            1              0
## 4     Cali            0              0
## 5     <NA>           NA             NA

Hagamos lo mismo, pero empleando el data.frame y no la columna:

dummy_cols(ventas, select_columns = "ciudades", 
           remove_most_frequent_dummy = TRUE,
             ignore_na = FALSE)

##   ciudades  año ventas ciudades_Bogotá ciudades_Medellin
## 1     Cali 2019     10               0                 0
## 2 Medellin 2020     30               0                 1
## 3   Bogotá 2020     40               1                 0
## 4     Cali 2020     15               0                 0
## 5     <NA> 2019     NA              NA                NA

5.8 Ejercicios

Las respuestas a estos ejercicios se encuentran en la sección 16.3.

5.8.1 Continuación Ejercicio DBLANCOS

Continuemos con el ejemplo realizado en este capítulo y estudiemos en más detalle los posibles modelos que se podían estimar con la dummy definida como: \(D_t = 1\) si \(t\) es del año 2009 o posterior y cero en caso contrario.

Estima un modelo sin variables dummy, con solamente cambio en la pendiente, otro con solo cambio en el intercepto y con cambio en ambos. Ahora, decide cuál modelo es mejor: sin cambios, con dummy solo en intercepto, solo en pendiente, o con dummy en ambos.

Referencias

Alonso, J. C., & Berggrun, L. (2011). Intrducción al análisis de riesgos financiero. Ecoe Ediciones.

Alonso, J. C., & Gallo, B. E. (2013). The Day-of-the-Week Effect: The CIVETS Stock Markets Case. Journal of Applied Business and Economics, 15(3), 102–116.

Alonso, J. C., & Hoyos, C. C. (2024). Introducción a los pronósticos con modelos estadístico de series de tiempo para científico de datos (en R) (Universidad Icesi). Universidad Icesi.

Kaplan, J. (2020). fastDummies: Fast creation of dummy (binary) columns and rows from categorical variables. https://CRAN.R-project.org/package=fastDummies

---

49. Ver Alonso & Berggrun (2011) para una introducción al modelo CAPM y Alonso & Gallo (2013) para una discusión del DOW.↩︎

50. Ver Alonso & Berggrun (2011) para una introducción al modelo CAPM.↩︎

51. Existen otras formas de desestacionalizar una serie, pero estas están por fuera del alcance de este libro. Para una discusión de las técnicas de desestacionalizar, se puede consultar Alonso & Hoyos (2024).↩︎

52. Si se incluyen variables dummy para todas las opciones, una de estas variables no trae información nueva al modelo; en otras palabras esa variable será redundante. Esto implicará que las variables no son independientes y por tanto se violará un supuesto del teorema de Gauss-Markov. Por ejemplo, supongamos que en un modelo se desea incluir el sexo del individuo como una variable explicativa. Para esto se crea una variable dummy \(M_i\) que toma el valor de uno si el individuo \(i\) es mujer y cero en caso contrario. Adicionalmente, se crea la variable \(H_i\) que toma el valor de uno si \(i\) es hombre y cero en caso contrario. Ahora noten que si para un determinado individuo \(i\) \(M_i=1\), entonces tiene que ser cierto que \(H_i=0\). Adicionalmente, si \(M_i=0\), entonces \(H_i=1\). Esto implica que \(H_i\) es una variable que sobra dado que su valor lo podemos conocer con seguridad del valor que tome \(M_i\).↩︎

53. El término ceteris paribus significa dejando todo lo demás constante.↩︎

54. Si se desea cambiar el grupo de referencia (el valor para el cual la dummy toma el valor de cero), se puede emplear la función relevel() que toma como argumentos la variable del data.frame que se quiera cambiar y ref que permite escribir el nombre del nivel del factor (entre comillas) que se quiere emplear como la referencia. Por ejemplo, de la siguiente manera relevel(data.frame$variable, ref = “SI”).↩︎

55. Los datos se pueden descargar de la página web del libro: https://www.icesi.edu.co/editorial/modelo-clasico/↩︎

56. Este corresponde al primer ejercicio de este capítulo.↩︎

57. Ayuda: puedes emplear el signo & para hacer dos pruebas lógicas al mismo tiempo.↩︎