9 Heteroscedasticidad

Objetivos del capítulo

Al finalizar este capítulo, el lector estará en capacidad de:

• Explicar en sus propias palabras los efectos de la heteroscedasticidad sobre los estimadores MCO.
• Efectuar utilizando R las pruebas estadísticas necesarias para detectar la violación del supuesto de homoscedasticidad en los residuos. En especial las pruebas de Breusch-Pagan y la prueba de White.
• Corregir el problema de heteroscedasticidad empleando estimadores consistentes para los errores estándar en R.

9.1 Introducción

Como lo hemos discutido en capítulos anteriores, si los supuestos del modelo de regresión se cumplen, entonces el Teorema de Gauss-Markov demuestra que los estimadores MCO son MELI (Mejor Estimador Lineal Insesgado). En el Capítulo 8 analizamos las consecuencias de la violación del supuesto de independencia lineal entre variables explicativas en un modelo de regresión múltiple; es decir la presencia de multicolinealidad. También discutimos cómo dicho problema era un problema de los datos y que en ocasiones no será necesario resolver el problema. En este capítulo nos concentramos en la violación del supuesto que el término de error tiene varianza constante.

Supuestos del modelo de regresión múltiple

En resumen, los supuestos del modelo de regresión múltiple son:

1 Relación lineal entre \(y\) y \({X_2},{X_3},...,{X_k}\)

2 \({X_2},{X_3}, \cdots, {X_k}\) son fijas y linealmente independientes (la matriz \(X\) tiene rango completo)

3 El vector de errores \({\bf {\varepsilon}}\) satisface:

• Media cero \(E\left[ {\bf {\varepsilon}} \right] = 0\)
• Varianza constante
• No autocorrelación.

Es decir, \(\varepsilon_i \sim i.i.d\left( {0,\sigma^2} \right)\) o \(\varepsilon _{n \times 1} \sim \left( \bf {0_{n \times 1}},\sigma^2{\bf {I_n}} \right)\).

Antes de concentrarnos en la violación del supuesto, veamos un poco la intuición detrás del cumplimiento de este supuesto. En la Figura 9.1 se presenta una muestra de observaciones para una variable explicativa (\(X_1\)) y una dependiente (\(y\)) (puntos grises) en la que se cumple el supuesto de homoscedasticidad. El supuesto de homoscedasticidad implica que la dispersión de las observaciones (puntos) con respecto al modelo de regresión poblacional (línea de regresión) será siempre la misma (Ver Figura 9.1). El tercer eje mide la probabilidad de que ocurra un valor de \(y\) dado el valor de \(X_1\). En este caso esperamos que en promedio los valores de \(y\) se encuentren cercanos a la línea de regresión (por el supuesto de que \(E\left[ \varepsilon \right] = 0\) y el supuesto de homoscedasticidad implica que la dispersión con respecto a la linea de regresión siempre es la misma.

Figura 9.1: Muestras con errores homoscedasticidad

Fuente: elaboración propia.

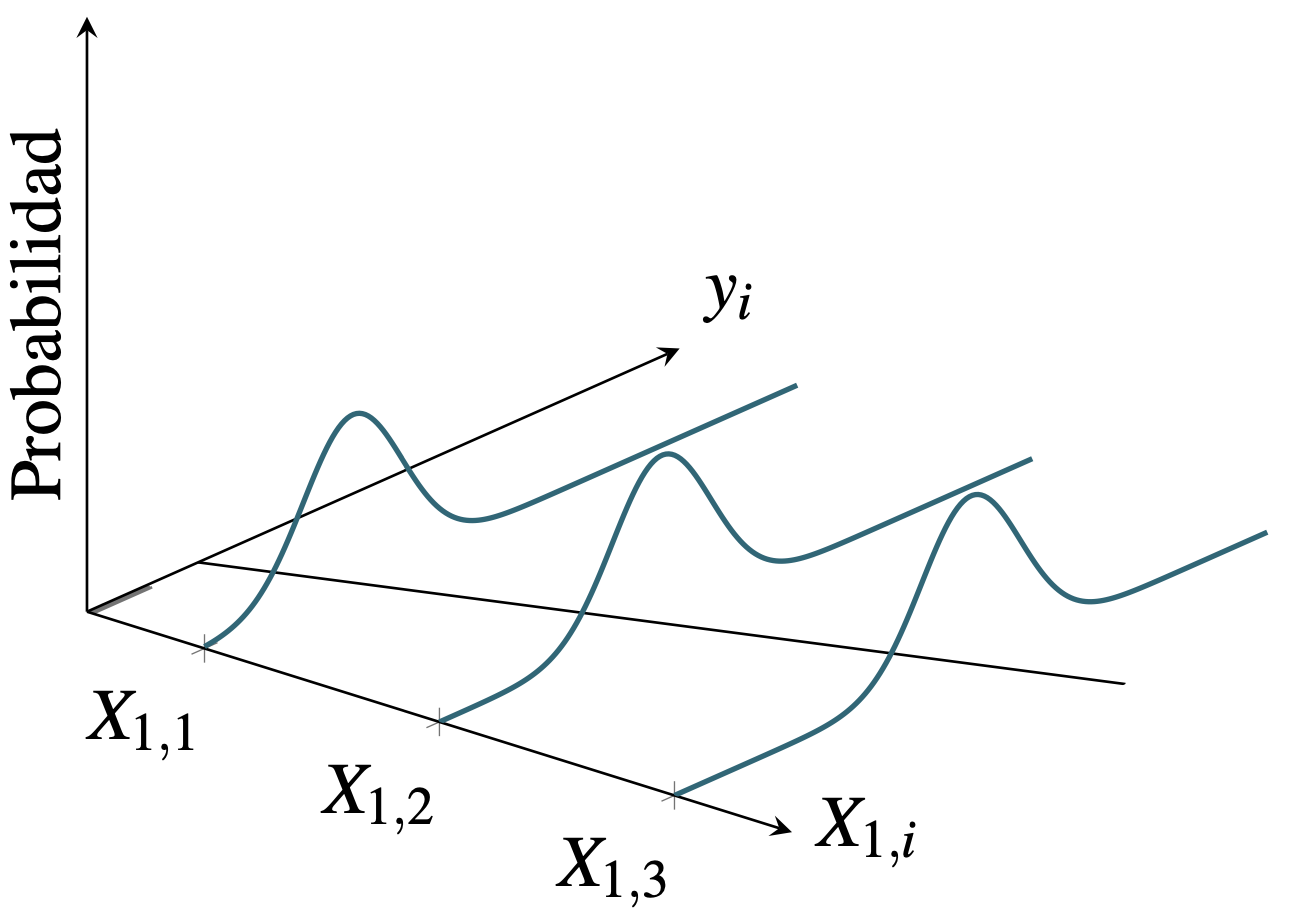
Por otro lado, si el supuesto no se cumple entonces las observaciones de \(y\) seguirán estando en promedio alrededor de la linea de regresión (Ver Figura 9.2) gracias al supuesto de que \(E\left[ \varepsilon \right] = 0\)). La heteroscedasticidad provoca que la dispersión sea diferente dependiendo de la observación. En este caso en la Figura 9.2 se simuló un problema de heteroscedasticidad que depende del valor de la variable explicativa. La volatilidad es mayor a medida que \(X_1\) se hace más grande⁹³.

Figura 9.2: Muestras con errores heteroscedasticidad

Fuente: elaboración propia.

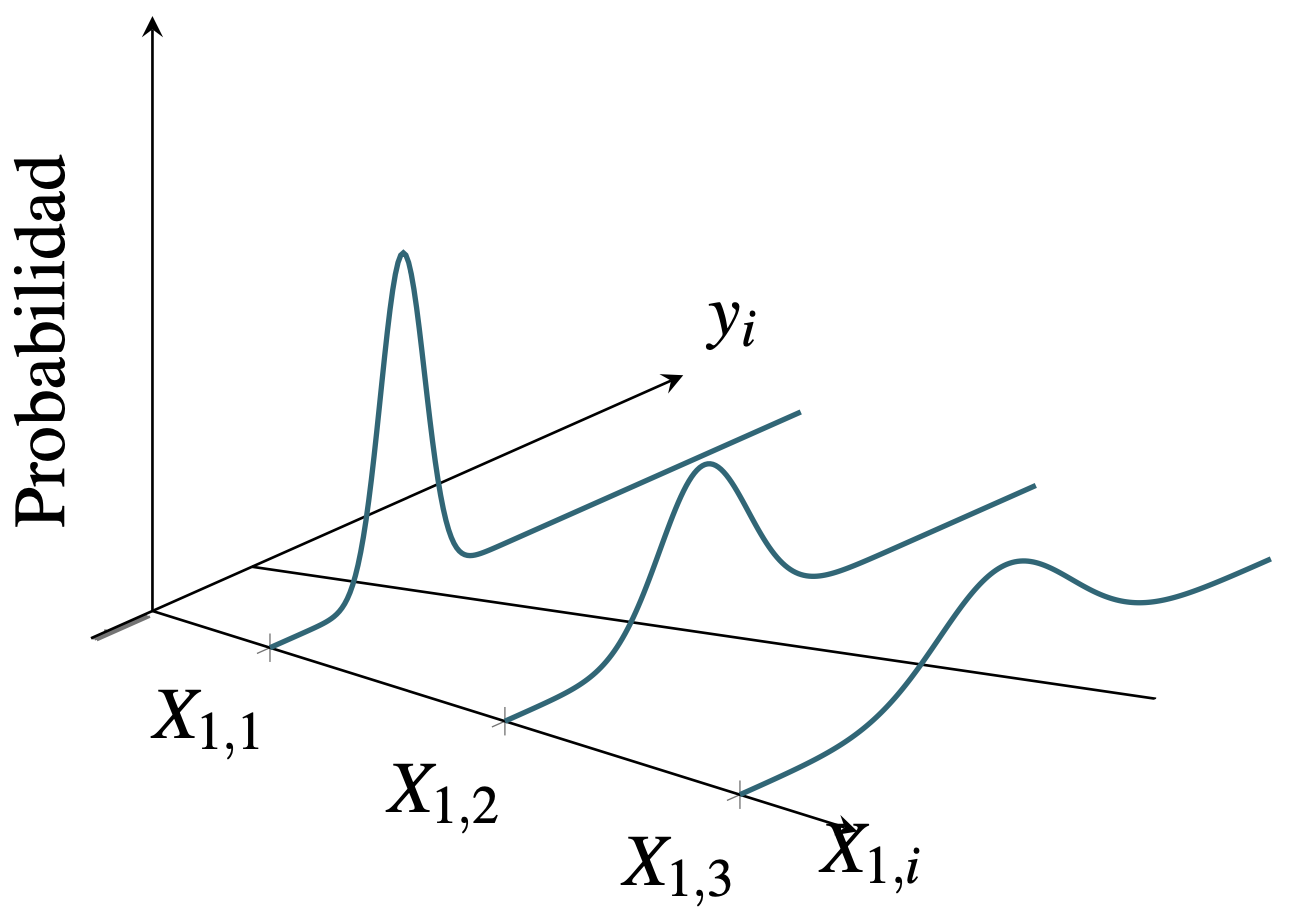
En ocasiones el supuesto de homoscedasticidad o varianza constante del término de error no tiene mucho sentido. Un ejemplo de esto se presenta al analizar el consumo en función del ingreso con una muestra de hogares (corte transversal). Supongamos que se desea emplear un modelo en que las compras de un producto del hogar \(i\) para lo cual se cuenta con una base de datos amplia para muchos niveles de ingresos. Las compras entre muchas cosas dependen de su nivel de ingresos y otras variables que caracterizan la condición socio demográfica del hogar. Los hogares con ingresos bajos típicamente presentan un comportamiento de compra mucho menos variable que el consumo de los hogares con altos ingresos. Es decir, es de esperarse que para ingresos altos el comportamiento del consumo se disperse más con respecto a lo esperado (su media). Por otro lado, a medida que el ingreso sea más bajo los hogares no podrán tener una dispersión muy grande con respecto a lo esperado para su nivel de ingresos. Esto implica que las observaciones correspondientes al consumo de hogares con ingresos bajos tendrán una varianza con respecto a su valor esperado (varianza del error) mucho menor que aquellos hogares con ingresos altos. También existen otras razones para que se presente la heteroscedasticidad, como por ejemplo el aprendizaje sobre los errores y mejoras en la recolección de la información a medida que ésta se realiza.

En general, este problema econométrico es muy común en datos de corte transversal, aunque es posible que el problema también se presente con series de tiempo; especialmente si se están modelando rendimientos de activos o el valor de activos financieros como las acciones. Formalmente, en presencia de este problema, la matriz de varianzas y covarianzas de los errores será: \[\begin{equation*} Var\left[ \varepsilon \right] = E\left[ {{\varepsilon ^T}\varepsilon } \right] = \Omega = \left[ {\begin{array}{*{20}{c}} {\sigma _1^2} & 0 & \ldots & 0 \\ 0 & {\sigma _2^2} & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & 0 & \ldots & {\sigma _n^2} \\ \end{array}} \right] \ne {\sigma ^2}I. \end{equation*}\]

En presencia de heteroscedasticidad, los estimadores MCO siguen siendo insesgados, pero ya no tienen la mínima varianza posible⁹⁴. Es decir, los estimadores MCO no son MELI.

De hecho, el estimador MCO de la matriz de varianzas y covarianzas (\(Var\left[ {\hat \beta } \right] = {\sigma ^2}{\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}\)) será sesgado. En presencia de heteroscedasticidad la matriz de varianzas y covarianzas del estimador MCO del vector \(\beta\) es⁹⁵: \[\begin{equation*} Var\left[ {\hat \beta } \right] = {\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}{{\bf{X}}^{\bf{T}}}\Omega {\bf{X}}{\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}} \end{equation*}\] Esto implica que el estimador de la matriz de varianzas y covarianzas \(\widehat{Var\left[ {\hat \beta } \right]} = {s^2}{\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}\) sea sesgado; y por lo tanto, si usamos este último estimador en pruebas de hipótesis o intervalos de confianza para los coeficientes estimados obtendremos conclusiones erróneas en torno a los verdaderos \(\beta\)s. Esto ocurrirá en las pruebas individuales y conjuntas.

Así, si se emplea el estimador MCO en presencia de heteroscedasticidad, entonces los estimadores de los coeficientes serán insesgados, pero los errores estándar no serán los adecuados. Por tanto, cualquier conclusión derivada de la inferencia a partir de los estimadores MCO será incorrecta.

Antes de continuar hagamos un ejercicio similar al realizado en el Capítulo 3 para ejemplificar el problema que genera la heteroscedasticidad. Realicemos el siguiente experimento de Monte Carlo. Creemos una muestra de datos de tamaño 50 del siguiente DGP: \[\begin{equation*} Y_i = 1 + 7 X2_{i} + \varepsilon_i \end{equation*}\]

donde \(\varepsilon_i\) puede ser homoscedástico y heteroscedástico. Nuestro experimento tendrá como finalidad ver cuál es el efecto sobre los estimadores MCO y su desviación estándar (errores estándar) de la heteroscedasticidad. Adicionalmente, crearemos una segunda variable explicativa \(X3_i\) que no es significativa y la incluiremos en nuestro análisis.

En otras palabras, generaremos una muestra aleatoria del DGP con errores homoscedásticos y otra con errores heteroscedásticos y estimaremos los correspondientes coeficientes. Y repetiremos este ejercicio 10 mil veces. Al final tendremos una muestra de 10000 para cada coeficiente estimado para cada uno de los escenarios: con y sin heteroscedásticidad. Esto nos permitirá determinar si el promedio de los coeficientes coincide o no con el valor poblacional (es insesgado) y comparar las varianzas del estimador MCO en presencia o no de este problema.

Empecemos nuestro experimento fijando una semilla para los número aleatorios y creando los objetos donde guardaremos los resultados de las simulaciones. Así mismo definamos los parámetros del tamaño de la muestra y el número de repeticiones.

# se fija una semilla
set.seed(1234557)
# se crean objetos para guardar resultados
 # creamos un objeto nulo para guardar los coeficientes de X2
 X2.estcoef <- NULL
 # creamos un objeto nulo para guardar los coeficientes de X3
 X3.estcoef <- NULL 
# se fija el tamaño de cada muestra en 50
 n=50
 
# se fija el número de repeticiones en 10mil 
 N=10000

Ahora empleemos un loop para replicar nuestro ejercicio 100 mil veces.

for (i in 1:N){
        # creación de variable explicativa
        X2 <- matrix(rnorm(n),n,1)  
        # creación de variable no significativa
        X3 <- matrix(rnorm(n),n,1) 
        # error homoscedástico
        err <- rnorm(n) 
        # error heteroscedástico
        herr <- (X2^2)*err 
        # variable explicativa sin heteroscedasticidad
        y1 <- 1 + X2*7 + err 
        # variable explicativa con heteroscedasticidad
        y2 <- 1 + X2*7 + herr 
        # estimación del modelo con homoscedasticidad
        res.homo <- summary(lm(y1 ~ X2 + X3)) 
        
        # guardamos los resultados regresión homoscedasticidad
        X2.cf.homo<-res.homo$coefficients[2,1] 
        X3.cf.homo<-res.homo$coefficients[3,1]

        # estimación del modelo con heteroscedasticidad
        res.hetero <- summary(lm(y2 ~ X2 + X3)) 
        # guardamos los resultados regresión heteroscedasticidad
        X2.cf.hetero <- res.hetero$coefficients[2,1]
        X3.cf.hetero <- res.hetero$coefficients[3,1]
        # guardando los resultados de la iteración i
        X2.estcoef<-rbind(X2.estcoef,cbind(X2.cf.homo, X2.cf.hetero))
        X3.estcoef<-rbind(X3.estcoef,cbind(X3.cf.homo, X3.cf.hetero))

        }

Ahora, comparemos los resultados para el caso de un error homoscedástico y uno heteroscedástico para la pendiente que acompaña a \(X2_{i}\). Primero veamos el promedio de los 10 mil coeficientes estimados en los dos escenarios.

round(apply(X2.estcoef,2,mean),3)

##   X2.cf.homo X2.cf.hetero 
##        6.999        6.997

Se puede observar que en ambos escenarios en promedio los coeficientes estimados están muy cercanos al valor poblacional de 7. Ahora miremos que ocurre con el error estándar (desviación estándar de los coeficientes estimados).

round(apply(X2.estcoef,2,sd), 2)

##   X2.cf.homo X2.cf.hetero 
##         0.15         0.52

Noten que el error estándar es menor en el escenario de homoscedasticidad que en el de heteroscedasticidad. Estos resultados muestran que para el estimador de la pendiente de \(X2_i\):

• Los estimadores MCO siguen siendo insesgados en presencia de heteroscedasticidad.
• El error estándar de los coeficientes es más grande en presencia de heteroscedasticidad.

Ahora, comparemos los resultados para la pendiente que acompaña a \(X3_i\).

round(apply(X3.estcoef,2,mean),2)

##   X3.cf.homo X3.cf.hetero 
##            0            0

round(apply(X3.estcoef,2,sd), 2)

##   X3.cf.homo X3.cf.hetero 
##         0.15         0.24

Los resultados son similares para el estimador de la pendiente de la variable que no debería estar en el modelo. Finalmente, puedes inspeccionar los histogramas de la distribución empírica de los coeficientes estimados en los dos escenarios (Ver Figura 9.3).

## TableGrob (2 x 2) "arrange": 4 grobs
##   z     cells    name           grob
## 1 1 (1-1,1-1) arrange gtable[layout]
## 2 2 (1-1,2-2) arrange gtable[layout]
## 3 3 (2-2,1-1) arrange gtable[layout]
## 4 4 (2-2,2-2) arrange gtable[layout]

Figura 9.3: Distribución muestral de los estimadores bajo homoscedasticidad y heteroscedasticidad (en azul se presenta la media de los coeficientes estimados)

Fuente: elaboración propia.

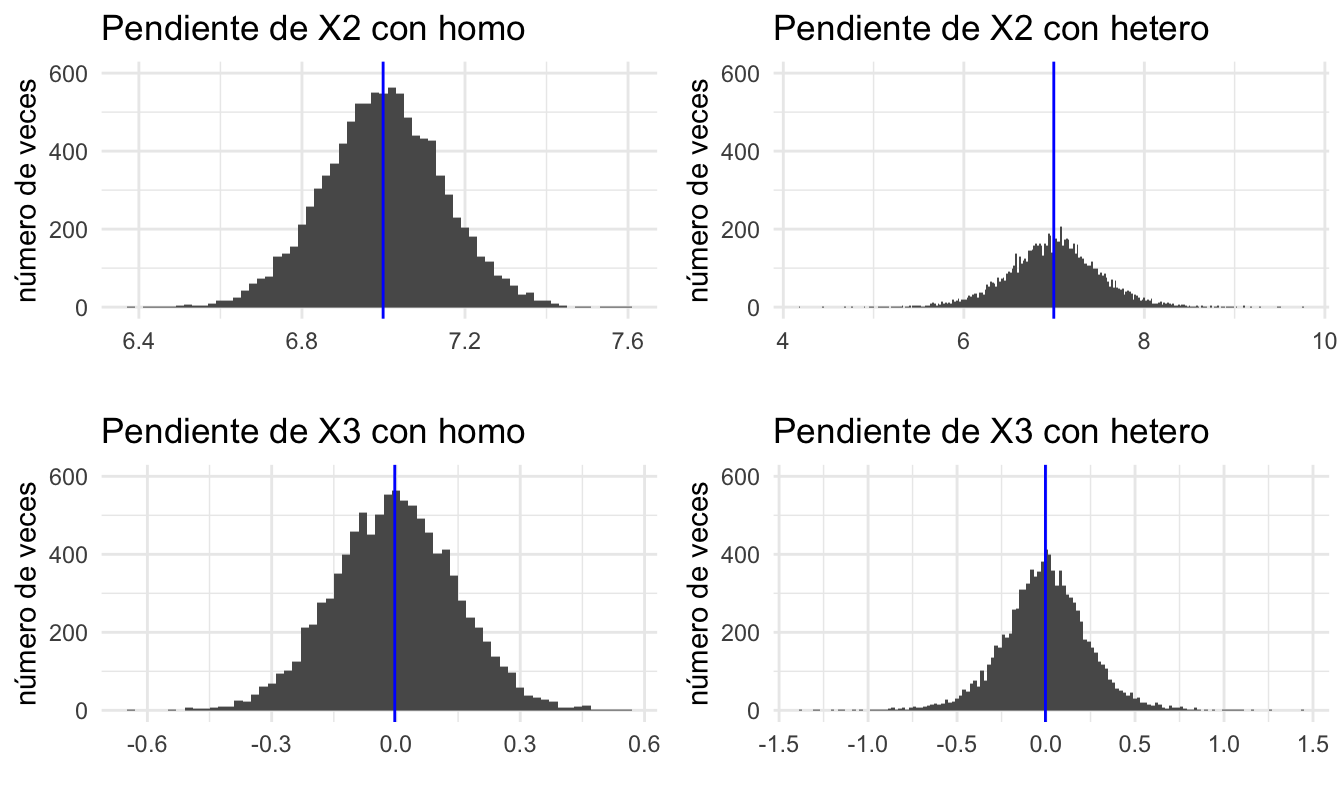
En este capítulo estudiaremos cómo detectar si se viola el supuesto de varianza constante del error y de encontrar el problema cómo resolverlo.

9.2 Pruebas para la detección de heteroscedasticidad

En general, una buena práctica cuando se estiman modelos econométricos es emplear gráficos qué permitan intuir que está ocurriendo con los residuos estimados. Esto permite intuir si existen síntomas de la presencia de heteroscedasticidad. Obviamente, los gráficos no proveen evidencia contundente para concluir, pero sí proveen la intuición necesaria para iniciar las pruebas formales.

Pero, el científico de datos se puede enfrentar a la necesidad de estimar muchos modelos o tener muchas iteraciones entre modelos y tener que automatizar el proceso. En esos escenarios el análisis gráfico no es una opción. No obstante, para ganar un poco de la intuición del problema.

Regresando al análisis gráfico, dado que la heteroscedasticidad implica una variabilidad no constante del error, entonces lo más adecuado será graficar el vector de errores (\(\varepsilon\)). Lastimosamente, este vector no es observable, pero la mejor aproximación que tenemos para conocer ese vector es el error estimado (\(\hat \varepsilon\)). Así, para intuir gráficamente la presencia de heteroscedasticidad se deben visualizar los residuos del modelo estimado. Las visualizaciones más empleadas son gráficos de dispersión de:

1. Los errores estimados versus las observaciones (\(\hat \varepsilon_i\) vs \(i = 1,2,...n\))
2. Los errores estimados versus cada una de las variables explicativas (\(\hat \varepsilon_i\) vs cada una de las columnas de \(\bf X\))

Estas visualizaciones de los errores estimados se emplean para explorar algún tipo de regularidad. En la Figura 9.4 se presentan tipos de patrones que se pueden observar en los residuales estimados que pueden sugerir presencia de heteroscedasticidad.

Figura 9.4: Posibles patrones de comportamiento de los residuales que sugieren heteroscedasticidad

Fuente: elaboración propia.

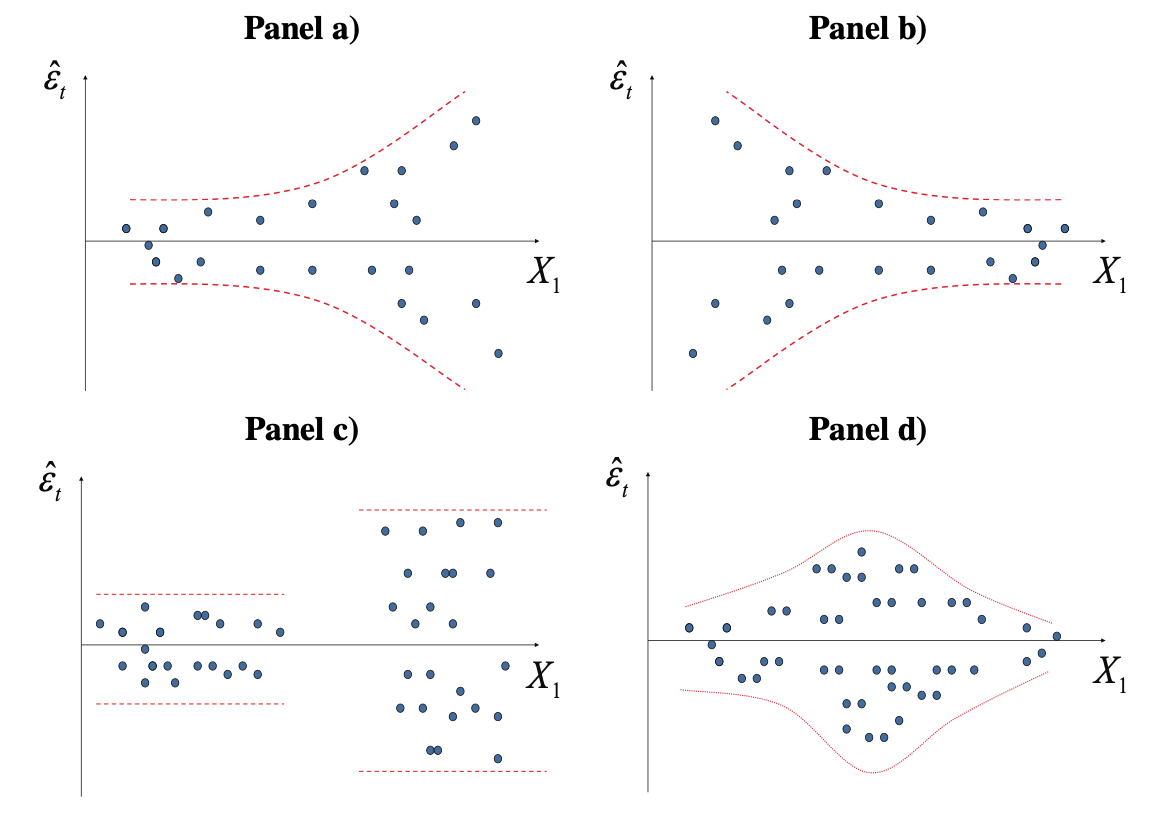
En el panel a) de la Figura 9.4 observamos que los residuos se vuelven más grandes a medida que la variable dependiente crece. En este caso la dispersión con respecto a la media (cero) crece a medida que la variable explicativa crece y esto sucede de manera exponencial. Por tanto, existe heteroscedasticidad que podría ser del tipo \(\sigma _i^2 = {X_{1i}}{\sigma ^2}\). En el panel b) el comportamiento de la varianza es opuesto al presentado en el panel a), heteroscedasticidad que podría ser del tipo \(\sigma _i^2 = \frac{1}{{{X_{1i}}}}{\sigma ^2}\). En el panel c) claramente existen dos grupos de datos; los de varianza grande y los de baja varianza. Por último, en el panel d) los residuos son menores para las mediciones grandes y pequeñas pero crecen en los valores intermedios de la misma. En los cuatro casos hay síntomas de heteroscedasticidad.

Antes de entrar a considerar las pruebas formales, es importante aclarar que la heteroscedasticidad implica una varianza diferente del error para al menos una observación, así existen muchas formas de heteroscedastidad. Es decir, la heteroscedasticidad puede depender de una variable explicativa, de una variable que no se incluye en el modelo o de cualquier función de las observaciones. Esto hace difícil la tarea de identificar el problema con gráficos y con pruebas.

En la práctica los científicos de datos enfrentan comúnmente problemas en los que los modelos incluyen muchas variables explicativas, así realizar un análisis gráfico puede ser un trabajo que tome mucho tiempo y no genere mucha intuición sobre este problema. En esas situaciones, el análisis gráfico puede ser inútil.

A continuación, consideraremos dos pruebas de heteroscedasticidad, cada una diseñada para detectar diferentes formas de heteroscedasticidad. En los dos casos la hipótesis nula de estas pruebas es la presencia de homoscedasticidad \({H_0}:\sigma _i^2 = {\sigma ^2};\: \forall i\) versus la hipótesis alterna de que existe algún tipo de heteroscedasticidad.

9.3 Prueba de Breusch-Pagan

Esta prueba, permite la posibilidad de determinar si más de una variable causa el problema de heteroscedasticidad.

Breusch & Pagan (1979) diseñaron una prueba que permite detectar si existe una relación entre la varianza del error y un grupo de variables (recogidas en un vector \(Z\)). El tipo de relación de esta prueba no está suscrita a algún tipo de relación funcional. En este caso, la prueba está diseñada para detectar la heteroscedasticidad de la forma \(\sigma _i^2 = f\left( {\gamma + \delta {Z_i}} \right)\). Donde \({Z_{i\left( {g \times 1} \right)}}\) es un grupo de \(g\) variables que afectan a la varianza que se organizan en forma vectorial y \({\delta _{\left( {1 \times g} \right)}}\) corresponde a un vector de constantes.

Por ejemplo, supongamos que el científico de datos cree que el problema de heteroscedasticidad está siendo causado por las variables \(W_i\) y \(V_i\). En ese caso tendremos que \({Z_{i\left( {2 \times 1} \right)}} = {\left[ {{W_i},{V_i}} \right]^T}\) y \({\delta _{\left( {1 \times 2} \right)}} = \left[ {{\delta _1},{\delta _2}} \right]\). Por tanto, \(\sigma _i^2 = f\left( {\gamma + {\delta _1}{W_i} + {\delta _2}{V_i}} \right)\).

Recapitulando, la prueba de Breusch-Pagan implica las siguientes hipótesis nula y alterna: \[\begin{equation*} \begin{array}{c} {H_0}:\sigma _i^2 = {\sigma ^2}{\rm{; }} \: \: \: \forall i \\ {H_A}:\sigma _i^2 = f\left( {\gamma + \delta {Z_i}} \right) \\ \end{array} \end{equation*}\]

Los pasos para efectuar esta prueba son los siguientes:

1. Correr el modelo original \(Y = X\beta + \varepsilon\) y encuentra la serie de los residuos \(\hat \varepsilon\).
2. Calcule⁹⁶ \({\hat \sigma ^2} = \frac{{{{\hat \varepsilon }^T}\hat \varepsilon }}{n} = \frac{{\sum\limits_{i = 1}^n {\hat \varepsilon_i^2} }}{n}\).
   
3. Posteriormente, estimar la siguiente regresión auxiliar: \(\frac{{\hat \varepsilon_i^2}}{{{{\hat \sigma }^2}}} = \gamma + \delta {Z_i} + {\mu _i}\).
4. Calcular la suma de los cuadrados de la regresión auxiliar (\(SSR=SST-SSE\)).
5. Calcular el estadístico \(BP = \frac{{SSR}}{2}\).

Breusch & Pagan (1979) demostraron que el estadístico \(BP\) sigue una distribución Chi-cuadrado con \(g\) grados de libertad (\(\chi _g^2\)), bajo el supuesto de que los errores se distribuyen normalmente. Por tanto, se rechazará la hipótesis nula de homoscedasticidad a favor de una heteroscedasticidad de la forma \(\sigma _i^2 = f\left( {\gamma + \delta {Z_i}} \right)\) si el estadístico \(BP\) es mayor que \(\chi _{g,\alpha }^2\), con un nivel de confianza del (\(1-\alpha\))%.

Sin embargo, se ha documentado mucho que esta prueba no funciona bien cuando el supuesto de normalidad no se cumple (Ver por ejemplo Koenker (1981)). Koenker (1981) propone una modificación de la prueba BP que implica transformación de los residuos. Esta modificación se conoce como la versión studentizada de la prueba BP.

9.4 Prueba de White

White (1980) desarrolló una prueba más general que las anteriores, con la ventaja de no requerir que ordenemos los datos en diferentes grupos, ni tampoco depende de que los errores se distribuyan normalmente. Esta prueba implica las siguientes hipótesis nula y alterna: \[\begin{equation} \begin{array}{c} {H_0}:\sigma _i^2 = {\sigma ^2}; \: \: \: \forall i \\ {H_A}:No \: \:{H_0} \\ \end{array} \tag{9.1} \end{equation}\] Los pasos para efectuar esta prueba son los siguientes:

1. Correr el modelo original \({\bf y} = {\bf X}\beta + \varepsilon\) y encontrar la serie de los residuos \(\hat \varepsilon\).
2. Correr la siguiente regresión auxiliar: \(\hat \varepsilon_i^2 = \gamma + \sum\limits_{m = 1}^k {\sum\limits_{j = 1}^k {{\delta _s}{X_{mi}}} } {X_{ji}} + {\mu _i}\). Por ejemplo, si el modelo original es \({Y_i} = {\beta _1} + {\beta _2}{X_{2i}} + {\beta _3}{X_{3i}} + {\varepsilon_i}\), entonces el modelo para la regresión auxiliar será⁹⁷: \(\hat \varepsilon_i^2 = \gamma + {\delta _1}{X_{2i}} + {\delta _2}{X_{3i}} + {\delta _3}X_{2i}^2 + {\delta _4}X_{3i}^2 + {\delta _5}{X_{2i}}{X_{3i}} + {\vartheta _i}\).
3. Calcular el \(R^2\) de la regresión auxiliar.
4. Calcular el estadístico de White \(W_{a} = n \times R^2\).

White (1980) demostró que su estadístico \({W_a}\) sigue una distribución Chi-cuadrado con un número de grados de libertad igual al número de regresores que se emplean en la regresión auxiliar (\(g\)). Por tanto, se rechazará la hipótesis nula de no heteroscedasticidad con un nivel de confianza de (\(1-\alpha\))%, cuando el estadístico de esta prueba sea mayor que \(\chi _{g,\alpha }^2\).

9.5 Solución a la heteroscedasticidad

En la sección pasada se discutió cómo detectar la presencia de heteroscedasticidad; pero, ¿qué hacer si ésta, está presente en un modelo de regresión? A continuación, existen dos soluciones que se emplean comúnmente en la estadística y econometría tradicional para solucionar el problema. La primera solución es tratar de resolver de raíz el problema modificando la muestra. Este método se conoce como el método de Mínimos Cuadrados Ponderados (MCP)⁹⁸ que hace parte de la familia de los Mínimos Cuadrados Generalizados (MCG). Esta aproximación implica conocer exactamente cómo es la heteroscedasticidad; algo que típicamente es difícil para el científico de datos.

La segunda opción implica solucionar los síntomas de la heteroscedasticidad, tratando de estimar de manera consistente⁹⁹ la matriz de varianza y covarianzas de los coeficientes estimados. Esto permite corregir los errores estándar de los coeficientes, y de esta manera los t calculados serán recalculados y, por tanto, los valores p son diferentes.

9.6 Estimación consistente en presencia de heteroscedasticidad de los errores estándar.

Es muy probable que en la práctica no podamos encontrar la forma exacta de la heteroscedasticidad y por tanto no podremos “corregir” la muestra, de tal manera que la heteroscedasticidad desaparezca, tal como lo hace el método de MCP. Para dar solución a esta dificultad, White (1980) ideó una forma de corregir el estimador que tiene el problema y no la muestra.

En especial, White (1980) mostró que es posible aún encontrar un estimador apropiado para la matriz de varianzas y covarianzas de los \(\beta\)’s obtenidos por MCO¹⁰⁰. Recordemos que en presencia de heteroscedasticidad, la varianza de los coeficientes tiene la siguiente estructura: \[\begin{equation*} Var\left[ {\hat \beta } \right] = {\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}{{\bf{X}}^{\bf{T}}}\Omega {\bf{X}}{\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}} \end{equation*}\] White (1980) sugiere usar el siguiente estimador consistente para la matriz de varianzas y covarianzas de los \(\beta's\) obtenidos por MCO: \[\begin{equation*} Est.Var\left[ {\hat \beta } \right] = n{\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}{S_0}{\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}} \end{equation*}\] donde: \[\begin{equation*} {S_0} = \frac{1}{n}\sum\limits_{i = 1}^n {\hat \varepsilon_i^2{x_i}x_i^T} \quad \: \: x_i^T = \left( {\begin{array}{*{20}{c}} 1 & {{x_{1i}}} & {{x_{2i}}} & \ldots & {{x_{ki}}} \\ \end{array}} \right) \end{equation*}\]

Esa matriz de varianzas y covarianzas deberá ser empleada para calcular los estadísticos de las pruebas de hipótesis tanto individuales como conjuntas. De esta manera, el problema del sesgo en la matriz de varianzas y covarianzas es solucionado. De hecho, White (1980) demostró que ese estimador es consistente; es decir, es sesgado en muestras pequeñas (y por tanto no funciona) pero insesgado en muestras grandes (y por tanto funciona bien en muestras grandes). Por esta razón este estimador (y otros similares) es conocido como estimador H.C. (heteroskedasticity consistent). Es importante mencionar, que esto no hace que al emplear esta solución se obtenga un estimador MELI. La varianza del estimador MCO sigue siendo más grande que por ejemplo los del estimador MCG.

Por otro lado, Davidson, Russell and MacKinnon (1993) y Cribari-Neto (2004) propusieron modificaciones a la propuesta de White (1980). Es decir, existen varios estimadores H.C. disponibles. El estimador de White para la matriz de varianzas y covarianzas de \(\hat \beta\) se tiene:

\[\begin{equation*} \frac{1} {n}\left( {\frac{{{\mathbf{X}}^T {\mathbf{X}}}} {n}} \right)^{ - 1} \left( {\frac{1} {n}\sum\limits_{i = 1}^n {\omega_i {\mathbf{x}}_i {\mathbf{x}}_i^T } } \right)\left( {\frac{{{\mathbf{X}}^T {\mathbf{X}}}} {n}} \right)^{ - 1} \end{equation*}\] La diferencia entre los métodos H.C. propuestos están en \(\omega_i\) (ponderación de los datos). Por ejemplo,

• White (1980) propone \(\omega_i = e_i^2\) (A este método se le conoce como HC0).

• Davidson, Russell and MacKinnon (1993) proponen : \(\omega_i =\frac{n}{{n - k}}e_i^2\) (HC1).

• Davidson, Russell and MacKinnon (1993) también proponen otro estimador: \(\omega_i = \frac{e_i^2 }{1 - p_{ii} }\) (HC2), donde \(p_{ii}\) es el elemento \(i\) de la matriz de proyecciones conocida como \(\mathbf{P}\) gorro.

• Davidson, Russell and MacKinnon (1993) sugieren un tercer estimador: \(\omega_i =\frac{{e_i^2 }}{{\left( {1 - p_{ii} } \right)^2 }}\) (HC3).

• Cribari-Neto (2004) proponen: \(\omega_i = \frac{{e_i^2 }}{{\left( {1 - p_{ii} } \right)^{\delta_i } }}\) (HC4), donde \(\delta_i = \min \left\{ {4,{{p_{ii}/ \bar p}}} \right\}\) y \(\bar p = \frac{{\sum_{i = 1}^n {p_{ii} } }}{n}\).

Davidson, Russell and MacKinnon (1993) sugerían nunca usar White (1980) (HC0) pues podemos encontrar un mejor estimador. En esa misma dirección, J. Long & Ervin (2000) encontraron con simulaciones de Monte Carlo que HC3 se comporta mejor en muestras pequeñas y grandes. Cribari-Neto (2004) mostró que HC4 se comporta mejor en muestras pequeñas, especialmente si hay observaciones influyentes.

Por otro lado, también es importante reconocer que al emplear un estimador H.C. también debemos modificar nuestras pruebas conjuntas empleando la correspondiente matriz H.C.

Por ejemplo, la prueba de Wald para una restricción de la forma \({\mathbf{R}}\beta = {\mathbf{q}}\) será: \[\begin{equation*} W = \left( {{\mathbf{R}\hat \beta}} \right)^T \left[ {{\mathbf{R}}\left( {{\text{Est}}{\text{.Asy}}{\text{.}}Var\left[ {\hat \beta } \right]} \right){\mathbf{R}}^T } \right]^{ - 1} \left( {{\mathbf{R} \hat \beta}} \right) \end{equation*}\]

9.7 Práctica en R

Continuaremos con la pregunta de negocio que discutimos en el Capítulo anterior (Ver sección 8.5). Recordemos que en este caso el gerente del hospital de nivel tres “SALUD PARA LOS COLOMBIANOS”, ubicado en la ciudad de Bogotá, tenía la siguiente pregunta de negocio: ¿existe o no una brecha salarial entre hombres y mujeres? Los datos se encuentran disponibles en el archivo DatosMultiColinealidad.csv^[Los datos y la aproximación de esta sección corresponden a Bernat (2004).}. Los datos se pueden descargar de la página web del libro: https://www.icesi.edu.co/editorial/modelo-clasico/.

El modelo que estimamos fue el siguiente: \[\begin{equation} \ln (ih_i) = {\beta_0} + {\beta_1}yedu_i + {\beta_2}exp _i + {\beta_3}exp _i^2 + {\beta_4}{D_i} + {\beta_5}Dexp _i + {\beta_6}Dexp _i^2 + \varepsilon_i \tag{9.2} \end{equation}\] donde, \[\begin{equation*} {\rm{ }}{D_i} = \left\{ {\begin{array}{*{20}{c}} 1 & {\rm{si\: el\: individuo \:} {\textit{$i$}} \rm{\: es \: mujer}} \\ 0 & {o.w.} \\ \end{array}} \right. \end{equation*}\] Además, \(\ln(ih_i)\) representa el logaritmo natural del ingreso por hora del individuo \(i\), \(yedu_i\) y \(exp_i\) denotan los años de educación y de experiencia del individuo \(i\).

Adicionalmente, recuerden que habíamos encontrado un problema de multicolinealidad que decidimos era mejor no resolver. Ahora nuestra tarea será aplicar las diferentes pruebas de heteroscedasticidad y de ser el caso aplicar una solución.

Carga los datos y estima el modelo de nuevo guardando los resultados en un objeto res1.

9.8 Análisis gráfico de los residuos

Como se mencionó anteriormente, una práctica común para detectar intuitivamente problemas de heteroscedasticidad en el término de error es emplear gráficas de dispersión de los errores estimados (\(\hat \varepsilon\)) y de las variables independientes, al igual que los errores estimados y el valor estimado de la variable dependiente. Algunos autores también sugieren emplear gráficos de dispersión del cuadrado de los residuos (\({\hat \varepsilon ^2}\)) y las variables explicativas. Estos gráficos son empleados para determinar la existencia de algún patrón en la variabilidad del error. En este caso sólo graficaremos los errores contra las variables explicatorias \(yedu_i\), \(exp_i\) y \(exp_i^2\) (Pero tu puedes efectuar todos los otros gráficos). Recuerden que es muy probable que este análisis gráfico no sea útil con las cantidades de variables explicativas que trabajan los científicos de datos.

Extraigamos los residuales del objeto de clase lm con la función resid() del paquete central de R. Esta función solo requiere como argumento un objeto de clase lm. Además, guardemos los residuales en el objeto e.

e <-resid(res1)

El correspondiente modelo estimado se reportó en el capítulo anterior (Ver Cuadro 8.1). Pero noten que esos resultados no son interesantes hasta que estemos seguros que no existe un problema de heteroscedasticidad. Ahora grafiquemos los residuos versus las variables explicativas del modelo (Ver Figura 9.5).

par(mfrow=c(2,2))
plot(datos$yedu, e)
plot(datos$exp, e)
plot(datos$exp^2, e)
plot(as.numeric(datos$sexo == "mujer"), e)

Figura 9.5: Gráfico de residuales versus variables explicativas

Fuente: elaboración propia.

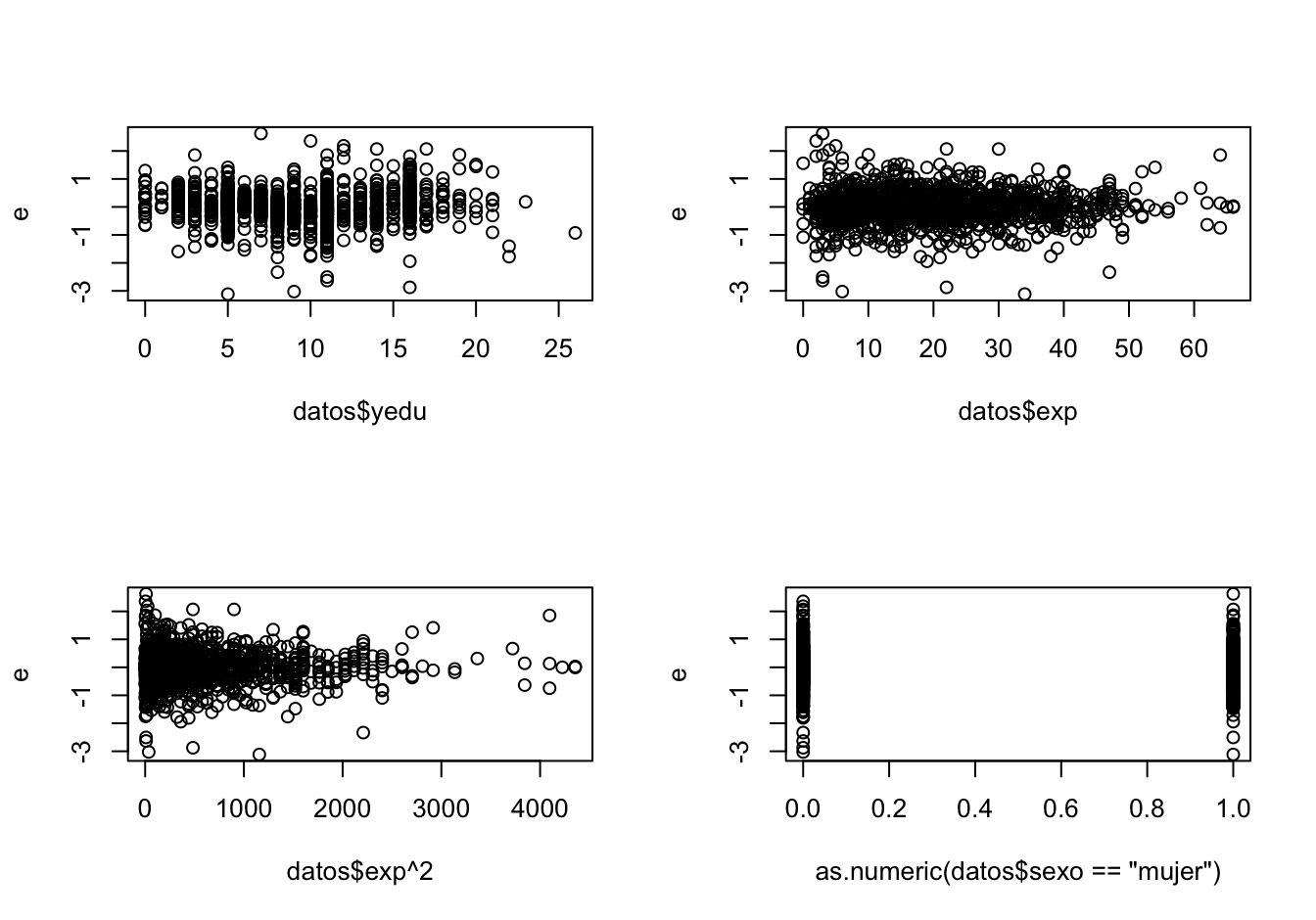
En el gráfico no es posible apreciar una relación clara entre la variabilidad de los errores y los años de educación al igual que con la variable sexo. Con los años de experiencia parece existir menos dispersión a medida que los años de experiencia aumentan. Pero este fenómeno se hace evidente cuando se grafican los residuos versus los años de experiencia al cuadrado. Se observa claramente que la dispersión de los residuos disminuye a medida que se incrementa el cuadrado de la experiencia. Este es un síntoma de heteroscedasticidad.

9.9 Pruebas de heteroscedasticidad

9.9.0.1 Prueba de Breusch-Pagan

Hay muchas funciones que permiten calcular esta prueba en R. Por ejemplo, existe la función bptest() del paquete lmtest (Zeileis & Hothorn, 2002) que nos da la opción de calcular la versión studentizada de la prueba propuesta por Koenker (1981) para el caso en que los residuos no sigan una distribución normal. Otra función con unas opciones muy útiles es ols_test_breusch_pagan() del paquete olsrr (Hebbali, 2020). Esta última función no permite calcular la versión studentizada de la prueba pero permite hacer simultáneamente muchas pruebas de Breusch-Pagan y corrige los valores p para tener en cuenta las múltiples pruebas que se pueden realizar al mismo tiempo. Las correcciones que incluye esta función son las de Bonferroni, Sidak y Holm.

Empecemos empleando la función bptest() del paquete lmtest. Esta función tiene tres argumentos importantes, uno de ellos indispensable bptest(formula, varformula = NULL, studentize = TRUE, data = list())

donde:

• formula: fórmula del modelo de regresión o un objeto de clase lm.
• varformula: una fórmula que incluya las posibles variables explicativas de la varianza. Por defecto se toman las mismas variables explicativas que en el modelo de regresión principal.
• studentize: permite determinar si se empleará la versión studentizada de la prueba o no. El valor por defecto es studentize = “TRUE”. Es decir, si no se especifica este argumento se calculará la versión studentizada.
  • data: si se emplea una fórmula para la varianza, este argumento es obligatorio y tendrá que contener el data.frame donde se encuentran las variables que se emplean para explicar la varianza.

De esta manera, la prueba de Breush-Pagan cuya hipótesis alterna es que todas las variables del modelo causan el problema de heteroscedasticidad se puede calcular con el siguiente código:

library(lmtest)
bptest(res1, studentize = FALSE)

## 
##  Breusch-Pagan test
## 
## data:  res1
## BP = 49.546, df = 6, p-value = 5.798e-09

En este caso se puede rechazar la nula de homoscedasticidad en favor de la alterna. Es decir, la varianza es función de todas las variables. En otras palabras, existe un problema de heteroscedasticidad.

Si queremos ver si es la variable exp la que causa el problema de heteroscedasticidad, podemos hacerlo fácilmente, empleando el siguiente código.

bptest(res1, ~ exp, studentize = FALSE, data = datos)

## 
##  Breusch-Pagan test
## 
## data:  res1
## BP = 2.3968, df = 1, p-value = 0.1216

En este caso la hipótesis nula de homoscedasticidad no es rechazada y, por tanto, se concluiría que existe homoscedasticidad (por lo menos no existe heteroscedasticidad causada únicamente por la variable exp), contrario a como lo intuimos de los gráficos. Noten que esto llama la atención a la necesidad de hacer múltiples pruebas con hipótesis alternas diferentes (por lo menos para cada variable y el total de estas).

La función ols_test_breusch_pagan() del paquete olsrr, permite probar al mismo tiempo si cada una de las variables está causando el problema de heteroscedasticidad o todas al mismo tiempo. Esta función requiere de cuatro argumentos. ols_test_breusch_pagan(model, rhs, multiple, p.adju)

donde:

• model: El objeto de clase lm al que se le realizará la prueba
• rhs: es un valor lógico, si es igual a implica que se emplearán todas las variables explicativas del modelo para hacer las pruebas; si entonces la hipótesis alterna será que la varianza es función de los valores estimados de la variable dependiente (esto comúnmente no tiene mucho sentido).
• multiple: es igual a un valor lógico y permite realizar todas las pruebas en las que la varianza depende de cada una de las variables explicativas y de todas ella (multiple = TRUE).
• p.adj: permite especificar qué tipo de corrección estadística aplicarle al valor p para tener en cuenta que se están realizando múltiples comparaciones al tiempo. Las opciones para este argumento son “none” para ninguna corrección, “bonferroni” para la corrección de Bonferoni, “sidak” para la de Sidak y “holm” para la de Holm.

Por ejemplo, el siguiente código realiza pruebas de Breusch-Pagan para cada una de las variables explicativas y para todas al tiempo, y corrige los respectivos valores p con el método de Bonferroni.

library(olsrr)
ols_test_breusch_pagan(res1, rhs = TRUE, multiple = TRUE,
                       p.adj = 'bonferroni')

## 
##  Breusch Pagan Test for Heteroskedasticity
##  -----------------------------------------
##  Ho: the variance is constant            
##  Ha: the variance is not constant        
## 
##                                  Data                                   
##  -----------------------------------------------------------------------
##  Response : Lnih 
##  Variables: yedu exp I(exp^2) sexomujer exp:sexomujer I(exp^2):sexomujer 
## 
##              Test Summary (Bonferroni p values)            
##  --------------------------------------------------------
##   Variable                 chi2        df         p       
##  --------------------------------------------------------
##   yedu                  23.13058768     1    9.081815e-06 
##   exp                    2.39681316     1    7.294963e-01 
##   I(exp^2)               0.06323815     1    1.000000e+00 
##   sexomujer              3.46086767     1    3.770240e-01 
##   exp:sexomujer          3.96265681     1    2.791214e-01 
##   I(exp^2):sexomujer     1.73988308     1    1.000000e+00 
##  --------------------------------------------------------
##   simultaneous          49.54557532     6    5.797772e-09 
##  --------------------------------------------------------

Los resultados muestran que con un 99% de confianza podemos rechazar la nula de homoscedastidad para todos los casos. Es importante anotar que los estadísticos resultantes no son iguales entre la función bptest() y ols_test_breusch_pagan() dado que esta última no emplea como estadístico de prueba \(BP = \frac{{SSR}}{2}\) sino \(n R^2\). En todo caso los resultados son equivalentes.

Antes de concluir que existe un problema de heteroscedasticidad, es importante estar seguros que el supuesto de normalidad de los errores que requiere esta prueba se cumple. Existen varias pruebas de normalidad como se discute en Alonso & Montenegro (2015), todas tienen la característica de que la hipótesis nula es la normalidad y la alterna es la no normalidad. Las pruebas más comunes de normalidad son Shapiro-Wilk (Shapiro & Francia, 1972), Kolmogorov-Smirnov (Kolmogorov, 1933), Cramer-von Mises (Cramér, 1928) y Anderson-Darling (Anderson & Darling, 1952). Una forma rápida de realizar estas pruebas de normalidad es emplear la función ols_test_normality() del paquete olsrr. La hipótesis nula de estas pruebas de normalidad es que la variable fue generada por una distribución normal, versus la alterna que es otra distribución.

ols_test_normality(res1)

## -----------------------------------------------
##        Test             Statistic       pvalue  
## -----------------------------------------------
## Shapiro-Wilk              0.9583         0.0000 
## Kolmogorov-Smirnov        0.0636         0.0000 
## Cramer-von Mises         174.9537        0.0000 
## Anderson-Darling         12.4223         0.0000 
## -----------------------------------------------

En todos los casos las pruebas de normalidad permiten concluir que los residuos no siguen una distribución normal. Por eso, no son confiables los resultados de la prueba de Breusch-Pagan tradicional. Deberíamos entonces emplear la versión studentizada de la prueba propuesta por Koenker (1981) para el caso en que los residuos no sigan una distribución normal.

bptest(res1, studentize = TRUE)

## 
##  studentized Breusch-Pagan test
## 
## data:  res1
## BP = 18.412, df = 6, p-value = 0.00528

Por lo tanto, los resultados de esta prueba indican que existe un problema de hetereoscedasticidad.

9.9.0.2 Prueba de White

Por último, realicemos la prueba de White¹⁰¹ para contrastar la hipótesis nula de no heteroscedasticidad versus la alterna de heteroscedasticidad se puede calcular empleando la función white() del paquete skedastic (Farrar & University of the Western Cape, 2024). Esta función típicamente incluye los siguientes argumentos: white(mainlm, interactions = FALSE)

donde:

• mainlm: es un objeto de clase lm que contiene la regresión sobre la cual se realizará la prueba.
• interactions: es un valor lógico, si es igual a TRUE se incluyen los términos de interacción; si interactions = FALSE entonces no se incluyen los términos de interacción. Esta última es la opción por defecto. En general es recomendable incluir los términos de interacción (esto comúnmente no tiene mucho sentido).

library(skedastic)

white(res1, interactions = TRUE)

## # A tibble: 1 × 5
##   statistic p.value parameter method       alternative
##       <dbl>   <dbl>     <dbl> <chr>        <chr>      
## 1      37.9  0.0793        27 White's Test greater

En este caso con un 95% de confianza no se puede rechazar la hipótesis nula de homoscedasticidad.

9.10 Solución al problema de heteroscedasticidad con HC

Sumando los resultados de las pruebas anteriores, se puede concluir que existe evidencia de la presencia de heteroscedasticidad. Por tanto, es pertinente solucionar el problema para hacer inferencia.

Como se discutió anteriormente, una forma de solucionar el problema es empleando estimadores consistentes en presencia de heteroscedasticidad para la (H.C.) para la matriz de varianzas y covarianzas. Esto se puede hacer empleando el paquete sandwich (Zeileis, 2004) y la función vcovHC(). Esta función requiere dos argumentos: el objeto de clase lm al que se le quiere corregir la matriz de varianzas y covarianzas y el tipo de corrección que por defecto es la que denominamos HC3 (la propuesta por Davidson, Russell and MacKinnon (1993) y sugerida por Cribari-Neto (2004)).

Para este caso, tenemos que la corrección HC3 se puede estimar de la siguiente manera:

library(sandwich) 
#    HC3 Davidson y MacKinnon (1993) 
vcovHC(res1) 

##                      (Intercept)          yedu           exp      I(exp^2)
## (Intercept)         8.317882e-03 -2.271974e-04 -4.947456e-04  7.713180e-06
## yedu               -2.271974e-04  2.059261e-05  1.825652e-06  1.795725e-08
## exp                -4.947456e-04  1.825652e-06  4.626380e-05 -8.473137e-07
## I(exp^2)            7.713180e-06  1.795725e-08 -8.473137e-07  1.718700e-08
## sexomujer          -5.423997e-03 -3.514125e-05  4.723621e-04 -7.955854e-06
## exp:sexomujer       4.554557e-04  1.742774e-06 -4.609217e-05  8.527277e-07
## I(exp^2):sexomujer -7.815056e-06 -8.851575e-09  8.506639e-07 -1.721951e-08
##                        sexomujer exp:sexomujer I(exp^2):sexomujer
## (Intercept)        -5.423997e-03  4.554557e-04      -7.815056e-06
## yedu               -3.514125e-05  1.742774e-06      -8.851575e-09
## exp                 4.723621e-04 -4.609217e-05       8.506639e-07
## I(exp^2)           -7.955854e-06  8.527277e-07      -1.721951e-08
## sexomujer           9.727628e-03 -8.059566e-04       1.354197e-05
## exp:sexomujer      -8.059566e-04  8.079147e-05      -1.502262e-06
## I(exp^2):sexomujer  1.354197e-05 -1.502262e-06       3.066016e-08

Ahora, como no es muy útil la matriz de varianzas y covarianzas sola, sino más bien los respectivos t individuales y sus correspondientes valores p, podemos emplear la función coeftest() del paquete lmtest para realizar las pruebas individuales. La función coeftest() necesita dos argumentos: coeftest(x, vcov. = NULL)

donde:

• x: es el objeto al que se le realizará la prueba, generalmente de clase lm.
• vcov.: la matriz de varianzas y covarianzas que se quiera emplear. Si no se especifica una matriz de varianzas y covarianzas, entonces se empleara la de los MCO.

Por ejemplo, para este caso podemos ver cómo individualmente, los coeficientes de las variables asociadas a la dummy de sexo no son significativos individualmente.

library(lmtest)
#  HC3 Davidson y MacKinnon (1993) 
coeftest(res1, vcov = (vcovHC(res1))) 

## 
## t test of coefficients:
## 
##                       Estimate  Std. Error t value  Pr(>|t|)    
## (Intercept)         5.8557e+00  9.1202e-02 64.2056 < 2.2e-16 ***
## yedu                1.3064e-01  4.5379e-03 28.7882 < 2.2e-16 ***
## exp                 3.3948e-02  6.8017e-03  4.9911 6.754e-07 ***
## I(exp^2)           -2.9550e-04  1.3110e-04 -2.2540   0.02435 *  
## sexomujer          -1.1666e-01  9.8629e-02 -1.1828   0.23707    
## exp:sexomujer      -3.9387e-03  8.9884e-03 -0.4382   0.66131    
## I(exp^2):sexomujer  5.3015e-05  1.7510e-04  0.3028   0.76211    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Estos resultados comparados con la estimación MCO se reportan en el Cuadro 9.1.

Cuadro 9.1: Modelo estimado por MCO y corrección HC

	MCO	HC3
(Intercept)	5.86***	5.86***
	(0.08)	(0.09)
yedu	0.13***	0.13***
	(0.00)	(0.00)
exp	0.03***	0.03***
	(0.01)	(0.01)
exp^2	-0.00**	-0.00*
	(0.00)	(0.00)
sexomujer	-0.12	-0.12
	(0.08)	(0.10)
exp:sexomujer	-0.00	-0.00
	(0.01)	(0.01)
exp^2:sexomujer	0.00	0.00
	(0.00)	(0.00)
R2	0.45	0.45
Adj. R2	0.45	0.45
Num. obs.	1415	1415
***p < 0.001; **p < 0.01; *p < 0.05

A manera de ejemplo se muestra las otras posibles correcciones.

#    White (1980)
coeftest(res1, vcov = (vcovHC(res1, "HC0"))) 

## 
## t test of coefficients:
## 
##                       Estimate  Std. Error t value  Pr(>|t|)    
## (Intercept)         5.8557e+00  9.0230e-02 64.8974 < 2.2e-16 ***
## yedu                1.3064e-01  4.5104e-03 28.9636 < 2.2e-16 ***
## exp                 3.3948e-02  6.6308e-03  5.1197 3.483e-07 ***
## I(exp^2)           -2.9550e-04  1.2605e-04 -2.3443    0.0192 *  
## sexomujer          -1.1666e-01  9.7408e-02 -1.1977    0.2312    
## exp:sexomujer      -3.9387e-03  8.7934e-03 -0.4479    0.6543    
## I(exp^2):sexomujer  5.3015e-05  1.6940e-04  0.3130    0.7544    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

#    Davidson y MacKinnon (1993) 
coeftest(res1, vcov = (vcovHC(res1, "HC1")))

## 
## t test of coefficients:
## 
##                       Estimate  Std. Error t value  Pr(>|t|)    
## (Intercept)         5.8557e+00  9.0454e-02 64.7367 < 2.2e-16 ***
## yedu                1.3064e-01  4.5216e-03 28.8919 < 2.2e-16 ***
## exp                 3.3948e-02  6.6473e-03  5.1070 3.721e-07 ***
## I(exp^2)           -2.9550e-04  1.2637e-04 -2.3385    0.0195 *  
## sexomujer          -1.1666e-01  9.7650e-02 -1.1947    0.2324    
## exp:sexomujer      -3.9387e-03  8.8152e-03 -0.4468    0.6551    
## I(exp^2):sexomujer  5.3015e-05  1.6982e-04  0.3122    0.7549    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

#    Davidson y MacKinnon (1993)
coeftest(res1, vcov = (vcovHC(res1, "HC2"))) 

## 
## t test of coefficients:
## 
##                       Estimate  Std. Error t value  Pr(>|t|)    
## (Intercept)         5.8557e+00  9.0708e-02 64.5556 < 2.2e-16 ***
## yedu                1.3064e-01  4.5241e-03 28.8759 < 2.2e-16 ***
## exp                 3.3948e-02  6.7141e-03  5.0562 4.839e-07 ***
## I(exp^2)           -2.9550e-04  1.2851e-04 -2.2994   0.02163 *  
## sexomujer          -1.1666e-01  9.8006e-02 -1.1904   0.23411    
## exp:sexomujer      -3.9387e-03  8.8884e-03 -0.4431   0.65774    
## I(exp^2):sexomujer  5.3015e-05  1.7217e-04  0.3079   0.75819    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

#    Cribari-Neto (2004) 
coeftest(res1, vcov = (vcovHC(res1, "HC4"))) 

## 
## t test of coefficients:
## 
##                       Estimate  Std. Error t value  Pr(>|t|)    
## (Intercept)         5.8557e+00  9.1595e-02 63.9306 < 2.2e-16 ***
## yedu                1.3064e-01  4.5321e-03 28.8250 < 2.2e-16 ***
## exp                 3.3948e-02  6.9554e-03  4.8808 1.177e-06 ***
## I(exp^2)           -2.9550e-04  1.3620e-04 -2.1697    0.0302 *  
## sexomujer          -1.1666e-01  9.9245e-02 -1.1755    0.2400    
## exp:sexomujer      -3.9387e-03  9.1539e-03 -0.4303    0.6671    
## I(exp^2):sexomujer  5.3015e-05  1.8070e-04  0.2934    0.7693    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

En este caso se puede observar que los resultados son robustos a la aproximación que se emplee. En todo caso parece ser mejor emplear el HC3 de acuerdo a las simulaciones de Monte Carlo realizadas por J. Long & Ervin (2000).

Ahora miremos si conjuntamente todos los coeficientes que acompañan a las dummy son cero o no con la corrección de heteroscedasticidad. Eso lo podemos hacer de manera muy fácil dado que todas las funciones estudiadas previamente soportan la inclusión de una matriz de varianzas y covarianzas H.C. Por ejemplo,

library(AER)
res2 <-  lm(Lnih ~ yedu + exp + I(exp^2) , datos)

  waldtest(res2, res1, vcov = vcovHC( res1))  

## Wald test
## 
## Model 1: Lnih ~ yedu + exp + I(exp^2)
## Model 2: Lnih ~ yedu + exp + I(exp^2) + sexo + sexo * exp + sexo * I(exp^2)
##   Res.Df Df     F    Pr(>F)    
## 1   1411                       
## 2   1408  3 10.15 1.293e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Los resultados muestran que se puede rechazar la hipótesis nula de que el modelo restringido es mejor que no restringido. Es decir, al menos uno de los coeficientes asociados a la dummy de sexo es significativo. Es decir, sí existe diferencia en como se trata a los hombres y a las mujeres.

9.11 Ejercicios

Las respuestas a estos ejercicios se encuentran en la sección 16.5.

9.11.1 Similación de Monte Carlo

Realice un experimento de Monte Carlo similar al que se realiza en la Introducción de este Capítulo. En este caso nos interesa conocer cuál es la proporción de veces que se rechaza la hipótesis nula de las pruebas individuales para las dos pendientes con los estimadores MCO sin heteroscedasticidad, los estimadores MCO con heteroscedasticidad y la corrección HC3 en parecencia de heteroscedasticidad. Realice el experimento para muestras de tamaño 20, 50, 200 y 1000. ¿Qué puedes concluir?

9.12 Anexos

9.13 Demostración de la insesgadez de los estimadores en presencia de heteroscedasticidad

En presencia de heteroscedasticidad los estimadores MCO siguen siendo insesgados. Esta afirmación se puede demostrar fácilmente. Consideremos un modelo lineal con un término de error heteroscedástico y no autocorrelación. Es decir, \[\begin{equation*} {\bf{y}} = {\bf{X}}\beta + \varepsilon \end{equation*}\] Donde \(E\left[ {{\varepsilon _t}} \right] = 0\), \(Var\left[ {{\varepsilon _t}} \right] = \sigma _\varepsilon ^2\) y \(E\left[ {{\varepsilon_i}{\varepsilon _j}} \right] = 0\), \(\forall i \ne j\). Ahora determinemos si \(\hat \beta = {\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}{{\bf{X}}^{\bf{T}}}{\bf{y}}\) sigue siendo insesgado o no. Así, \[\begin{equation*} E\left[ {\hat \beta } \right] = E\left[ {{{\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)}^{ - 1}}{{\bf{X}}^{\bf{T}}}{\bf{y}}} \right] = {\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}{{\bf{X}}^{\bf{T}}}E\left[ {\bf{y}} \right] \end{equation*}\] \[\begin{equation*} E\left[ {\hat \beta } \right] = {\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}{{\bf{X}}^{\bf{T}}}E\left[ {{\bf{X}}\beta + \varepsilon } \right] = {\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}{{\bf{X}}^{\bf{T}}}{\bf{X}}\beta + {\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}{{\bf{X}}^{\bf{T}}}E\left[ \varepsilon \right] \end{equation*}\] \[\begin{equation*} E\left[ {\hat \beta } \right] = {\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}{{\bf{X}}^{\bf{T}}}{\bf{X}}\beta = I \bullet \beta \end{equation*}\] \[\begin{equation*} E\left[ {\hat \beta } \right] = \beta \end{equation*}\]

9.14 Demostración del sesgo de la matriz de varianzas y covarianzas en presencia de heteroscedasticidad

En presencia de heteroscedasticidad el estimador de la matriz de varianzas y covarianzas de MCO (\(\widehat{Var\left[ {\hat \beta } \right]} = s^2 \left( {{\bf{X}}^{\bf T} {\bf{X}}} \right)\)) es sesgado. Es más, el estimador MCO para los coeficientes (\(\hat \beta = \left( {{\bf{X}}^{\bf T} {\bf{X}}} \right)^{ - 1} {\bf{X}}^{\bf T} {\bf{y}}\)) no es eficiente; es decir no tiene la mínima varianza posible. Esta afirmación se puede demostrar fácilmente.

Continuando con el modelo considerado en el Anexo anterior, en este caso tenemos que: \[\begin{equation*} Var\left[ \varepsilon \right] = E\left[ {\varepsilon ^T \varepsilon } \right] = \Omega = \left[ {\begin{array}{*{20}c} {\sigma _1^2 } & 0 & \ldots & 0 \\ 0 & {\sigma _2^2 } & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & 0 & \ldots & {\sigma _n^2 } \\ \end{array}} \right] \end{equation*}\]

Ahora podemos calcular la varianza de los estimadores MCO. Es decir,

\[\begin{equation*} Var\left[ {\hat \beta } \right] = Var\left[ {\left( {{\bf{X}}^{\bf T} {\bf{X}}} \right)^{ - 1} {\bf{X}}^{\bf T} {\bf{y}}} \right] \end{equation*}\]

Por tanto, tendremos que: \[\begin{equation*} Var\left[ {\hat \beta } \right] = \left( {{\bf{X}}^{\bf T} {\bf{X}}} \right)^{ - 1} {\bf{X}}^{\bf T} Var\left[ {\bf{y}} \right]{\bf{X}}\left( {{\bf{X}}^{\bf T} {\bf{X}}} \right)^{ - 1} \end{equation*}\]

\[\begin{equation*} Var\left[ {\hat \beta } \right] = \left( {{\bf{X}}^{\bf T} {\bf{X}}} \right)^{ - 1} {\bf{X}}^{\bf T} Var\left[ \varepsilon \right]{\bf{X}}\left( {{\bf{X}}^{\bf T} {\bf{X}}} \right)^{ - 1} \end{equation*}\] \[\begin{equation*} Var\left[ {\hat \beta } \right] = \left( {{\bf{X}}^{\bf T} {\bf{X}}} \right)^{ - 1} {\bf{X}}^{\bf T} \Omega {\bf{X}}\left( {{\bf{X}}^{\bf T} {\bf{X}}} \right)^{ - 1} \end{equation*}\]

La varianza no es la mínima posible. Y por otro lado, al emplear el estimador MCO para la matriz de varianzas y covarianzas de los betas (\(\widehat{Var\left[ {\hat \beta } \right]} = s^2 \left( {{\bf{X}}^{\bf T} {\bf{X}}} \right)^{ - 1}\)) en presencia de heteroscedasticidad se obtendrá un estimador cuyo valor esperado no es igual a la varianza real; es decir, el estimador MCO para la matriz de varianzas y covarianzas de los betas será sesgado.

9.15 Solución por mínimos cuadrados ponderados

Si conocemos la varianza de cada uno de los errores es posible utilizar el método de Mínimos Cuadrados Ponderados (MCP) que hace parte de la familia de los Mínimos Cuadrados Generalizados (MCG). La idea de esta solución es muy sencilla, e implica transformar los datos de la muestra de tal forma que el problema desaparezca de la muestra. Por ejemplo, partamos del siguiente modelo: \[\begin{equation} {Y_i} = {\beta _1} + {\beta _2}{X_{2i}} + {\beta _3}{X_{3i}} + \ldots + {\beta _k}{X_{ki}} + {\varepsilon_i} \tag{9.3} \end{equation}\] Con un vector de errores con las siguientes características: \(E\left[ {{\varepsilon_i}} \right] = 0\), \(E\left[ {{\varepsilon_i}{\varepsilon _j}} \right] = 0\), y con una varianza de los errores conocida \(Var\left[ {{\varepsilon_i}} \right] = W_i^2\sigma _i^2\). Si dividimos el modelo por \(W_i\) obtenemos¹⁰²: \[\begin{equation} \frac{{{Y_i}}}{{{W_i}}} = {\beta _1}\frac{1}{{{W_i}}} + {\beta _2}\frac{{{X_{2i}}}}{{{W_i}}} + {\beta _3}\frac{{{X_{3i}}}}{{{W_i}}} + \ldots + {\beta _k}\frac{{{X_{ki}}}}{{{W_i}}} + \frac{{{\varepsilon_i}}}{{{W_i}}} \tag{9.4} \end{equation}\] Note que: \[\begin{equation*} Var\left[ {\frac{{{\varepsilon_i}}}{{{W_i}}}} \right] = \frac{1}{{W_i^2}}Var\left[ {{\varepsilon_i}} \right] = \frac{1}{{W_i^2}}W_i^2{\sigma ^2} = {\sigma ^2} \end{equation*}\] Es decir, ahora cada observación tiene varianza constante y, por lo tanto, el problema de heteroscedasticidad ha sido resuelto, de tal manera que los estimadores MCO para el modelo (9.1) ya son MELI.

El problema práctico de esta aproximación es conocer exactamente la naturaleza de la heteroscedasticidad, por eso en la práctica es aconsejable para los científicos de datos emplear una solución H.C. dados los grandes volúmenes de observaciones que se emplean.

Referencias

Alonso, J. C., & Montenegro, S. (2015). Estudio de Monte Carlo para comparar 8 pruebas de normalidad sobre residuos de mínimos cuadrados ordinarios en presencia de procesos autorregresivos de primer orden. Estudios Gerenciales, 31(In press), 253–265. https://doi.org/10.1016/j.estger.2014.12.003

Anderson, T., & Darling, D. (1952). Asymptotic theory of certain "goodness of fit" criteria based on stochastic processes. The Annals of Mathematical Statistics, 23, 193–212. http://www.jstor.org/stable/2236446

Bernat, L. F. (2004). Diferencias salariales por género en las siete principales áreas metropolitanas colombianas. ¿Evidencia de discriminación? Investigaciones Sobre Género y Desarrollo En Colombia, 1.

Breusch, T. S., & Pagan, A. R. (1979). A simple test for heteroscedasticity and random coefficient variation. Econometrica, 47(5), 1287–1294.

Cramér, H. (1928). On the composition of elementary errors: First paper: Mathematical deductions. Scandinavian Actuarial Journal, 1, 13–74.

Cribari-Neto, F. (2004). Asymptotic inference under heteroskedasticity of unknown form. Computational Statistics & Data Analysis, 45(2), 215–233.

Davidson, Russell and MacKinnon, J. (1993). Estimation and inference in econometrics. Oxford University Press.

Farrar, T. J., & University of the Western Cape. (2024). Skedastic: Handling heteroskedasticity in the linear regression model. https://github.com/tjfarrar/skedastic

Hebbali, A. (2020). Olsrr: Tools for building OLS regression models. https://CRAN.R-project.org/package=olsrr

Koenker, R. (1981). A note on studentizing a test for heteroscedasticity. Journal of Econometrics, 17(1), 107–112.

Kolmogorov, A. N. (1933). Sulla determinazione empirica di una legge di distribuzione. G. Ist. Attuari, 89–91.

Long, J., & Ervin, L. (2000). Using Heteroscedasticity Consistent Standard Errors in the Linear Regression Model. The American Statistician, 54(3), 217–224. http://amstat.tandfonline.com/doi/abs/10.1080/00031305.2000.10474549

Shapiro, S. S., & Francia, R. S. (1972). An approximate analysis of variance test for normality. Journal of the American Statistical Association, 67(337), 215–216. http://amstat.tandfonline.com/doi/abs/10.1080/01621459.1972.10481232

Waldman, D. M. (1983). A note on algebraic equivalence of white’s test and a variation of the godfrey/breusch-pagan test for heteroscedasticity. Economics Letters, 13(2-3), 197–200.

White, H. (1980). A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica, 48(4), 817–838.

Zeileis, A. (2004). Econometric computing with HC and HAC covariance matrix estimators. Journal of Statistical Software, 11(10), 1–17. https://doi.org/10.18637/jss.v011.i10

Zeileis, A., & Hothorn, T. (2002). Diagnostic checking in regression relationships. R News, 2(3), 7–10. https://CRAN.R-project.org/doc/Rnews/

---

93. Es importante aclarar que para las Figuras 9.1 y 9.2 se ha supuesto que los errores siguen una distribución normal para construir una gráfica más intuitiva. Pero este supuesto de normalidad no es necesario en la práctica solo se ha realizado para efectos de la gráfica.↩︎

94. En un anexo al final del capítulo (Ver sección 9.12) se presenta una demostración.↩︎

95. En los anexos al final de este capítulo (Ver sección 9.12) se presenta la demostración.↩︎

96. Noten que esto corresponde al estimador de la varianza del error del Método de Máxima Verosimilitud.↩︎

97. El último término se conoce con el nombre de término cruzado o términos de interacción. En algunas oportunidades cuando el modelo original cuenta con muchas variables explicatórias y/o el número de observaciones no es mucho, puede ocurrir que no existan los grados de libertad necesarios para correr la regresión auxiliar incluyendo los términos cruzados. En esos casos, algunos autores acostumbran correr la regresión auxiliar sin los términos cruzados, si bien esto le resta poder a la prueba. Lo recomendable es incluir los términos de interacción siempre que sea posible, dado que así tiene más poder la prueba White (1980).↩︎

98. En los anexos (Ver sección 9.12 se presenta una breve introducción a este método de solucionar el problema de heteroscedasticidad.↩︎

99. Consistencia en estadística es la propiedad de un estimador de ser insesgado cuando la muestra es grande.↩︎

100. Recuerden que el estimador MCO del vector \(\beta\) sigue siendo insesgado, el problema se presenta en el estimador de la matriz de varianzas y covarianzas.↩︎

101. Waldman (1983) mostró que si las variables en la hipótesis alterna son las mismas que las usadas en la prueba de White, entonces esta prueba es algebraicamente igual a la versión studentizada de Breusch-Pagan (con todas las variables de la regresión auxiliar de White como causantes de la heteroscedasticidad). Es decir, en principio se puede emplear la función bptest() para esta prueba. Pero la mayoría de estas aproximaciones pueden ser engorrosas cuando el modelo incluye muchas variables explicativas y, por tanto, los productos cruzados pueden ser muchos para incluirlos en la fórmula. ↩︎

102. Los \(W_i\) son conocidos como los pesos de ponderación, de ahí el nombre del método.↩︎