3 Análisis de canasta en R
3.1 Introducción
En los Capítulos 1 y 2 estudiamos los fundamentos del MBA (sigla del término en inglés Market Basket Analysis o análisis de canasta). En el Capítulo 2 desarrollamos los conceptos fundamentales y empleamos un ejemplo sencillo para aplicar dichos conceptos. En este Capítulo nos concentraremos en aplicar los conceptos aprendidos en R (R Core Team, 2023). En la práctica, el MBA se realiza con bases de datos que registran millones de transacciones de establecimientos que cuentan con miles de productos (ítems).
El procesamiento de estas grandes bases de datos requiere de herramientas especializadas para su análisis. R es un lenguaje de programación ampliamente utilizado en el análisis de datos y ofrece diversos paquetes y funciones para realizar el MBA. En este Capítulo, exploraremos cómo emplear R y el paquete arules (Hahsler et al., 2011) para realizar un MBA. Con este objetivo, este Capítulo explica cómo preparar los datos para ser procesados (Sección 3.3), cómo emplear el algoritmo Apriori para la selección de reglas interesantes (Sección 3.4) y cómo trabajar con las reglas encontradas (Sección 3.5).
Este Capítulo explica al científico de datos los pasos para generar las reglas de asociación. Además es útil para el analytics translator para entender la lógica que sigue el científico de datos y poder guiar al científico de datos al crear los parámetros de asociación que se esperan visualizar. El analytics translator puede omitir de este Capítulo el detalle del código en R. Es decir, es importante que en el proceso exista un trabajo conjunto entre el científico de datos y el analytics translator para asegurarse de que los resultados sean coherentes con las preguntas del negocio (ver, por ejemplo, la sección 1.1) y las decisiones que se esperan tomar.
En el Capítulo 4 exploraremos cómo visualizar los resultados tanto de las métricas como de las reglas en sí, resultado del MBA. En el Capítulo 5 presentaremos un ejercicio de MBA completo en el que nos concentraremos más en las implicaciones del negocio y una aproximación diferente en la exploración de los datos que tiene sentido en determinados negocios. Pero antes de entrar en esos detalles, aprenderemos, a continuación, las funciones y paquetes de R que permiten hacer un MBA.
3.2 Los datos
Para desarrollar nuestro ejemplo con datos reales, emplearemos un conjunto de datos que contiene transacciones de una empresa de comercio electrónico con sede en el Reino Unido provistas por Online Retail (2015). Dicha empresa se caracteriza por la venta al por menor en línea de regalos para toda ocasión. La base de datos que emplearemos es un subconjunto de todos los datos transaccionales publicados por Online Retail (2015); este subconjunto corresponde únicamente al primer trimestre de 2011 y se descartaron dos variables (la fecha de la transacción y el país de origen de la transacción). Los datos están disponibles en la página web del libro en el archivo Online_Retail_data.csv.
Cada fila del archivo corresponde a un ítem comprado y las variables incluidas en estos datos son las siguientes:
InvoiceNo: Número de la factura que corresponde a un número entero de 6 dígitos. Esta variable permite identificar cuáles ítems (filas) corresponden a la misma transacción (canasta de compra o carrito de compra).SKU: código (número entero de 5 dígitos) del ítem (la referencia del ítem).Description: Descripción del ítem.Quantity: La cantidad comprada del ítem en la transacción.UnitPrice: Precio por unidad del ítem en libras esterlinas.CustomerID: Código (número entero de 5 dígitos) de identificación del cliente.
La base contiene 2981 ítems diferentes. Es decir, la tienda en línea, durante ese período, vendió 2981 diferentes productos (SKU diferentes) que implican un número muy grande de posibles itemsets30 y de reglas31. En total se cuentan con 3777 transacciones de 1777 clientes diferentes. Nota que la base tiene 97449 líneas de datos; cada línea es un ítem vendido cuyos atributos (variables) son SKU, Description, Quantity, UnitPrice y CustomerID.
Para empezar, descarga el archivo Online_Retail_data.csv de la página web del libro, carga los datos y constata que los datos han sido leídos correctamente.
# Cargar los datos
Datos_original <- read.csv("Online_Retail_data.csv", sep = ",")
# Cargar paquete
library(dplyr)
# una miras rápida a los datos cargados
glimpse(Datos_original)## Rows: 97,449
## Columns: 6
## $ InvoiceNo <int> 539993, 539993, 539993, 539993, 539993, 539993, 539993, 53…
## $ SKU <chr> "22386", "21499", "21498", "22379", "20718", "85099B", "20…
## $ Description <chr> "JUMBO BAG PINK POLKADOT", "BLUE POLKADOT WRAP", "RED RETR…
## $ Quantity <int> 10, 25, 25, 5, 10, 10, 6, 12, 6, 8, 6, 6, 6, 12, 12, 8, 4,…
## $ UnitPrice <dbl> 1.95, 0.42, 0.42, 2.10, 1.25, 1.95, 3.25, 1.45, 2.95, 1.95…
## $ CustomerID <int> 13313, 13313, 13313, 13313, 13313, 13313, 13313, 13313, 13…Antes de continuar, carga el paquete arules (Hahsler et al., 2011); si aún no lo has instalado, instálalo.
3.3 Preparación de los datos y análisis preliminar
Para emplear los datos con las funciones del paquete arules, es necesario convertirlos a la clase transactions; esta clase es exclusiva de este paquete. Para convertir un objeto de clase data.frame a transactions, tendremos que agrupar los ítems por el ID de la transacción. Es decir, crear las canastas o “carritos” de compra. Para realizar esta operación de manera rápida debemos seguir dos pasos. Primero, convertir los datos en clase list y el segundo paso es convertir la lista a clase transactions.
Para el primer paso, podemos emplear la función split() de la base de R. Esta función construirá un objeto de clase list 32 con diferentes compartimientos (slots), uno para cada transacción. La función split() tiene los siguientes argumentos:donde:
- x: Es vector o data.frame que contiene los valores a dividir en grupos.
- f: Es un vector de clase factor que definirá cómo agrupar los datos.
En nuestro caso queremos dividir los datos de tal manera que a cada transacción le queden sus correspondientes productos comprados. Es decir, la columna que contiene la descripción de los productos (variable Description) la queremos dividir33 de tal manera que tengamos grupos por factura (InvoiceNo). Esto lo podemos hacer con el siguiente código:
# Separar de los datos
datos_lista = split(Datos_original$Description,
Datos_original$InvoiceNo)
# Chequear la clase del objeto
class(datos_lista)## [1] "list"## $`539993`
## [1] "JUMBO BAG PINK POLKADOT" "BLUE POLKADOT WRAP"
## [3] "RED RETROSPOT WRAP " "RECYCLING BAG RETROSPOT "
## [5] "RED RETROSPOT SHOPPER BAG" "JUMBO BAG RED RETROSPOT"
## [7] "RED RETROSPOT CHILDRENS UMBRELLA" "JAM MAKING SET PRINTED"
## [9] "RECIPE BOX RETROSPOT " "CHILDRENS APRON APPLES DESIGN"
## [11] "PEG BAG APPLES DESIGN" "COFFEE MUG APPLES DESIGN"
## [13] "COFFEE MUG PEARS DESIGN" "WHITE HANGING HEART T-LIGHT HOLDER"
## [15] "SET OF 6 T-LIGHTS EASTER CHICKS" "CAST IRON HOOK GARDEN FORK"
## [17] "LOVE HEART NAPKIN BOX "En el objeto datos_lista tenemos una lista en la que cada compartimiento (slot) corresponde a una transacción y contiene un “carrito” de compra. Por eso se tienen 3777 compartimientos.
Ahora podemos proceder al segundo paso: crear el objeto de clase transactions. Esto lo podemos hacer con la función as(). Esta función (del paquete arules ) solo necesita como argumentos un objeto de clase list y especificar la clase a la que queremos convertir el objeto. En nuestro caso tendremos:
## Warning in asMethod(object): removing duplicated items in transactions## [1] "transactions"
## attr(,"package")
## [1] "arules"Para inspeccionar los datos de clase transactions no podemos emplear la aproximación tradicional. Explora lo que ocurre si empleamos la función head() o simplemente tratamos de imprimir el objeto.
## transactions in sparse format with
## 3777 transactions (rows) and
## 2929 items (columns)## transactions in sparse format with
## 6 transactions (rows) and
## 2929 items (columns)## transactions in sparse format with
## 3777 transactions (rows) and
## 2929 items (columns)Para inspeccionar los datos, podemos emplear la función summary() del paquete arules. Recuerda que cuando tenemos funciones que tienen el mismo nombre en diferentes paquetes, típicamente estas están diseñadas para reaccionar diferente de acuerdo a la clase del objeto que se use en el argumento.
En nuestro caso, el código sería el siguiente:
## transactions as itemMatrix in sparse format with
## 3777 rows (elements/itemsets/transactions) and
## 2929 columns (items) and a density of 0.00866279
##
## most frequent items:
## WHITE HANGING HEART T-LIGHT HOLDER SET OF 3 CAKE TINS PANTRY DESIGN
## 502 481
## REGENCY CAKESTAND 3 TIER JUMBO BAG RED RETROSPOT
## 457 414
## SET OF 6 SPICE TINS PANTRY DESIGN (Other)
## 351 93630
##
## element (itemset/transaction) length distribution:
## sizes
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## 411 135 139 120 140 87 101 115 116 98 118 86 84 92 86 113 84 79 103 74
## 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
## 76 73 61 56 33 42 47 46 53 44 35 28 29 36 26 30 17 21 31 19
## 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
## 29 24 18 22 15 17 13 23 20 15 13 16 16 12 11 8 9 11 5 12
## 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
## 7 3 8 9 8 5 7 6 9 7 8 4 6 5 5 4 2 7 3 1
## 81 82 83 84 85 86 87 88 89 90 92 93 95 96 97 98 101 104 106 107
## 2 4 1 1 3 2 1 3 6 3 1 3 2 2 1 4 3 3 3 2
## 108 109 110 111 113 114 116 117 118 119 120 122 124 126 127 129 130 131 135 138
## 1 2 1 3 1 1 1 1 1 1 1 1 1 1 2 1 2 1 1 2
## 139 140 141 143 144 147 149 151 153 154 155 156 157 158 159 162 165 166 168 169
## 1 1 1 1 3 2 3 2 2 1 1 1 1 1 1 1 2 2 2 2
## 171 172 174 175 177 178 180 182 185 186 189 192 193 198 199 204 206 208 214 215
## 1 1 1 1 3 2 2 2 1 1 1 1 1 1 1 2 1 2 1 1
## 216 219 222 223 224 225 228 230 235 250 271 280 285 288 298 332 333 339 345 348
## 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## 350 354 358 370 376 382 400 404 408 414 416 428 454 458 500
## 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1
##
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.00 5.00 15.00 25.37 29.00 500.00
##
## includes extended item information - examples:
## labels
## 1
## 2 4 PURPLE FLOCK DINNER CANDLES
## 3 OVAL WALL MIRROR DIAMANTE
##
## includes extended transaction information - examples:
## transactionID
## 1 539993
## 2 539997
## 3 539998En este resumen, podemos encontrar información interesante. Por ejemplo:
Contamos con 3777 transacciones (carritos de compra) y 2929 items.
La densidad es de 0.866%. Densidad muy baja si la comparamos con nuestro ejemplo del Capítulo 2. Pero este resultado es normal dada la gran cantidad de productos disponibles. En general, para este tipo de bases de datos de estos tamaños es común observar densidades de esta magnitud.
También podemos ver que los ítems más frecuentes en las canastas son: WHITE HANGING HEART T-LIGHT HOLDER, SET OF 3 CAKE TINS PANTRY DESIGN , REGENCY CAKESTAND 3 TIER, JUMBO BAG RED RETROSPOT, SET OF 6 SPICE TINS PANTRY DESIGN, (Other).
El paquete arule permite construir rápidamente visualizaciones como la matriz de ítems (item matrix) que se discutió en la Sección 2.2. La función image() solo necesita como único argumento un objeto con las transacciones (de clase transactions) para crear la matriz de ítems. Esta función tiene más argumentos que permiten personalizar el gráfico, como xlab y ylab para cambiarle los nombres a los ejes. El siguiente código genera la Figura 3.1:
Figura 3.1: Items por transacción (matriz de items)
La Figura 3.1 muestra lo que se intuía con el resultado de la densidad. Es una matriz poco poblada. Con este tipo de visualizaciones tenemos que tener mucho cuidado. Si mostramos demasiadas transacciones a la vez (por ejemplo, con millones de transacciones), esta visualización típicamente no informa mucho y puede tomar mucho tiempo y demandar muchos recursos de tu máquina e incluso bloquear tu computador. En este caso no parece agregar mucho valor esta visualización. ¡Siempre tenemos que intentarlo! No sabremos si una visualización funciona o no hasta no intentarlo y verla.
El paquete arules también incluye una función que permite visualizar los ítems (itemsets de un solo elemento) con mayor popularidad. La función itemFrequencyPlot() tiene como argumentos esenciales un objeto con las transacciones (de clase transactions) y el número de productos con la mayor frecuencia que se quieren visualizar (topN). Por ejemplo, hagamos un gráfico para el top 10 de ítems de mayor frecuencia. Esto se puede lograr con el siguiente código:
El resultado de evaluar esta línea de código no se presenta para ahorrar espacio.
Existen otros argumentos de la función que nos facilitan continuar personalizando la visualización. Por ejemplo, el argumento type nos permite que el gráfico de barras se presente con la frecuencia relativa34 (type = “relative”) o absoluta (type = “absolute”)35. También podemos hacer que las barras sean horizontales con el argumento horiz = TRUE. En la Figura 3.2 se presenta otra versión del gráfico que acabas de realizar. ¡Intenta replicar esta visualización!
Figura 3.2: Los 5 productos con mayor frecuencia en las transacciones
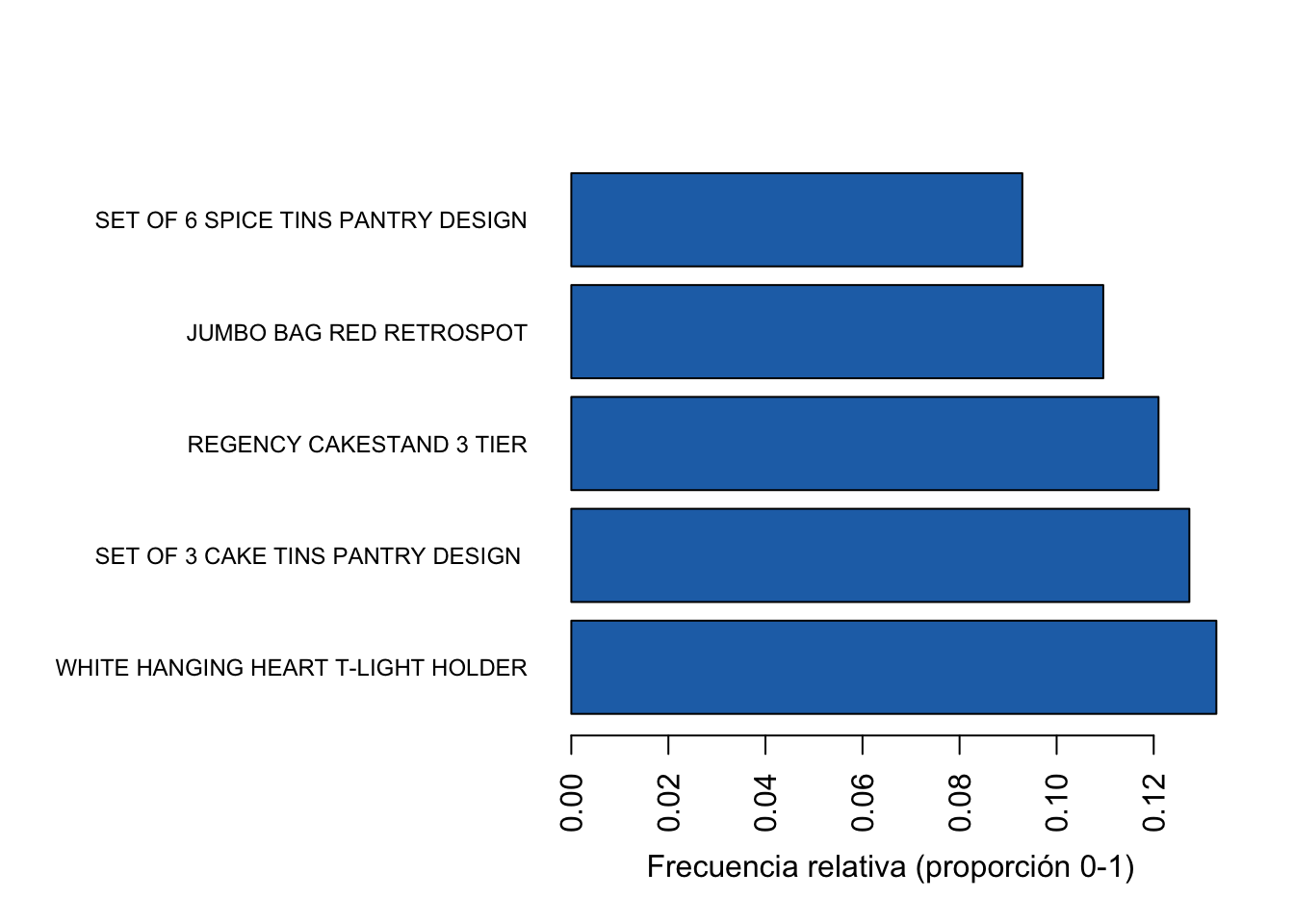
La Figura 3.2 muestra los mismos resultados que ya habíamos identificado en el resumen, pero de una manera más amigable. No obstante, las visualizaciones del paquete arules emplean la base de R. Ya sabemos que el paquete ggplot2 (Wickham, 2016) genera visualizaciones más flexibles36. Podemos construir rápidamente una función que emplee los paquetes ggplot2, tidyverse (Wickham et al., 2019) y arules para generar una visualización similar.
A continuación se presenta una función que crea un objeto de clase ggplot al que se le pueden adicionar capas como queramos. Esta función es una versión levemente modificada de lukeA (2017).
itemFrequencyGGPlot <- function(x, topN, color) {
require(tidyverse)
require(ggplot2)
require(arules)
x %>%
# Calcular las frecuencias
# relativas para cada ítem
itemFrequency %>%
# Organizar
sort %>%
# Extraer los items deseados
tail(topN) %>%
# Crear data.frame
as.data.frame %>%
tibble::rownames_to_column() %>%
# Generar la visualización
ggplot(aes(reorder(rowname, `.`),`.`)) +
geom_col(fill= color) +
coord_flip()
} En la Figura 3.3 se presenta una visualización creada con esta función. ¡Intenta replicarla!
Figura 3.3: Los 10 productos con mayor frecuencia en las transacciones (empleando ggplot2)
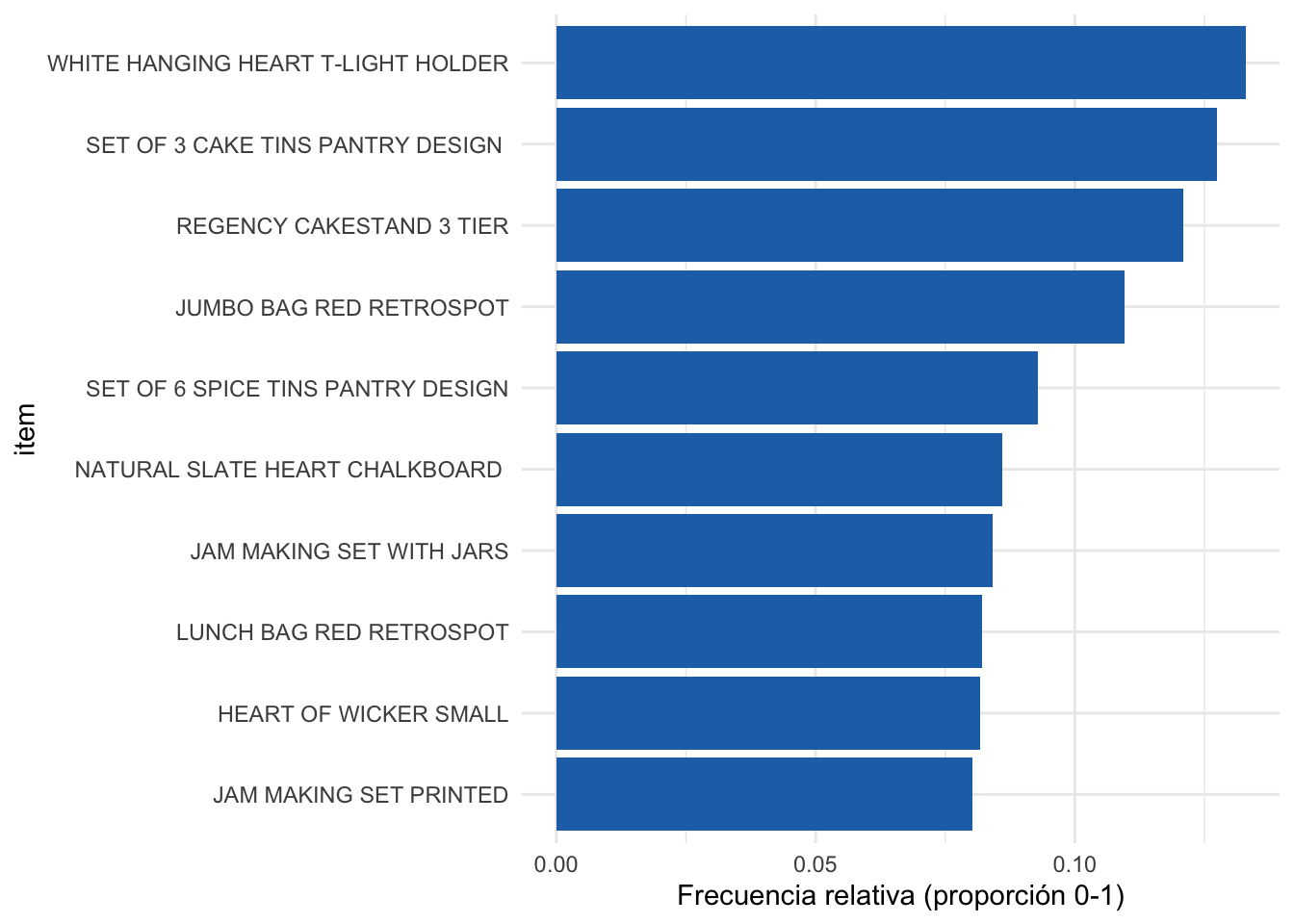
Continuando con la exploración de los datos, en algunas ocasiones podemos querer inspeccionar algunas canastas. Esto lo podemos hacer con la función inspect() del paquete arules. Con esta es posible inspeccionar un grupo de transacciones o una en específico. Por ejemplo, inspeccionemos las dos primeras canastas con la siguiente línea de código:
## items transactionID
## [1] {BLUE POLKADOT WRAP,
## CAST IRON HOOK GARDEN FORK,
## CHILDRENS APRON APPLES DESIGN,
## COFFEE MUG APPLES DESIGN,
## COFFEE MUG PEARS DESIGN,
## JAM MAKING SET PRINTED,
## JUMBO BAG PINK POLKADOT,
## JUMBO BAG RED RETROSPOT,
## LOVE HEART NAPKIN BOX ,
## PEG BAG APPLES DESIGN,
## RECIPE BOX RETROSPOT ,
## RECYCLING BAG RETROSPOT ,
## RED RETROSPOT CHILDRENS UMBRELLA,
## RED RETROSPOT SHOPPER BAG,
## RED RETROSPOT WRAP ,
## SET OF 6 T-LIGHTS EASTER CHICKS,
## WHITE HANGING HEART T-LIGHT HOLDER} 539993
## [2] {} 539997Veamos ahora las 3 últimas.
## items transactionID
## [1] {COFFEE SCENT PILLAR CANDLE,
## DAIRY MAID TOASTRACK,
## GROW A FLYTRAP OR SUNFLOWER IN TIN,
## ROSES REGENCY TEACUP AND SAUCER } 548547
## [2] {LOVE LARGE WOOD LETTERS ,
## REGENCY CAKESTAND 3 TIER} 548548
## [3] {CAKE PLATE LOVEBIRD WHITE,
## SWEETHEART CAKESTAND 3 TIER,
## ZINC FINISH 15CM PLANTER POTS} 548549Y veamos la canasta 102.
## items transactionID
## [1] {DOLLY HONEYCOMB GARLAND,
## GUMBALL COAT RACK,
## MINI FUNKY DESIGN TAPES,
## STRAWBERRY HONEYCOMB GARLAND ,
## TRADITIONAL WOODEN CATCH CUP GAME } 5402633.4 Construcción de las reglas
Como lo hemos discutido, el objetivo principal del MBA es encontrar reglas de asociación que permitan tomar decisiones. También discutimos en el Capítulo 2 cómo el algoritmo Apriori nos puede ayudar a encontrar relativamente rápido reglas que tengan sentido. A continuación implementaremos el algoritmo Apriori con el paquete arules empleando la función apriori().
Para calcular las reglas de asociación empleando el algoritmo Apriori, esta función solo necesita dos argumentos. Primero, los datos de la clase transactions. El segundo argumento corresponde a los parámetros para la búsqueda. Los parámetros permiten emplear una lista para establecer el umbral mínimo de soporte (supp), de confianza (conf) y el número mínimo de ítems en la regla (minlen). Para el caso del umbral del soporte, el valor por defecto es 0.1 (10%); para la confianza, el valor mínimo por defecto es 0.8 (80%). Recuerda que si no se especifican estos umbrales, se emplearán los valores por defecto. Finalmente, por defecto, el número mínimo de ítems en las reglas encontradas es 1 (minlen = 1). Esto implica que el algoritmo podrá encontrar reglas en las que el antecedente (a la izquierda LHS) sea un itemset vacío y el consecuente (resultado o a la mano derecha RHS) un elemento. Es decir, reglas como \(\left\{ \right\} \rightarrow \left\{ B \right\}\) o \(\emptyset \rightarrow \left\{ B \right\}\). Esta regla implica que se compraría \(B\) dado que aún la canasta está vacía. Normalmente, este tipo de reglas no son muy interesantes y, por tanto, es mejor emplear minlen = 2 para no permitir reglas con conjuntos vacíos en el antecedente.
Encontremos las reglas de asociación con el algoritmo Apriori para las transacciones de la empresa en línea con un soporte y confianza mínimos del 1%37 y 80%, respectivamente. Esto se puede hacer empleando el siguiente código:
# Aplicar el algoritmo Apriori
reglas <- apriori(datos_tra,
parameter = list(supp = 0.01, conf = 0.8,
minlen = 2))
# Chequear el tipo de objeto
class(reglas)
# Mostrar las reglas
reglasHemos encontrado 324 reglas que están almacenadas en el objeto reglas. Estas reglas no están guardadas en un orden en especial. Por eso es importante organizarlas antes de verlas, concentrémonos por ahora solo en las cinco primeras reglas. Organicemos las reglas por lift e inspecciones las cinco primeras reglas empleando el siguiente código:
## lhs rhs support confidence coverage lift count
## [1] {HERB MARKER MINT,
## HERB MARKER PARSLEY,
## HERB MARKER THYME} => {HERB MARKER CHIVES } 0.01006089 0.8636364 0.01164946 72.48788 38
## [2] {HERB MARKER MINT,
## HERB MARKER PARSLEY} => {HERB MARKER CHIVES } 0.01032566 0.8297872 0.01244374 69.64681 39
## [3] {HERB MARKER PARSLEY,
## HERB MARKER ROSEMARY,
## HERB MARKER THYME} => {HERB MARKER CHIVES } 0.01006089 0.8260870 0.01217898 69.33623 38
## [4] {HERB MARKER PARSLEY,
## HERB MARKER THYME} => {HERB MARKER CHIVES } 0.01032566 0.8125000 0.01270850 68.19583 39
## [5] {HERB MARKER PARSLEY,
## HERB MARKER ROSEMARY} => {HERB MARKER CHIVES } 0.01006089 0.8085106 0.01244374 67.86099 38De manera similar, inspeccionemos las cinco reglas con la mayor confianza empleando la siguiente línea de código:
# inspeccionar las 5 primeras reglas con mayor confianza
inspect(head(sort(reglas, by="confidence"), 5))## lhs rhs support confidence coverage lift count
## [1] {CHRISTMAS TREE DECORATION WITH BELL} => {DOTCOM POSTAGE} 0.01006089 1 0.01006089 20.30645 38
## [2] {HERB MARKER BASIL,
## HERB MARKER CHIVES } => {HERB MARKER THYME} 0.01006089 1 0.01006089 65.12069 38
## [3] {HERB MARKER CHIVES ,
## HERB MARKER ROSEMARY} => {HERB MARKER THYME} 0.01085518 1 0.01085518 65.12069 41
## [4] {CAKE STAND VICTORIAN FILIGREE MED,
## VINTAGE PAISLEY STATIONERY SET} => {DOTCOM POSTAGE} 0.01006089 1 0.01006089 20.30645 38
## [5] {BEADED CRYSTAL HEART PINK ON STICK,
## HEART DECORATION RUSTIC HANGING } => {DOTCOM POSTAGE} 0.01059042 1 0.01059042 20.30645 40Y finalmente, miremos las cinco reglas con el mayor soporte empleando el siguiente código:
## lhs rhs support confidence coverage lift count
## [1] {PINK REGENCY TEACUP AND SAUCER,
## ROSES REGENCY TEACUP AND SAUCER } => {GREEN REGENCY TEACUP AND SAUCER} 0.02832936 0.9553571 0.02965316 15.097841 107
## [2] {GREEN REGENCY TEACUP AND SAUCER,
## PINK REGENCY TEACUP AND SAUCER} => {ROSES REGENCY TEACUP AND SAUCER } 0.02832936 0.8770492 0.03230077 14.096233 107
## [3] {REGENCY CAKESTAND 3 TIER,
## ROSES REGENCY TEACUP AND SAUCER } => {GREEN REGENCY TEACUP AND SAUCER} 0.02382844 0.8333333 0.02859412 13.169456 90
## [4] {SET/6 RED SPOTTY PAPER CUPS} => {SET/6 RED SPOTTY PAPER PLATES} 0.02329891 0.8461538 0.02753508 24.968149 88
## [5] {JUMBO BAG BAROQUE BLACK WHITE,
## JUMBO STORAGE BAG SUKI} => {JUMBO BAG RED RETROSPOT} 0.02091607 0.8144330 0.02568176 7.430226 79Nota que, dependiendo del criterio que empleemos, las reglas más importantes son diferentes.
3.5 Trabajando con las reglas
Hasta el momento hemos encontrado 324 reglas. Estas son muchas reglas para analizar, esto es común cuando se hace un MBA. Como lo discutimos en la Sección 2.6, algunas reglas pueden ser redundantes, en el sentido de que no aportan conocimientos adicionales. Recordemos que una regla es redundante si existe otra regla más general con una confianza igual o mayor. Una regla más general es aquella que tiene el mismo itemset como consecuente (RHS), pero uno o más elementos menos en el antecedente (LHS) (Ver Sección 2.6).
Así, una de las primeras tareas que tenemos que hacer con las reglas encontradas es descartar aquellas que sean redundantes. Las reglas redundantes se pueden encontrar con la función is.redundant() del paquete arules. Para nuestro ejemplo, las reglas redundantes las podemos encontrar de la siguiente manera:
# Encontrar reglas redundantes
reglas_redundantes <- is.redundant(reglas)
# Chequear clase del objeto
class(reglas_redundantes)## [1] "logical"## [1] 30Tenemos 30 reglas redundantes. Podemos descartar esas reglas redundantes y quedarnos con aquellas que sí son pertinentes de la siguiente manera:
# Filtrar las reglas redundantes y
# mantener solo las no redundantes
reglas <- reglas[!reglas_redundantes]Ahora contamos con 294 reglas (no redundantes). Si queremos, podemos transformar las reglas a un objeto de clase data.frame con el siguiente código:
# Transformar reglas a clase data.frame
reglas_df = as(reglas, "data.frame")
# visualizar las reglas no redundantes
glimpse(reglas_df)## Rows: 294
## Columns: 6
## $ rules <chr> "{HERB MARKER CHIVES } => {HERB MARKER BASIL}", "{HERB MARK…
## $ support <dbl> 0.01006089, 0.01059042, 0.01085518, 0.01138470, 0.01111994,…
## $ confidence <dbl> 0.8444444, 0.8888889, 0.9111111, 0.9555556, 0.9333333, 0.88…
## $ coverage <dbl> 0.01191422, 0.01191422, 0.01191422, 0.01191422, 0.01191422,…
## $ lift <dbl> 61.33590, 63.34591, 60.37310, 62.22644, 60.77931, 58.90058,…
## $ count <int> 38, 40, 41, 43, 42, 40, 38, 42, 43, 43, 47, 47, 48, 48, 47,…Esto permitiría manipular las reglas como estamos acostumbrados. Por ejemplo, podrías emplear los paquetes dplyr (Wickham et al., 2021) o ggplot2 para seguir analizando las reglas.
3.5.1 Jugando con los parámetros del algoritmo Apriori (avanzado)
Seleccionar el umbral mínimo para el soporte y la confianza afecta sustancialmente el número de reglas con las que finalmente terminamos. Escoger estos umbrales (parámetros) para el algoritmo no es una tarea sencilla. La elección de los umbrales de soporte y confianza es un verdadero problema práctico al emplear los algoritmos de minería de reglas de asociación. Por ejemplo, buscar reglas de asociación empleando un umbral de soporte alto elimina las reglas con ítems inusuales sin tener en cuenta el valor de confianza de estas reglas. Por otra parte, cuando el umbral de soporte es bajo, se genera un elevado número de reglas y, en consecuencia, al usuario final le resulta muy difícil, si no imposible, utilizarlas. En otras palabras, es importante jugar un poco con estos parámetros hasta encontrar el resultado adecuado para cada juego de datos.
En algunos casos nos podemos ayudar un poco de la fuerza “bruta” de los computadores para entender el efecto final sobre el número de reglas de asociación de nuestra elección de dichos umbrales.
Calculemos el número de reglas de asociación que encontrará el algoritmo Apriori con un soporte de 0.01. Para esto podemos emplear loops38 de la siguiente manera (asegúrate que puedes seguir el código):
# Fijar los niveles para la confianza
confidenceLevels <- seq(from=0.95, to=0.5, by=-0.05)
# Vector vacío para guardar los resultados
r_res_01 <- NULL
# Loops para Algoritmo Apriori con soporte del 0.01
for (i in 1:length(confidenceLevels)) {
r_res_01[i] <-
length(apriori(datos_tra,
parameter=list(sup=0.01,
conf=confidenceLevels[i]),
control = list(verbose=F)))
}Ahora grafiquemos estos resultados. El siguiente código genera la Figura 3.4:
# Construir el data.frame con datos a visualizar
data_loops <- as.data.frame(confidenceLevels, r_res_01)
# Visualizar los resultados
ggplot( data_loops, aes(x = confidenceLevels, y=r_res_01)) +
geom_point() +
geom_line() +
xlab("Confianza") +
ylab("Número de reglas encontradas") +
theme_minimal() Figura 3.4: Número de reglas encontradas por el algoritmo Apriori para diferentes valores de confianza manteniendo el soporte en 0.01
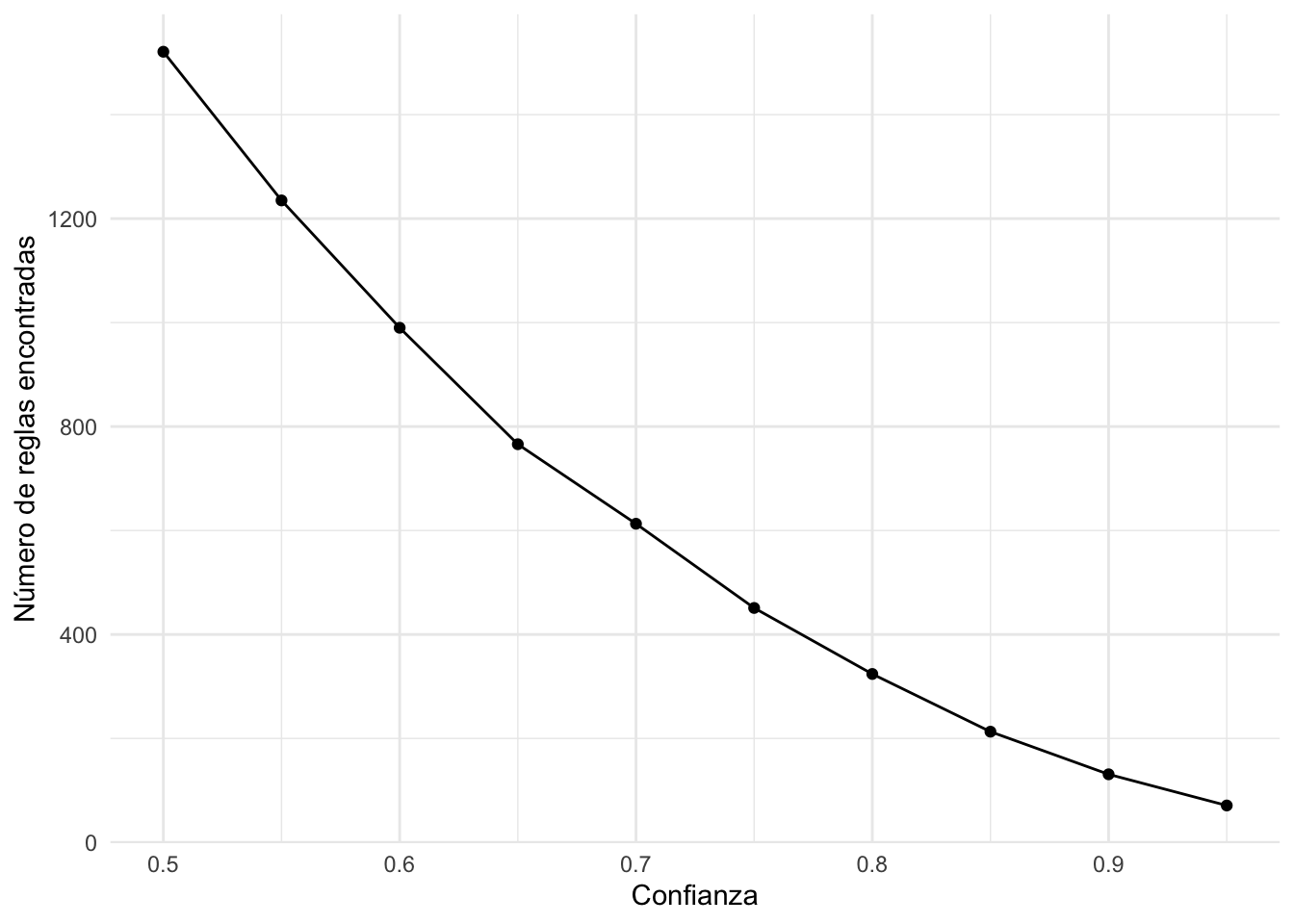
Podemos ver cómo se afecta nuestro número de reglas cuando el soporte aumenta. Y comparemos este resultado con un soporte más alto (0.02).
# Vector vacío para guardar los resultados
r_res_02 <- NULL
# Loops para Algoritmo Apriori con soporte del 0.01
for (i in 1:length(confidenceLevels)) {
r_res_02[i] <-
length(apriori(datos_tra,
parameter=list(sup=0.02,
conf=confidenceLevels[i]),
control = list(verbose=F)))
}
# Unir los resultados
nb_rules = data.frame(r_res_01, r_res_02,
confidenceLevels)Y finalmente, visualicemos estos resultados (Ver Figura 3.5).
Figura 3.5: Número de reglas encontradas por el algoritmo Apriori para diferentes valores de confianza con soportes de 0.01 y 0.02
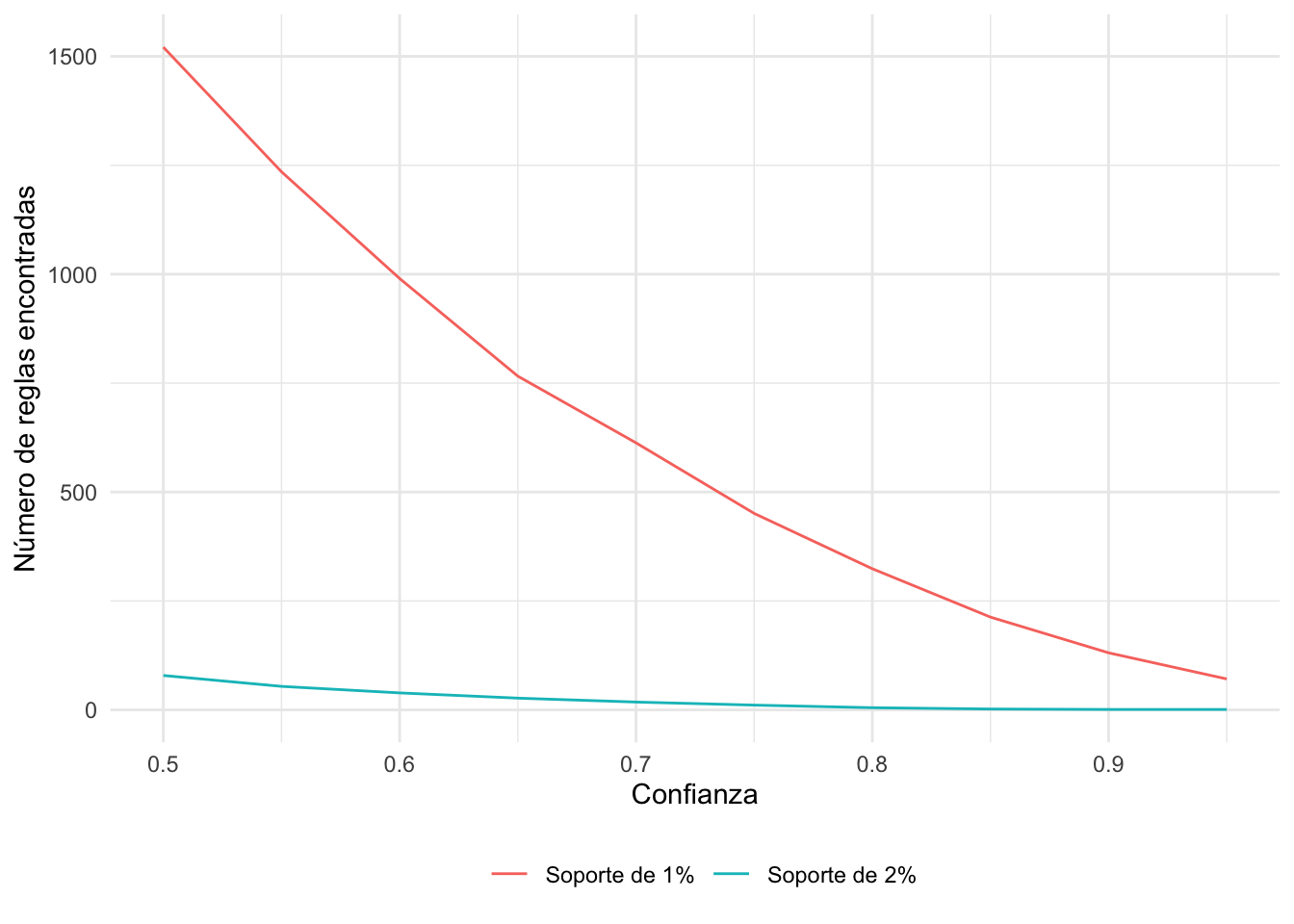
Esto justifica por qué nuestro soporte fue tan bajo para este caso.
3.5.2 Trabajando con reglas para productos específicos
En algunas ocasiones el tomador de decisiones estará interesado en un producto en específico. Por ejemplo, se desea emplear las reglas de asociación para promover la venta de un producto. En este caso, nuestro producto deberá estar en el consecuente (LHS) de la regla. O podemos querer buscar un producto que pueda ser impulsado en forma de combo con el producto estrella. En ese caso nos interesará buscar reglas con el producto estrella como antecedente (RHS) de la regla.
Así, es frecuente que en la práctica queramos buscar itemsets específicos o reglas específicas dentro del conjunto de todas las reglas no redundantes extraídas. Esto se puede hacer de manera sencilla en R. La función apriori() tiene otro argumento que aún no hemos usado, que es appearance (una traducción en este contexto sería aparición). Con este argumento podemos encontrar aquellas reglas que tengan como LHS o RHS los itemsets deseados.
Supongamos por un momento que queremos encontrar las reglas de asociación que permitan impulsar la compra del producto “HERB MARKER THYME”39. Es decir, reglas que tengan al producto “HERB MARKER THYME” a la derecha de la regla (RHS). Esto lo podemos hacer empleando el argumento appearance, agregando como lista el requerimiento que deseamos; en este caso rhs = “HERB MARKER THYME”. Es decir, el código sería el siguiente:
# Aplicar el algoritmo Apriori para encontrar reglas
# con "HERB MARKER THYME" en el rhs
regla_thyme_rhs <-
apriori(datos_tra,
parameter = list(supp=0.01, conf=0.8, minlen=2),
appearance = list(rhs = "HERB MARKER THYME"),
control = list(verbose=F))
regla_thyme_rhs## set of 22 rulesNota que además incluimos el argumento control = list(verbose=F). Esto evita que se impriman los resultados en la consola de mensajes mientras se realiza el cálculo. Encontramos 22 reglas con este ítem en el consecuente. Igual que antes, podemos descartar las reglas redundantes y visualizar los resultados ordenando por alguna de las métricas de interés.
# Encontrar reglas redundantes
regla_thyme_rhs_red <- is.redundant(regla_thyme_rhs)
# Contar el número de reglas redundantes
sum(regla_thyme_rhs_red)## [1] 8# Crear objeto con reglas no redundantes
regla_thyme_rhs = regla_thyme_rhs[!regla_thyme_rhs_red]
# Ver el objeto con las reglas no redundantes
regla_thyme_rhs## set of 14 rulesAhora miremos las cinco reglas con la mayor confianza. Para esto podemos emplear el siguiente código:
# Inspeccionar las top 5 reglas por confianza
inspect(head(sort(regla_thyme_rhs, by="confidence"), 5))## lhs rhs support confidence coverage lift count
## [1] {HERB MARKER BASIL,
## HERB MARKER CHIVES } => {HERB MARKER THYME} 0.01006089 1.0000000 0.01006089 65.12069 38
## [2] {HERB MARKER CHIVES ,
## HERB MARKER ROSEMARY} => {HERB MARKER THYME} 0.01085518 1.0000000 0.01085518 65.12069 41
## [3] {HERB MARKER PARSLEY,
## HERB MARKER ROSEMARY} => {HERB MARKER THYME} 0.01217898 0.9787234 0.01244374 63.73514 46
## [4] {HERB MARKER CHIVES ,
## HERB MARKER MINT} => {HERB MARKER THYME} 0.01085518 0.9761905 0.01111994 63.57020 41
## [5] {HERB MARKER CHIVES ,
## HERB MARKER PARSLEY} => {HERB MARKER THYME} 0.01032566 0.9750000 0.01059042 63.49267 39¿Qué puedes concluir? ¿Qué acción de mercadeo puedes sugerir?
Ahora miremos reglas que tengan como antecedente (LHS) el ítem “HERB MARKER ROSEMARY”. De manera análoga, podemos emplear el siguiente código:
regla_rosemary_lhs <-
apriori(datos_tra,
parameter = list(supp=0.01, conf=0.8, minlen=2),
appearance = list(lhs = "HERB MARKER ROSEMARY"),
control = list(verbose=F))
# Encontrar reglas redundantes
regla_rosemary_lhs_red <- is.redundant(regla_rosemary_lhs)
# Contar el número de reglas redundantes
sum(regla_rosemary_lhs_red)## [1] 0# no hay reglas redundantes
# Inspeccionar las top 5 reglas por confianza
inspect(sort(regla_rosemary_lhs, by="confidence"))## lhs rhs support confidence
## [1] {HERB MARKER ROSEMARY} => {HERB MARKER THYME} 0.01456182 0.9649123
## [2] {HERB MARKER ROSEMARY} => {HERB MARKER MINT} 0.01350278 0.8947368
## [3] {HERB MARKER ROSEMARY} => {HERB MARKER BASIL} 0.01244374 0.8245614
## [4] {HERB MARKER ROSEMARY} => {HERB MARKER PARSLEY} 0.01244374 0.8245614
## coverage lift count
## [1] 0.01509134 62.83575 55
## [2] 0.01509134 58.26588 51
## [3] 0.01509134 59.89170 47
## [4] 0.01509134 58.76167 47En este resultado se ha definido la etiqueta (herb marker) para romero (Rosemery) como el antecedente de la regla de asociación. Por lo tanto, el consecuente nos indica los productos que los consumidores compran dado que ya tienen en sus carritos de compra la etiqueta para romero. En este caso, las cuatro reglas encontradas tienen un lift muy grande (superior a 1) y una confianza mayor a 82.5%. Es decir, se trata de reglas con una alta probabilidad de ocurrencia. Los productos que se encuentran como consecuente, cuando el antecedente es la etiqueta para romero, son las etiquetas para el tomillo (thyme), la menta (mint), la albahaca (basil) y el perejil (parsley).
El soporte de cada una de estas reglas (frecuencia con la que un consumidor compra la cesta que contiene la etiqueta para el romero y las otras etiquetas de hierbas) es de aproximadamente el 1%. Adicionalmente, una vez el consumidor incluye la etiqueta para romero en su canasta de compras, hay una confianza del 96% de que también incluya la etiqueta para tomillo, del 82% de que incluya la etiqueta para la menta y del 82% de que incluya la etiqueta para el perejil.
Teniendo en cuenta el resultado del lift (la popularidad conjunta de ambos ítems), vemos que hay una asociación positiva (lift > 1) entre la compra de la etiqueta para romero y la compra de cada una de las otras etiquetas de hierbas (tomillo, menta, albahaca o perejil). La cobertura (coverage) nos indica que la regla etiqueta de romero-tomillo (o una de las otras etiquetas para hierbas) se aplica con una probabilidad del 1.5%.
La pregunta que te puedes estar haciendo en estos momentos es: ¿por qué quisiera el tomador de decisiones observar las reglas de asociación con el antecedente de etiquetas para romero? Al encontrar estas reglas (reglas con el ítem “HERB MARKER ROSEMARY” en el LHS), por ejemplo, sería posible observar cuáles productos podrían ofrecerse de manera conjunta con la etiqueta de romero para generar valor al consumidor.
El combo es relevante para el consumidor porque le ofrece un producto complementario de su interés; adicionalmente, obtiene ambos productos a un menor precio en comparación con la compra individual.
3.6 Comentarios finales
En este Capítulo hemos estudiado paso a paso cómo realizar un MBA en R. Empleando una base relativamente grande con datos transaccionales, pudimos encontrar reglas de asociación no redundantes. Estas reglas de asociación son el insumo para la toma de decisiones en el negocio. De esta manera, tanto el científico de datos como el analytics translator deben conocer y establecer conjuntamente las reglas de asociación con las que se alimenta el MBA; este es el resultado que guiará las decisiones estratégicas. Aunque el científico de datos se encarga del detalle técnico en R, es importante que el analytics translator comprenda el proceso de creación de reglas para entender las implicaciones de las reglas establecidas. De estas reglas depende el resultado y los insights que conllevan a la toma de decisión.
Una vez que contamos con las reglas de asociación, las preguntas de negocio empezarán a fluir y la tarea del científico de datos termina e inicia la del analytics translator para acompañar en el uso de dichas reglas para la toma de decisiones. En el Capítulo 4 estudiaremos cómo visualizar los resultados para facilitar este proceso de toma de decisiones.
Antes de terminar este Capítulo, guarda el espacio de trabajo (workspace), lo emplearemos en el Capítulo 4. Eso lo puedes hacer con el siguiente código:
Referencias
¡Intenta calcular \(2^{2981}\) en R! Ese es el número máximo de itemsets posibles.↩︎
¡Intenta calcular \(3^{2981} - 2^{2981+1} + 1\) en R! Ese es el número máximo de reglas posibles.↩︎
Para una descripción de esta clase puedes consultar Alonso & Ocampo (2022).↩︎
También podríamos emplear el SKU, pero de pronto los números de los SKU no nos dirán mucho. Por eso emplearemos mejor la descripción.↩︎
Es decir, como proporción.↩︎
Es decir, como el número de veces observado.↩︎
Si deseas recordar cómo funciona el paquete ggplot2 puedes consultar Alonso & Largo (2023).↩︎
Este soporte parece muy pequeño, pero recuerda que los cuatro ítems con la mayor frecuencia relativa están muy cerca a 0.1. Si empleamos un soporte igual a 0.10, terminamos sin reglas (ver Figura 3.3). ¡Inténtalo! Por eso, empleamos un soporte relativamente bajo. Al final de la Sección 3.5.1 se discutirá más en detalle esta elección del soporte.↩︎
Para una introducción a los loops, puedes consultar Alonso (2021).↩︎
Un “HERB MARKER” (marcador de hierbas) es una pequeña estaca o etiqueta, usualmente de madera, plástico o cerámica resistente a la intemperie, que se clava en la matera o la huerta para identificar la especie aromática sembrada. Facilita el cuidado del cultivo y la correcta recolección de cada hierba.↩︎