4 Visualización de resultados y reglas
4.1 Introducción
En los primeros dos capítulos de este libro se define el concepto de MBA (sigla del término en inglés Market Basket Analysis o análisis de canasta) junto con un ejemplo que facilita la apropiación del concepto. En el Capítulo 3 estudiamos cómo aplicar los conceptos empleando R para encontrar reglas de asociación que cumplieran unos criterios mínimos de soporte y confianza empleando el algoritmo Apriori. Adicionalmente, vimos cómo extraer reglas de asociación para productos específicos, ya fueran como antecedentes en la regla (LHS) o consecuente (RHS).
En este Capítulo nos concentraremos en cómo visualizar los resultados y cómo brindar herramientas interactivas a los tomadores de decisiones a partir de las reglas que aprendimos a encontrar en el Capítulo 3. La tarea de visualizar los resultados del MBA es una tarea compartida entre científico de datos y analytics translator. El analytics translator garantizará que las visualizaciones producidas por los científicos de datos sean de fácil comprensión para los tomadores de decisiones de la organización.
En el trabajo del científico de datos y del analytics translator, es importante, después de encontrar las reglas de asociación, construir visualizaciones que transmitan confianza en el análisis realizado y que también permitan usar los resultados para tomar decisiones. En ese orden de ideas, este Capítulo estará centrado en dos tipos de visualizaciones: aquellas que comunican las métricas de las reglas de asociación (Ver Sección 4.2) y aquellas que permiten ver las reglas de asociación e interactuar con ellas (Ver Sección 4.3).
Este Capítulo explica al científico de datos los pasos para generar las visualizaciones y al analytics translator le permitirá conocer el tipo de visualizaciones que se emplean en este contexto y cómo se interpretan. El analytics translator puede omitir de este Capítulo el detalle del código en R. Lo que sí será importante para este rol es tener claras las herramientas disponibles para comunicar los resultados y su interpretación. Además, siempre es importante tener en cuenta que la construcción de visualizaciones es un trabajo conjunto entre el científico de datos y el analytics translator para asegurarse de que los insights son comunicados adecuadamente a los tomadores de decisiones.
En este Capítulo continuaremos con el ejemplo del capítulo anterior; carguemos el espacio de trabajo (workspace) que creamos al final del Capítulo 3. Esto lo puedes hacer con el siguiente código:
Recordemos que tenemos en el espacio de trabajo (workspace) por lo menos los siguientes objetos:
datos_tra: objeto de clase transactions con los datos de todas las transacciones de una empresa de comercio electrónico con sede en el Reino Unido para el primer trimestre de un año reciente.Datos_original: objeto de clase data.frame que contiene todas las variables originales.reglas: reglas de asociación detectadas con el algoritmo Apriori (umbral para el soporte de 0.01 y para la confianza de 0.8).regla_thyme_rhs: reglas de asociación detectadas con el algoritmo Apriori (umbral para el soporte de 0.01 y para la confianza de 0.8) con el ítem “HERB MARKER THYME” como consecuente (RHS).regla_rosemary_lhs: reglas de asociación detectadas con el algoritmo Apriori (umbral para el soporte de 0.01 y para la confianza de 0.8) con el ítem “HERB MARKER ROSEMARY” como antecedente (LHS).
En todos los casos, las reglas de asociación redundantes fueron descartadas. A continuación, estudiaremos algunas de las opciones disponibles para visualizar las métricas de los itemsets y de las reglas de asociación, así como las reglas de asociación como tal.
4.2 Visualizando las métricas de las reglas de asociación
Una vez que se ha empleado el algoritmo Apriori para elegir reglas de asociación, es común que se quiera visualizar las métricas de las reglas seleccionadas. Un gráfico común es un gráfico de dispersión con el soporte y la confianza. El paquete arulesViz (Hahsler, 2017) provee varias opciones para visualizar las métricas de las reglas y las reglas como tal. Este paquete incluye la función plot() para objetos de clase rules40. Esta función por defecto presenta una visualización del soporte (eje horizontal), la confianza (eje vertical) y el lift (el color). Por ejemplo, la Figura 4.1 permite visualizar estas tres métricas de cada una de las 294 reglas no redundantes encontradas en nuestro ejemplo.
Figura 4.1: Soporte, confianza y lift de todas las reglas no redundantes encontradas por el algoritmo Apriori
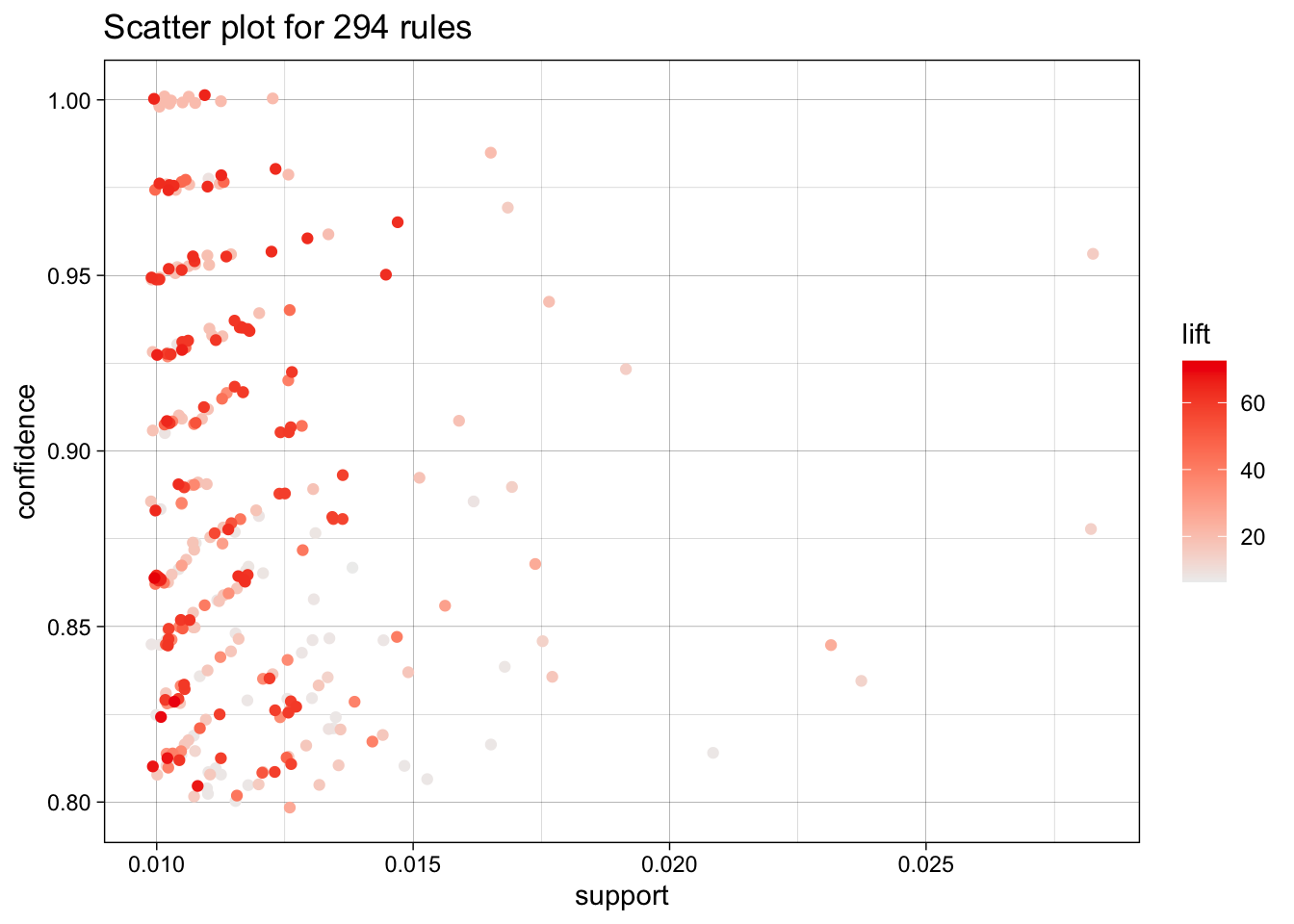
En la Figura 4.1 podemos ver tres insights importantes para la toma de decisiones. Primero, el soporte de la mayoría de las 294 reglas se concentra alrededor del 1%. Las reglas que descubre el algoritmo Apriori aparecen en muy pocas tirillas de compra (carritos de compra o tickets). Esto indica nichos específicos de comportamiento, con poco volumen, pero muy definidos, que podrían ser explotados con tácticas “one-to-one” (recomendaciones personalizadas, ofertas en la app, displays en punto de venta dirigidos a microsegmentos). Segundo, la confianza es sistemáticamente alta (entre 0.8 y 1.0) y el color rojo intenso señala lifts superiores a 30, incluso por encima de 60. En otras palabras, cuando el antecedente está presente, el consecuente casi siempre se añade al carrito y la probabilidad conjunta supera decenas de veces la esperada por azar. Esto valida la posibilidad de crear combos (bundles) o descuentos cruzados. Activar el producto “gatillo” garantiza con una alta probabilidad la venta del complementario (consecuente). Tercero, existen pocas reglas con soportes cercanos a la zona entre el 2.0% y el 2.5% y confianza mayor 0.85. Si bien el lift es algo menor, cubren una base de clientes mayor y, por tanto, son candidatos idóneos para campañas masivas (promociones en góndola, emailing general). Así, el gráfico sugiere un portafolio de reglas dual; por un lado, reglas de alto lift-bajo soporte para acciones hipersegmentadas que impulsen ticket promedio y fidelización, y por el otro lado, reglas de soporte medio-alto para iniciativas de category management que muevan volumen sin sacrificar la rentabilidad.
El código que generó Figura 4.1 es el siguiente:
La función plot() del paquete arulesViz permite cambiar las métricas que se presentan en los dos ejes empleando el argumento measure. Con el argumento shading podemos cambiar la métrica que le da color a los puntos. Por ejemplo, la Figura 4.2 se construye con el siguiente código:
# Visualizar las métricas de las reglas
plot(reglas,
measure = c("confidence", "lift"),
shading = "support")Figura 4.2: Soporte, confianza y lift de todas las reglas no redundantes encontradas por el algoritmo Apriori (Versión 2)
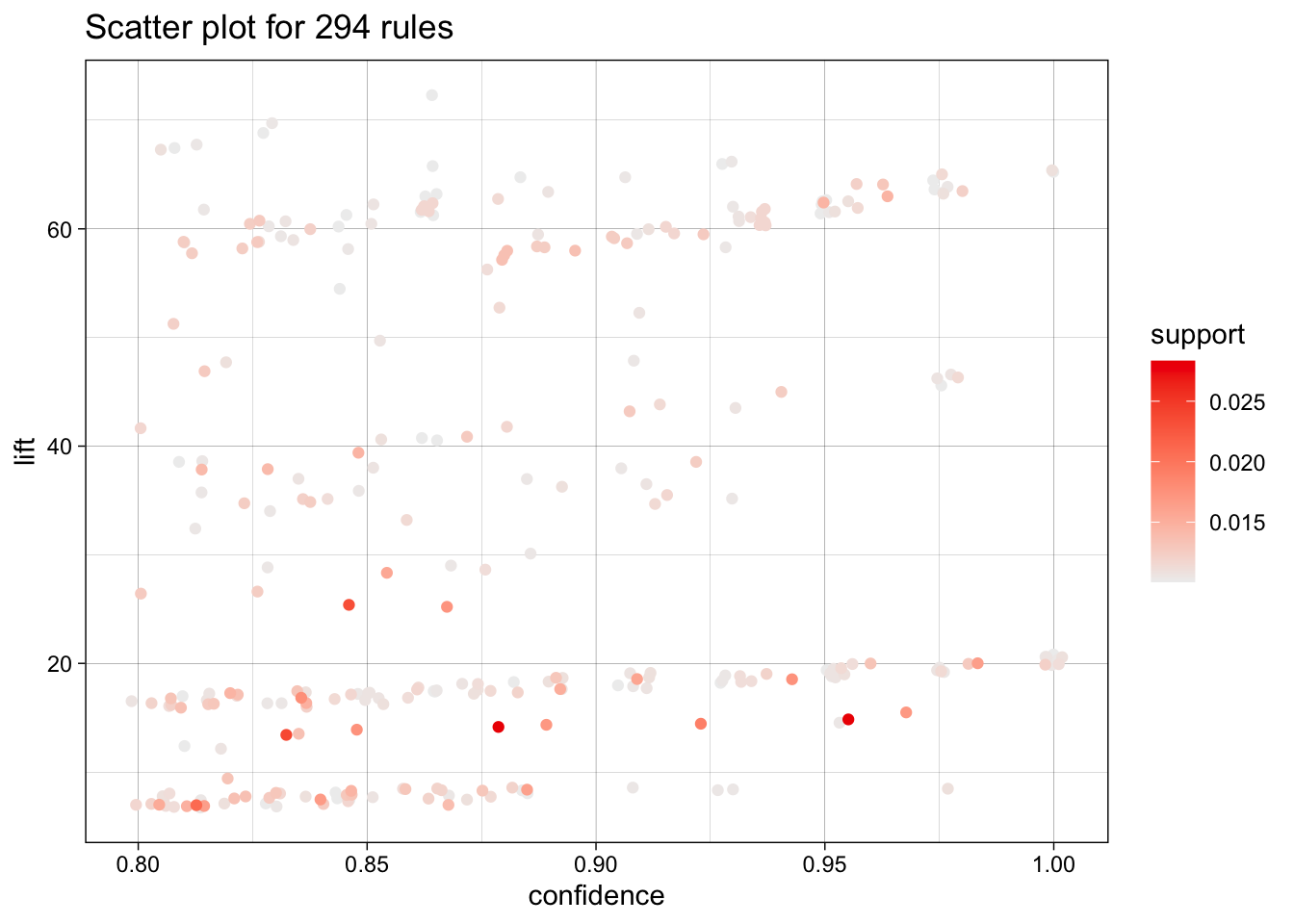
En la Figura 4.2 invertimos la perspectiva: el lift pasa al eje vertical y el soporte se codifica con la intensidad del color. Esta visualización alternativa refuerza los hallazgos ya descritos para la Figura 4.1. Los puntos más oscuros, reglas con mayor soporte, se agrupan en bandas de lift moderado (entre 15 y 25) y confianza alta (mayor a 0.85), confirmando su potencial para campañas masivas de category management. A la vez, se distinguen nubes más claras en la zona superior del gráfico (lift mayor a 50 y soporte menor al 1%), evidencia de oportunidades hipersegmentadas donde, aun con poco volumen, la probabilidad de compra conjunta se multiplica. Exactamente el tipo de reglas que habíamos recomendado para tácticas “one-to-one”. Así, ambas visualizaciones permiten comunicar un mismo mensaje estratégico: gestionar el portafolio de reglas según la combinación soporte-confianza-lift para equilibrar volumen y rentabilidad.
Adicionalmente, tenemos la opción de visualizar las métricas de manera diferente con el argumento method. Por defecto, la función plot() crea un gráfico de dispersión (method = “scatterplot”). Con este argumento podemos crear gráficos en forma de matriz (method = “matrix”) o en tres dimensiones41 method = “matrix3D”. En las Figuras 4.3 y 4.4 se reportan las métricas de todas las reglas empleando dos diferentes visualizaciones. ¡Intenta reproducir esas figuras!
Figura 4.3: Soporte, confianza y lift de todas las reglas no redundantes encontradas por el algoritmo Apriori (Versión matriz)
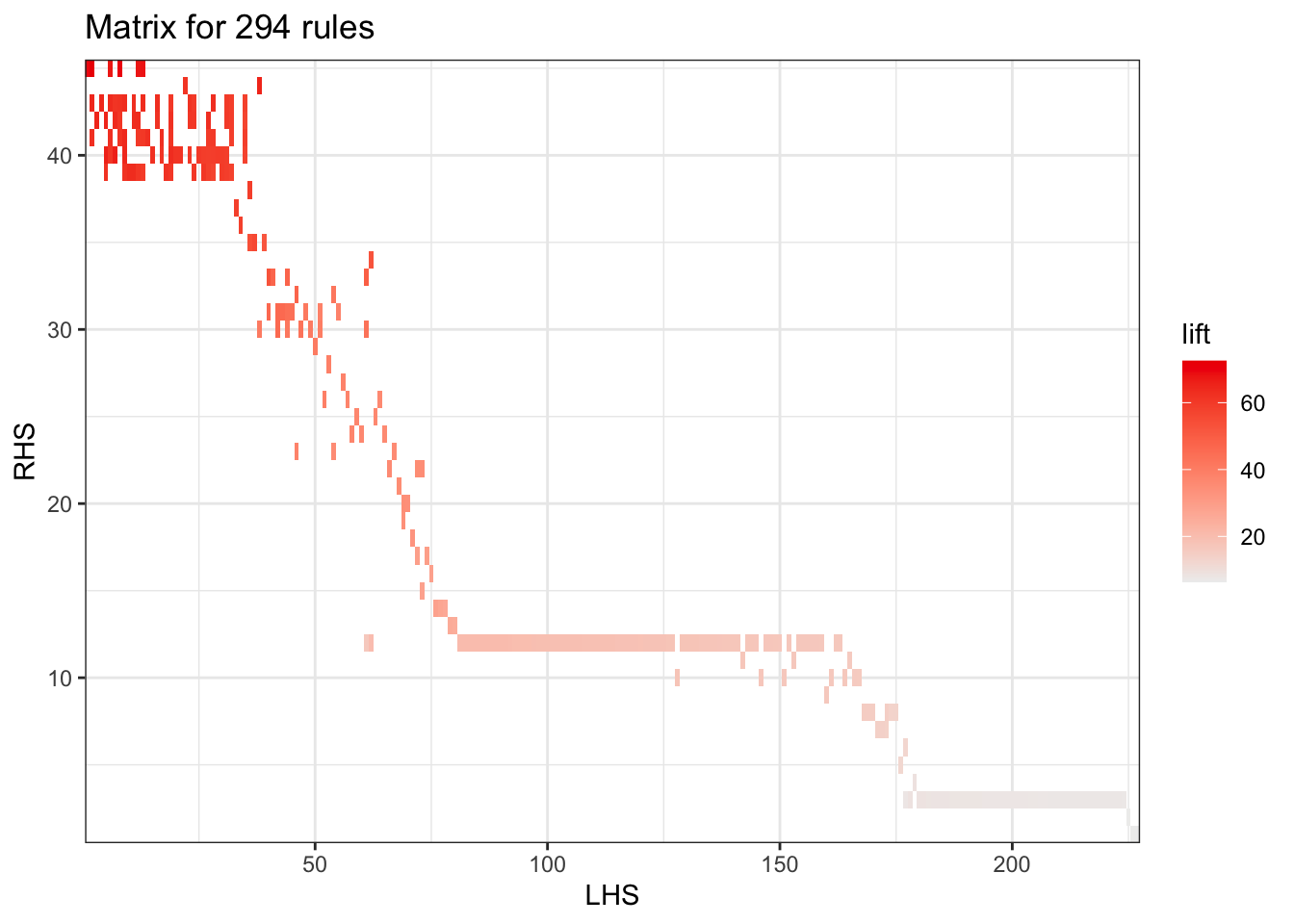
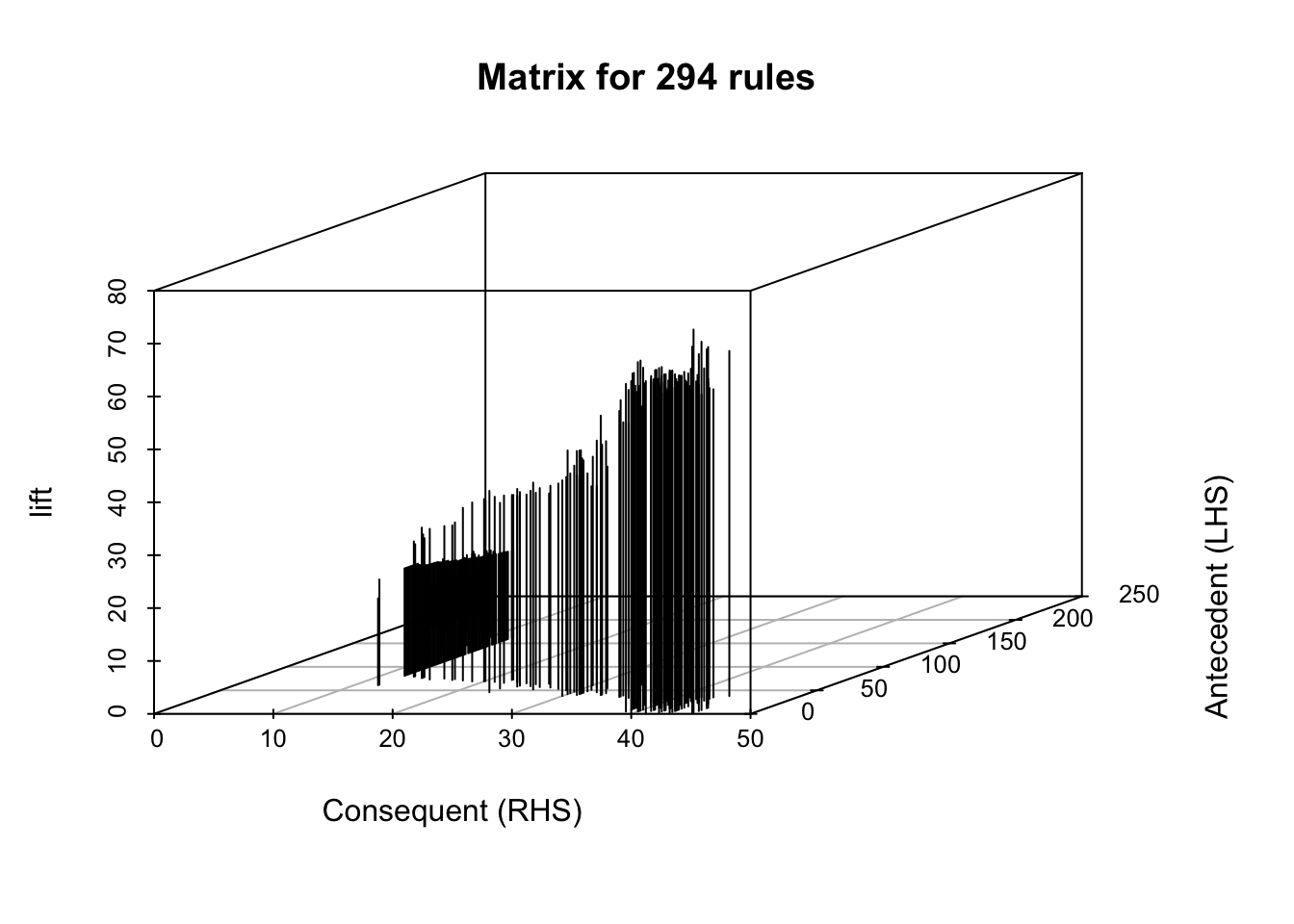
Figura 4.4: Soporte, confianza y lift de todas las reglas no redundantes encontradas por el algoritmo Apriori (Versión 3D)
En la Figura 4.3, obtenida con method = “matrix”, cada celda ubica una regla según el índice de su antecedente (eje LHS) y de su consecuente (eje RHS). El tono rojizo representa el lift. Dos patrones sobresalen. Primero, un bloque densamente rojo en la esquina superior izquierda, señal de que un grupo de productos actúa repetidamente como “gatillo” y “complemento” con lift superior a 40. Y segundo, un gradiente que se reduce en diagonal a medida que los índices aumentan, mostrando que las combinaciones menos comunes mantienen un lift importante, aunque menor, a medida que aumenta la variedad de ítems involucrados. Esta distribución confirma que la mayor tracción comercial se concentra en un subconjunto limitado de artículos clave, ideales para definir tácticas de cross-selling prioritarias.
La Figura 4.4 se crea con method = “matrix3D” y proyecta esas mismas reglas en un espacio tridimensional (LHS, RHS, lift). Aunque más difícil de leer, de ahí nuestra nota de cautela, la “selva” de barras verticales permite apreciar la dispersión del lift. La mayoría de las reglas se elevan entre 10 y 60, con unos cuantos picos que superan 70. La visualización corrobora la heterogeneidad ya detectada; pocas combinaciones generan lifts extraordinarios, mientras la mayoría sostiene valores sólidos que, sin llegar a ser excepcionales, respaldan estrategias de empaquetamiento estándar.
Juntas, las Figuras 4.3 y 4.4 complementan la historia narrada por las Figuras 4.1 y 4.2: un pequeño núcleo de productos concentra asociaciones fuertes y repetitivas (alto soporte y alto lift), alrededor del cual gravita un espectro de reglas de menor volumen pero todavía rentables.
En estos casos en los que existen tantas reglas, y que el usuario quisiera conocer las métricas de cada una de las reglas, puede ser una buena idea emplear una visualización interactiva. Las visualizaciones interactivas permiten a los usuarios realizar la exploración de datos para diferentes asociaciones. Es decir, es posible visualizar resultados para asociaciones específicas y así tomar decisiones independientes, por supuesto, utilizando el criterio del negocio.
El paquete arulesViz (Hahsler, 2017) también permite hacer visualizaciones interactivas. Solo requerimos emplear el argumento engine en la misma función plot(). Este argumento permite escoger qué “motor” de generación de gráficos se empleará. Ya debiste notar que los gráficos habían sido generados anteriormente con el paquete ggplot2. Podemos pedirle a esta función que emplee como “motor” el paquete plotly (Sievert, 2020). Por ejemplo, la siguiente línea de código genera la Figura 4.5:
Figura 4.5: Gráfico interactivo del soporte, confianza y lift de todas las reglas no redundantes encontradas por el algoritmo Apriori.
Este tipo de visualizaciones interactivas (Ver Figura 4.5) permiten al usuario interactuar con los datos. Juega un rato con este gráfico. Se pueden hacer zoom en partes del gráfico. Pasa el cursor por encima de un punto para ver la respectiva regla y sus métricas.
Esta visualización permite al tomador de decisiones ver tanto la regla de asociación como cada una de las tres métricas visualizadas; de esta manera es mucho más sencillo tomar decisiones.
4.3 Visualizando las reglas
Finalmente, para el negocio, lo más importante del MBA son las decisiones que se puedan tomar a partir de las reglas. Por esto, más importante que conocer las métricas de las reglas será conocer las reglas en sí. Una de las opciones para visualizar las reglas son los gráficos de coordenadas paralelas.
Este gráfico muestra los ítems en el eje vertical y el eje horizontal representa las posiciones en una determinada regla. El gráfico emplea una flecha cuya punta muestra al artículo consecuente. Las flechas sólo abarcan la distancia horizontal que sea necesaria para representar todos los elementos de la regla (antecedentes). En otras palabras, las reglas con menos elementos son flechas más cortas. El grosor de las flechas representa el soporte y la intensidad del color representa la confianza.
Empecemos con un ejemplo sencillo. Miremos el caso de las cuatro reglas de asociación que habíamos detectado con el algoritmo Apriori (umbral para el soporte de 0.01 y para la confianza de 0.8) con el ítem “HERB MARKER ROSEMARY” como antecedente (LHS).
## lhs rhs support confidence
## [1] {HERB MARKER ROSEMARY} => {HERB MARKER THYME} 0.01456182 0.9649123
## [2] {HERB MARKER ROSEMARY} => {HERB MARKER MINT} 0.01350278 0.8947368
## [3] {HERB MARKER ROSEMARY} => {HERB MARKER BASIL} 0.01244374 0.8245614
## [4] {HERB MARKER ROSEMARY} => {HERB MARKER PARSLEY} 0.01244374 0.8245614
## coverage lift count
## [1] 0.01509134 62.83575 55
## [2] 0.01509134 58.26588 51
## [3] 0.01509134 59.89170 47
## [4] 0.01509134 58.76167 47Nota que estas cuatro reglas tienen por construcción como antecedente únicamente el ítem “HERB MARKER ROSEMARY” y los consecuentes son itemsets de un ítem. El correspondiente gráfico de coordenadas paralelas se presenta en la Figura 4.6. Podemos ver cómo la regla que tiene como consecuente (RHS)“HERB MARKER THYME” tiene el mayor soporte (grosor de la flecha) y confianza (color más intenso).
Figura 4.6: Gráfico de coordenas paralelas para las reglas que tiene como antecedente el ítem HERB MARKER ROSEMARY.
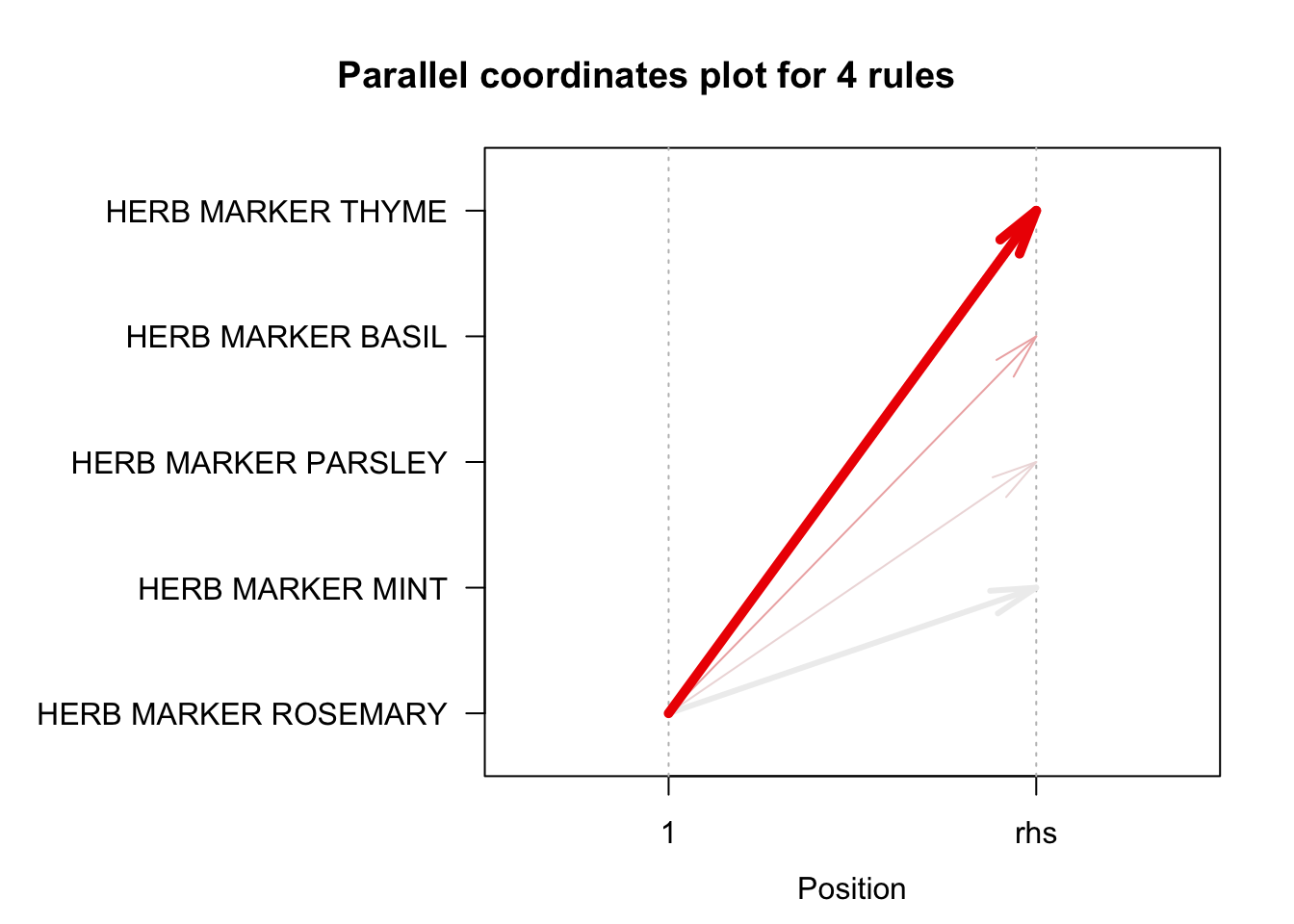
La Figura 4.6 traduce las cuatro reglas con antecedente “HERB MARKER ROSEMARY” en una lectura más accesible para la audiencia familiarizada con estas visualizaciones. Como se mencionó, la flecha más gruesa y de color rojo intenso conecta “ROSEMARY” con “THYME”. Esta flecha indica la regla de mayor soporte y confianza dentro del conjunto. Es decir, los compradores que adquieren el marcador de romero (“HERB MARKER ROSEMARY”) casi siempre añaden el de tomillo (“HERB MARKER THYME”) y lo hacen con una frecuencia relativamente alta en la base de datos de transacciones estudiada. Las flechas más tenues que apuntan a los marcadores de hierbas (“HERB MARKER”) de albahaca (“HERB MARKER BASIL”), perejil (“HERB MARKER PARSLEY”) y menta (“HERB MARKER MINT”) exhiben, respectivamente, soportes y confianzas decrecientes, lo que sugiere un vínculo comercial menos robusto, aunque todavía relevante. Para el negocio, esto implica priorizar el empaquetado o la exhibición conjunta de los marcadores de romero y tomillo; por ejemplo, un combo (bundle) con descuento o una ubicación contigua en góndola. Mientras que las combinaciones con albahaca, perejil y menta podrían aprovecharse en promociones secundarias o recomendaciones personalizadas orientadas a nichos más estrechos.
La Figura 4.6 fue generada con el siguiente código:
Para terminar de entender cómo se interpretan los gráficos de coordenadas paralelas veamos ahora el ejemplo de las reglas de asociación detectadas con el algoritmo Apriori (umbral para el soporte de 0.01 y para la confianza de 0.8) con el ítem “HERB MARKER THYME” como consecuente (RHS). Ver Figura 4.7.
Figura 4.7: Gráfico de coordenas paralelas para las reglas que tiene como consecuente el ítem HERB MARKER THYME.
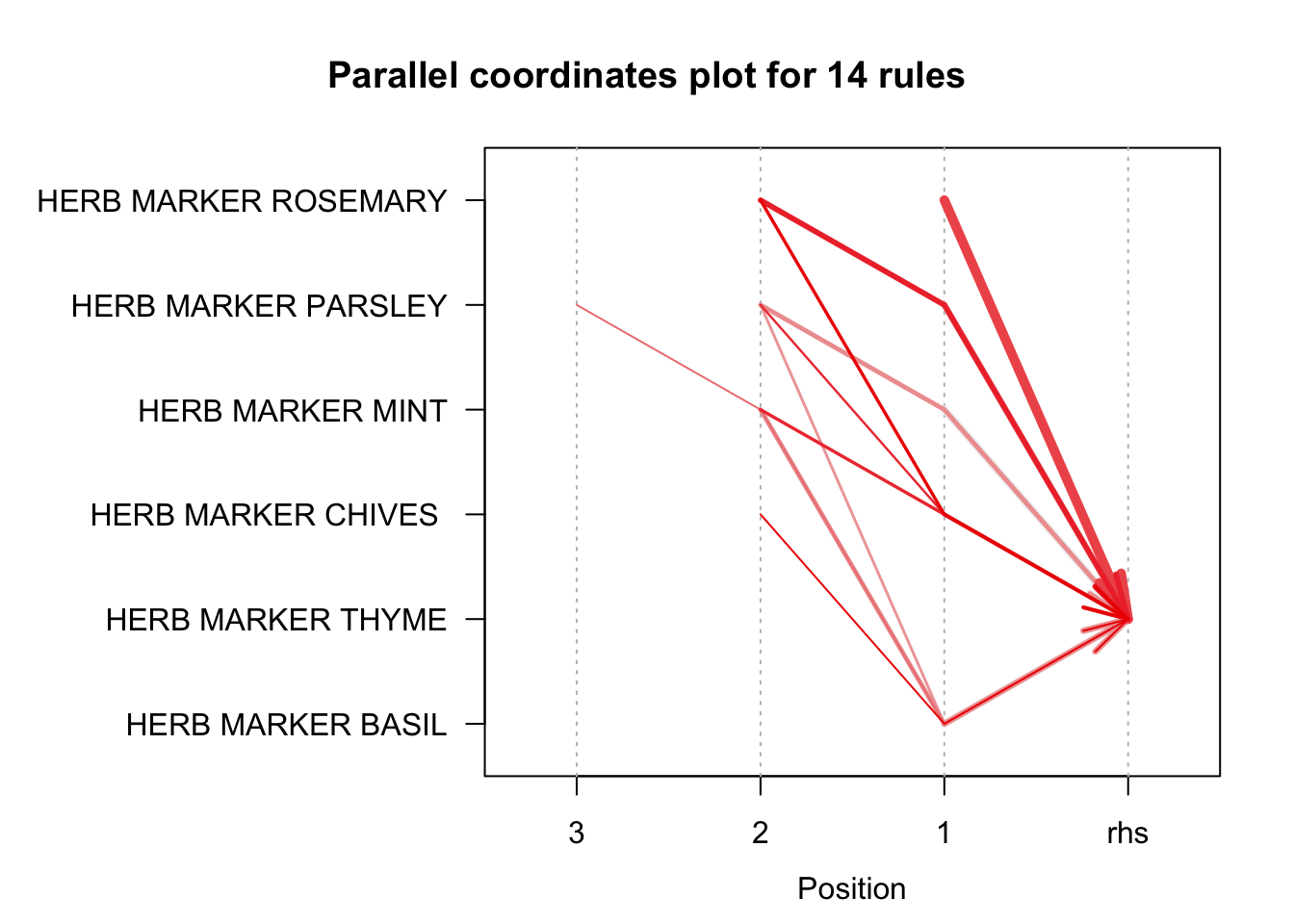
La Figura 4.7 muestra 14 reglas que confluyen en “HERB MARKER THYME” como consecuente (RHS). Las longitudes variables de las flechas evidencian el número de artículos que componen cada antecedente: las más cortas corresponden a reglas de un solo ítem. Por ejemplo, la flecha que sale de “HERB MARKER ROSEMARY” alcanza directamente la columna (LHS) Y las flechas más extensas involucran dos o tres marcadores; como por ejemplo, la regla que tiene 3 ítems como antecedente: “HERB MARKER PARSLEY”, “HERB MARKER MINT” y “HERB MARKER BASIL”42. El grosor y la intensidad del rojo reafirman la jerarquía observada anteriormente: la regla “HERB MARKER CHIVES” \(\rightarrow\) “HERB MARKER THYME” sobresale tanto en soporte como en confianza, seguida por la regla con antecedentes “HERB MARKER CHIVES” y “HERB MARKER ROSEMARY”. Las flechas tenues, aquellas que parten de “HERB MARKER PARSLEY”, “HERB MARKER MINT” o “HERB MARKER BASIL”, indican vínculos más débiles; no obstante, su presencia sugiere oportunidades de venta cruzada en segmentos de nicho, especialmente cuando el cliente ya ha mostrado preferencia por marcadores de hierbas múltiples. Así, este gráfico de coordenadas paralelas complementa la lectura estratégica: priorizar bundles simples de alto desempeño (la regla “HERB MARKER CHIVES” \(\rightarrow\) “HERB MARKER THYME”) y reforzar recomendaciones adicionales cuando el carrito contiene combinaciones menos frecuentes, elevando el ticket promedio sin sacrificar relevancia para el comprador.
La Figura 4.7 fue generada con el siguiente código43:
Intenta ahora interpretar el correspondiente a todas las reglas de asociación detectadas con el algoritmo Apriori (umbral para el soporte de 0.01 y para la confianza de 0.8) que se obtiene con el siguiente código 44:
Pese a que los gráficos de coordenadas paralelas son recursos efectivos para visualizar reglas de asociación, su comprensión demanda un cierto grado de conocimiento en técnicas cuantitativas y experiencia en el estudio de datos. Por lo tanto, si el público objetivo no ha desarrollado completamente estas habilidades, podría ser aconsejable elegir visualizaciones más intuitivas y fácilmente accesibles.
Una visualización de las reglas que puede ser más intuitiva son los grafos45. Podemos emplear el motor del paquete igraph (Csardi & Nepusz, 2006) para generar un grafo (method = “graph”). En este caso, los vértices se etiquetan con los nombres de los ítems, y los itemsets o reglas se representan como un segundo conjunto de vértices. Los elementos se conectan con los itemsets o reglas mediante flechas dirigidas. Las flechas que apuntan de los elementos a los vértices de las reglas indican los elementos del LHS y una flecha de una regla a un elemento indica el RHS. El tamaño y el color de los vértices representan medidas de interés como el lift y el soporte. La siguiente linea de código genera la Figura 4.8:
Figura 4.8: Gráfo para las reglas que tiene como consecuente el ítem HERB MARKER THYME.
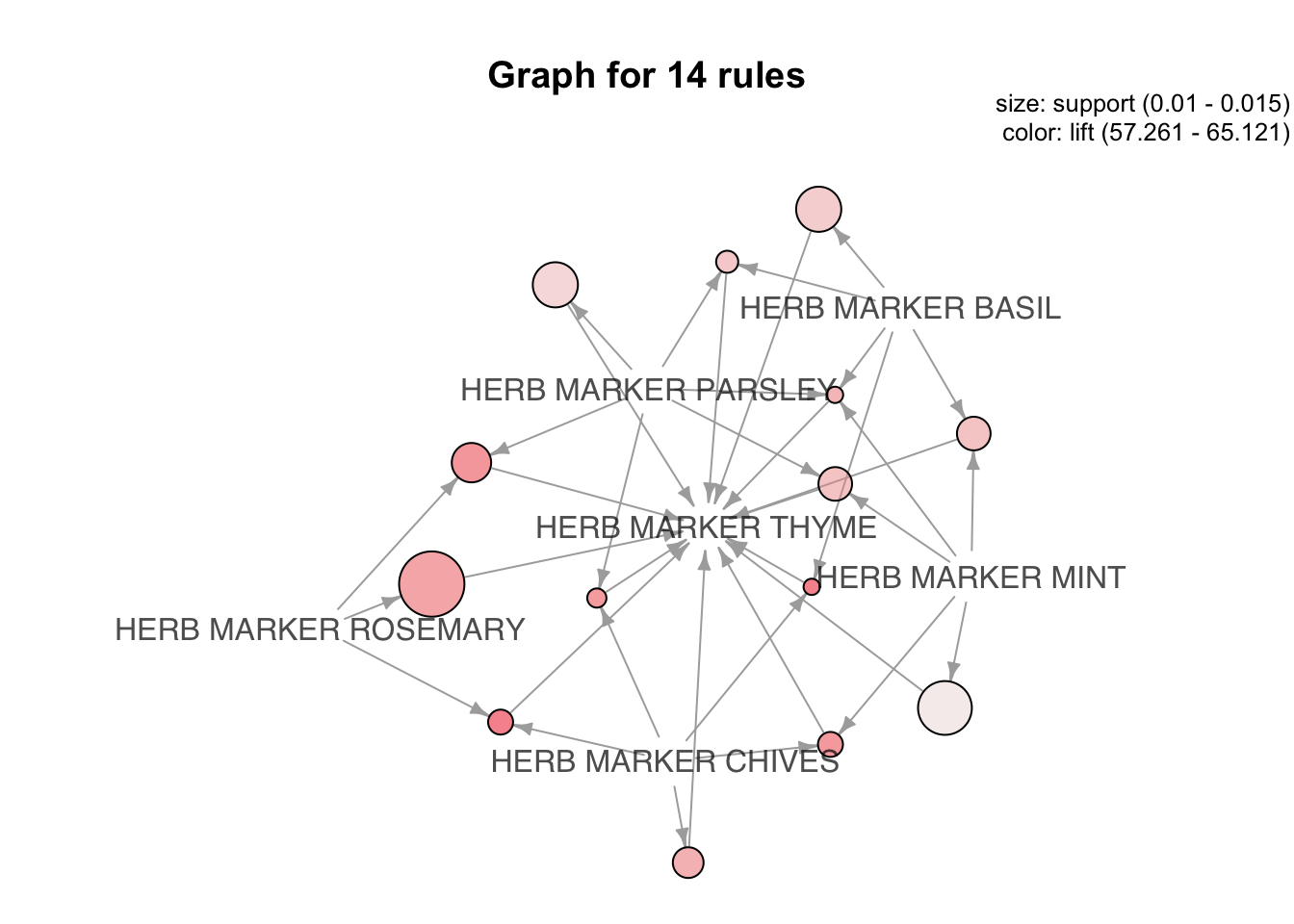
La Figura 4.8 representa en un grafo dirigido las 14 reglas que tienen como consecuente (RHS) “HERB MARKER THYME”. Como se mencionó arriba, cada círculo corresponde a un ítem y su tamaño refleja el soporte, mientras que la intensidad del rojo codifica el lift, que en este caso va de 57 a 65. El resultado es una red donde “HERB MARKER ROSEMARY” destaca por su diámetro al ser el antecedente con mayor frecuencia (soporte) y por un tono rojizo intermedio que denota un lift grande pero no extremo. Las flechas grises orientadas hacia “HERB MARKER THYME” hacen visible la direccionalidad LHS \(\rightarrow\) RHS. Las aristas (líneas que unen los círculos) más cortos provienen de antecedentes simples (por ejemplo, “HERB MARKER ROSEMARY” o “HERB MARKER CHIVES”), mientras que los ramales que convergen desde “HERB MARKER PARSLEY”, “HERB MARKER MINT” y “HERB MARKER BASIL” confirman reglas con múltiples ítems en el antecedente. Esta es otra forma de visualizar lo que ya habíamos visto en el gráfico de coordenadas paralelas (Ver Figura 4.7). No importa cómo lo visualicemos, los insights deben ser los mismos46.
En estos casos, quizás será mejor emplear una visualización interactiva que nos permita “jugar” con el grafo. Para lograr esto, solo tenemos que añadir un “motor” que nos permita generar grafos interactivos. Por ejemplo, podemos emplear engine = “htmlwidget”. Con esta aproximación podríamos visualizar las 14 reglas que tienen como consecuente el ítem HERB MARKER THYME; el siguiente código generó la Figura 4.9:
# grafo interactivo
# motor htmlwidget
plot(regla_thyme_rhs , method = "graph", engine = "htmlwidget") Figura 4.9: Grafo interactivo para las reglas que tiene como consecuente el ítem HERB MARKER THYME.
Esta visualización solo será interactiva en la versión web de este libro. El menú desplegable de la esquina superior izquierda de la Figura 4.9 permite seleccionar una regla o un elemento. Al seleccionar, por ejemplo, “HERB MARKER BASIL”, el ítem “HERB MARKER BASIL” y todas las reglas asociadas se resaltan en el grafo. Del mismo modo, al seleccionar la regla 2, se resalta esta regla y todos los elementos asociados. Esta forma de filtrar elementos y reglas puede ser útil, especialmente cuando el número de reglas es muy grande. ¡Juega un rato con esta visualización!
Pero hay que tener cuidado con los grafos porque tienden a congestionarse a medida que aumenta el número de reglas. Por lo tanto, es mejor visualizar un número relativamente pequeño de reglas con los grafos.
Por ejemplo, graficar en un grafo las 294 reglas de asociación detectadas con el algoritmo Apriori (umbral para el soporte de 0.01 y para la confianza de 0.8) sería poco útil. Pero podemos ordenar las reglas según una métrica específica y visualizarlas con las mayores métricas. Por ejemplo, intenta el siguiente código para visualizar 30 reglas47:
Ahora intenta con 60 reglas:
Podemos guardar el grafo interactivo empleando la función saveWidget() del paquete htmlwidgets (Vaidyanathan et al., 2022). En este caso solo tenemos que guardar el grafo en un objeto y emplear la función para guardarlo en un archivo de formato .html. Por ejemplo:
# Cargar el paquete
library(htmlwidgets)
#guardar el grafo en un objeto
grafo <- plot(head(sort(reglas, by = "support"),60)
, method = "graph", engine = "htmlwidget")
#Grabando el archivo
saveWidget(grafo , file = "reglas_60_grafo.html")¡Esta visualización interactiva de los resultados en forma de grafo puede ser muy útil para la toma de decisiones! No obstante, sigue requiriendo cierto grado de sofisticación cuantitativa del tomador de decisiones. En algunas ocasiones, será más conveniente entregar toda la información de las reglas de asociación encontradas para que el tomador de decisiones tenga toda la información relevante. La función inspectDT() del paquete arulesViz (Hahsler, 2017) genera un widget HTML que permite jugar de forma interactiva con el conjunto de reglas de asociación que tengamos guardadas en un objeto, presentándolo en forma de cuadro interactivo.
Por ejemplo, el siguiente código genera una tabla en formato .html que permite interactuar con las reglas.
Figura 4.10: Widget con reglas de asociación generadas con el algoritmo Apriori.
Este tipo de tabla interactiva permite al usuario interactuar con los datos. Nota que esta tabla también la puedes grabar como un archivo .html empleando la función saveWidget() que vimos anteriormente.
Otra opción para entregar los resultados al usuario, pero un poco más complicada de distribuir48, es emplear el paquete shiny49 (Chang et al., 2021) y la función ruleExplorer(). ¡Intenta el siguiente código y juega con el resultado!
# Cargar el servidor shiny
ruleExplorer(reglas)
# Para ver el servidor, pega la dirección correspondiente en un navegador
# busca la dirección des pues del texto "Listening on" copia lo que sigue
# debe iniciar por "http://"Ahora estamos listos para interpretar y diseñar estrategias de mercadeo. ¡La imaginación es el límite!
4.4 Comentarios finales
Este capítulo discute la visualización de los resultados del MBA, el insumo principal para entregar a quienes toman las decisiones en la organización. Así, la tarea de visualización consiste en usar gráficos que “cuenten” la historia de lo observado en las canastas de compras. Como se ha discutido en capítulos anteriores, aunque son roles diferentes, el científico de datos y el analytics translator deben trabajar de manera coordinada.
Este capítulo le permitirá al científico de datos saber cómo realizar la codificación para la visualización de los resultados. El científico de datos debe entender las preguntas del negocio para generar visualizaciones coherentes con estas necesidades. En el caso del analytics translator, el contenido de este capítulo le permitirá conocer qué tipo de visualización solicitar al científico de datos. El analytics translator debe entender las posibilidades que hay para visualizar los resultados de tal forma que facilite la toma de decisiones.
El MBA es una herramienta del business analytics que permite tomar decisiones a partir de datos que surgen de las transacciones habituales en los consumidores de un canal minorista. Teniendo en cuenta las decisiones de negocio que se esperan tomar, el MBA crea reglas de asociación que facilitan tomar decisiones basados en datos. Es decir, el MBA supone que el minorista ha consolidado una base de datos con las transacciones de los clientes y que tiene una pregunta estratégica de negocio que permite enfocar las reglas de asociación. El MBA resuelve múltiples preguntas de negocio (ver sección 1.1) que impliquen encontrar la coocurrencia de productos en las canastas de compra.
Las herramientas discutidas en este libro pueden ser utilizadas por científicos de datos y analytics translators para pasar de datos transaccionales a la toma de decisiones empleando el MBA. Los científicos de datos deben entender las preguntas de negocio para generar el análisis pertinente y las visualizaciones que permitan comunicar los resultados obtenidos. Los analytics translators deben entender las potencialidades y limitaciones del MBA para poder traducir las preguntas de negocio al equipo de científicos de datos. Así mismo, al culminarse el MBA será necesario escoger qué tipos de visualizaciones solicitar a los científicos de datos para facilitar la toma de decisiones. Como hemos visto a lo largo de este libro, el MBA es una herramienta poderosa para tomar decisiones basadas en datos en un entorno minorista.
Las aplicaciones del MBA son muchas, ¡la imaginación es el límite!
En el siguiente capítulo veremos un caso completo de estudio aplicado a datos de una panadería en línea de Edimburgo. Ese capítulo te podrá dar ideas de cómo aproximarte a tu primera pregunta de negocio que se pueda responder con la tarea de Encontrar Reglas de Asociación.
Referencias
Recuerda que cuando tenemos funciones que tienen el mismo nombre en diferentes paquetes, típicamente estas están diseñadas para reaccionar distinto de acuerdo a la clase del objeto que se use en el argumento.↩︎
Este tipo de visualización no es recomendable; en la mayoría de las situaciones es muy confuso.↩︎
Esto lo puedes constatar con la linea de código
inspect(regla_thyme_rhs, by = "confidence"), es la última regla.↩︎Por razones de espacio no se reporta esta visualización.↩︎
Si visualizas todas las reglas, tu computador se demorará mucho y en algunos casos colapsará. Por eso filtramos las reglas más importantes según el soporte.↩︎
Si no estás familiarizado con los grafos, puedes encontrar una introducción al tema en Alonso & Carabali (2019).↩︎
Por un lado, enfatizar la coexhibición “HERB MARKER ROSEMARY” y “HERB MARKER THYME” en el punto de venta por su alta frecuencia y lift robusto. Y por otro lado, usar recomendaciones orientadas a nichos para “HERB MARKER MINT”, “HERB MARKER BASIL” o “HERB MARKER PARSLEY” cuando el cliente ya lleva varios marcadores en su carrito, optimizando el cross-selling sin saturar al comprador↩︎
Por razones de espacio no se reporta esta visualización.↩︎
En este caso tendremos que instalar un servidor shiny, pues se necesita que R esté corriendo para que la app de shiny esté corriendo.↩︎
Este es un paquete de R que permite generar rápidamente aplicaciones web.↩︎