7 Modelo DBSCAN
Objetivos del capítulo
Al finalizar este capítulo, el lector estará en capacidad de:
- Explicar en sus propias palabras la lógica detrás de la construcción de un clúster empleando el algoritmo DBSCAN.
- Construir en R clústeres empleando el algoritmo DBSCAN.
7.1 Introducción
En el Capítulo anterior continuamos con el estudio de algoritmos de clústering particionado basado en centroides. Con el estudio de los algoritmos basados en medoides del Capítulo 6 ya tenemos una lista grande algoritmos. Recordemos que hemos estudiado los siguientes modelos:
- AGNES (algoritmo jerárquico aglomerativo)
- DIANA (algoritmo jerárquico de división)
- k-means (algoritmo particionado basado en centroides)
- PAM (algoritmo particionado basado en medoides)
- CLARA (algoritmo particionado basado en medoides)
En este Capítulo estudiaremos un algoritmo de clústering particionado basado en densidad. En general, este tipo de algoritmos basado en densidad se caracteriza por identificar regiones de alta densidad de individuos separadas por regiones de baja densidad en el espacio de datos (Ver Figura 7.1).
Figura 7.1: Clústeres particionados basados en densidad
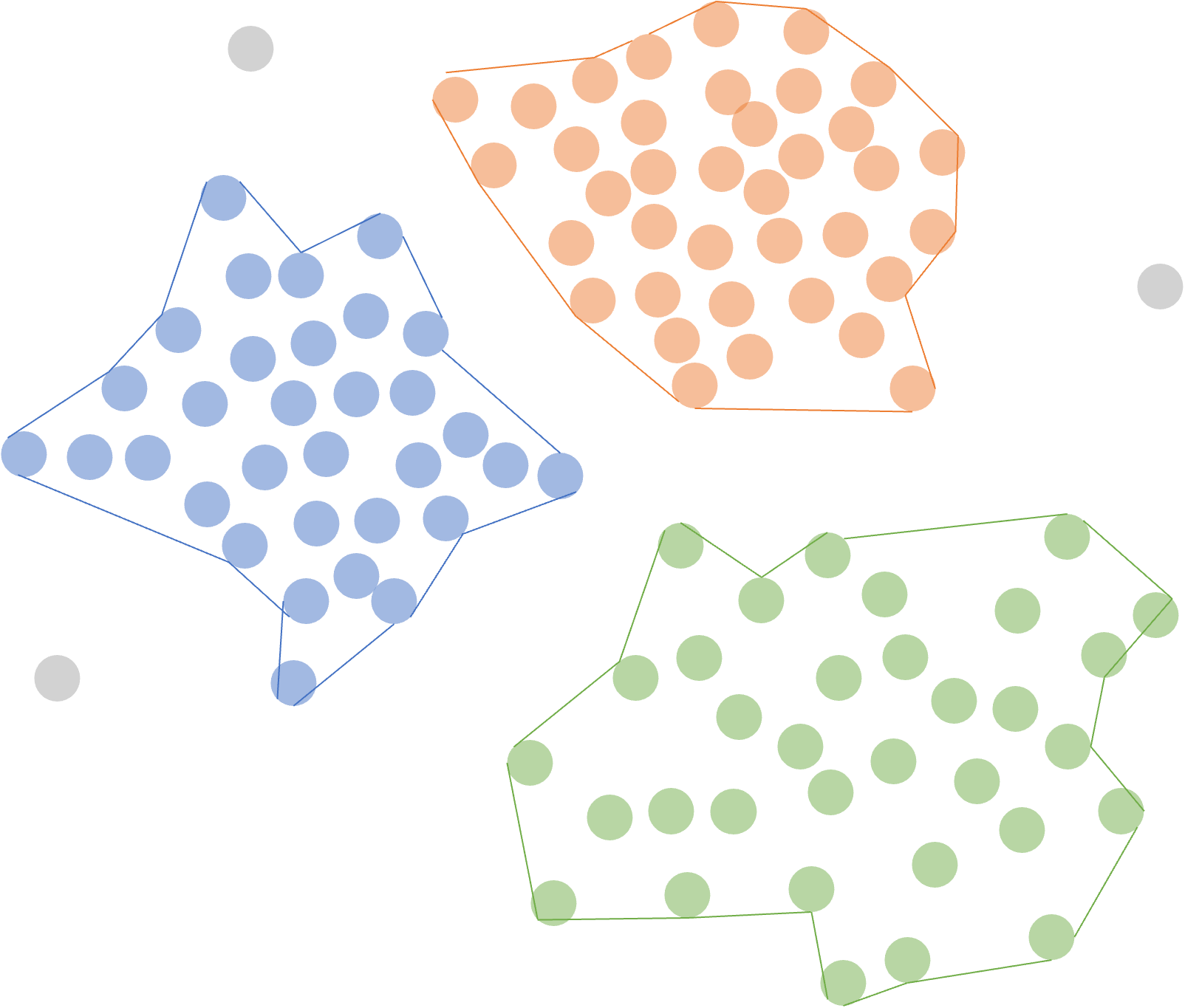
El algoritmo DBSCAN (Density-Based Spatial Clustering of Applications with Noise) es uno de los enfoques más populares en esta categoría y se destaca por su capacidad para identificar grupos de formas arbitrarias y su robustez ante ruido en los datos67 y datos atípicos.
7.2 El algoritmo DBSCAN
DBSCAN fue propuesto por Ester et al. (1996) como una solución a la dificultad de encontrar conglomerados de forma arbitraria en conjuntos de datos con diferentes densidades y formas. La primera diferencia de este con los algoritmos de clústering particionado estudiados hasta ahora (k-means, PAM y CLARA), es que DBSCAN no necesita especificar el número de conglomerados. DBSCAN detecta automáticamente el número de conglomerados basándose en los datos y parámetros de entrada. Otra diferencia con los algoritmos estudiados hasta ahora (particionados y jerárquicos), es que DBSCAN puede encontrar clústeres de formas arbitrarias. Por ejemplo, en la Figura 7.2 (primera fila) podemos observar cómo DBSCAN puede detectar un clúster rodeado por otro clúster, mientras que un algoritmo como el k-means divide el espacio de una manera lineal. También puede encontrar formas no lineales, como en la segunda y tercera fila de la Figura 7.2.
Figura 7.2: Ejemplo 1 de los diferentes clústeres que pueden formar DBSCAN y k-means apartir de la misma muestra de individuos con dos características

No obstante, aunque el algoritmo DBSCAN puede encontrar formas no tradicionales en algunas ocasiones puede detectar los mismos clústeres que detectarían otros algoritmos como el k-means (Ver línea uno de la Figura 7.3). Por otro lado, cuando los individuos se encuentran relativamente concentrados (Ver línea uno de la Figura 7.3) es poco probable que DBSCAN pueda construir grupos, como sí lo hacía el algoritmo k-means.
Figura 7.3: Ejemplo 2 de los diferentes clústeres que pueden formar DBSCAN y k-means a partir de la misma muestra de individuos con dos características

Por otro lado, DBSCAN puede tratar el ruido y los valores atípicos. Todos los valores atípicos serán identificados y marcados sin ser clasificados en ningún clúster (Ver línea uno de la Figura 7.4). Por lo tanto, DBSCAN también puede utilizarse para la detección de anomalías (detección de valores atípicos) (Kassambara, 2017).
Figura 7.4: Algoritmo DBSCAN detectanto outliers

Antes de describir los pasos del algoritmo DBSCAN, tenemos que definir dos parámetros: eps (\(\epsilon\)) y minPts. eps (\(\epsilon\)) que representan el radio máximo del vecindario; en otras palabras, es la distancia máxima entre dos puntos para que se consideren vecinos y por tanto pertenezcan al mismo grupo. Esto corresponde al vecindario \(\epsilon\) (\(\epsilon\)-neighborhhood) de un determinado punto central (core point). Por otro lado, minPts es el número mínimo de puntos que deben estar dentro de la vecindad de un punto para que este sea considerado un punto central y, por tanto, se configure un clúster (incluyendo el mismo punto).
Intuitivamente, cada individuo en la muestra que tenga un número de vecinos (en el vecindario \(\epsilon\)) igual o mayor minPts será marcado como un punto central (Ver Figura 7.5). Por otro lado, si un individuo \(w\) tiene un número de vecinos inferior a minPts, pero pertenece al vecindario \(\epsilon\) (\(\epsilon\)-neighborhood) de otro punto, entonces \(w\) será denominado un punto de frontera (border point) (Ver Figura 7.5). Y si un punto no es punto central (core point) ni uno en la frontera (border point), entonces será denominado ruido (noise point) o outlier (Ver Figura 7.5).
Figura 7.5: Clasificación de individuos en el algoritmo DBSCAN con minPts = 6

Como lo hemos hecho en los capítulos anteriores, veamos los pasos del algoritmo para entenderlo mejor. Los pasos para realizar un clústering particionado usando el algoritmo DBSCAN, son:
Marcar todos los individuos como “no visitados”.
Seleccionar un individuo al azar entre los puntos no visitados anteriormente y calcular la distancia de este con respecto a los demás individuos.
Si se encuentra que el individuo tiene un número igual o superior de vecinos a minPts que se encuentren a una distancia menor o igual a eps (\(\epsilon\)) (el individuo es un punto central), crear un nuevo clúster y marcar al individuo como visitado.
Agregar al clúster todos los individuos vecinos del individuo inicial que no hayan sido visitados y que se encuentren dentro de la distancia eps (\(\epsilon\)).
Repetir los pasos 3 y 4 para todos los vecinos del individuo inicial, hasta que no hayan más individuos que agregar al clúster.
Marcar el individuo inicial como “visitado”.
Repetir pasos 2 a 5 para todos los individuos no visitados, hasta que no queden individuos sin visitar.
Asignar a cada punto la membrecía al clúster en el que fue clasificado. Para los individuos que no se encuentran dentro de ningún clúster se marcan como ruido o outliers y se les asigna una etiqueta especial.
El algoritmo DBSCAN no requiere la definición previa del número de clústeres, dado que el número óptimo de clústeres \(q\) es un resultado del este algoritmo. Antes de emplear la función, es importante reconocer que, en este caso, el número de clústeres óptimo (\(q\)) es seleccionado en el mismo proceso de maximización.
En este orden de ideas, no tiene mucho sentido emplear la silueta promedio para escoger el número óptimo de clústeres, procedimiento que sí tenía sentido para todos los modelos de clústering estudiados hasta el momento68.
Por otro lado, sí es posible encontrar el valor óptimo del parámetro eps (\(\epsilon\)). Chen et al. (2020) sugieren emplear la media de las distancias de cada individuo a sus \(k\) vecinos más cercanos (distancia kNN). Esto implica calcular la distancia kNN para cada individuo y diferentes valores del parámetro eps y posteriormente calcular la suma cuadrada de las distancias kNN. Empleando ese resultado podemos graficar, para los diferentes valores de eps, el número mínimo de observaciones que se encontraron en el ejercicio de clusterización. Posteriormente, se puede identificar por medio del método del “codo” el valor óptimo de eps. En otras palabras, buscar el punto en la gráfica donde la pendiente cambia significativamente. En la siguiente sección estudiaremos cómo implementar este algoritmo en R.
7.3 Implementación del algoritmo DBSCAN en R
Este algoritmo se puede implementar en R por medio de la función dbscan() del paquete dbscan (Hahsler et al., 2019). Pero antes de emplear esta función es necesario conocer cuál es el valor óptimo del parámetro eps. La propuesta de Chen et al. (2020) se puede implementar en R empleando la función n_clusters_dbscan() del paquete parameters. Esta función es similar a la función n_clusters_silhouette() que empleamos en el Capítulo 6.
Esta función tiene los siguientes argumentos:
donde:
x: Objeto con datos de clase data.frame.
standardize: Si es TRUE se estandarizarán los datos, este es el valor por defecto.
include_factors: Si es TRUE, las variables de clase factor se convierten en objetos numéricos para ser incluidos en los datos, para determinar el número de clústeres. Por defecto, es igual a FALSE; es decir, se eliminan las variables que sean de clase factor. Esto se hace porque la mayoría de los métodos que determinan el número de conglomerados solo funciona con variables cuantitativas.
min_size: El número mínimo de individuos (incluyendo al mismo individuo) requeridos en el vecindario \(\epsilon\) (\(\epsilon\)-neighborhood) para ser considerado como un punto central (core point). Por defecto, el valor es el 10% de la muestra (min_size = 0.1). Si se emplea un entero, este será el número de observaciones. Equivale al parámetro minPts.
eps_range: El rango sobre el cuál se evaluarán los posibles valores del parámetro eps.
method: El método para escoger el parámetro eps óptimo. En nuestro caso empleemos method = “SS” para que se calcule la suma cuadrada.
distance_method: El tipo de distancia a calcular. Este elemento es pasado a la función dist(). Por defecto el método es “euclidean”; los otros posibles valores son “maximum”, “manhattan”, “canberra”, “binary” y “minkowski”. No obstante, para el caso del algoritmo DBSCAN, no se encuentra habilitada la opción para otra distancia.
El valor óptimo del parámetro eps (\(\epsilon\)) para el algoritmo DBSCAN y el método de la distancia kNN lo podemos encontrar con el siguiente código, empleando nuestros datos ya estandarizados (datos_est) y la distancia euclidiana.
res_dbscan_knn <- n_clusters_dbscan(datos_est,
standardize = FALSE,
eps_range = c(0.001, 3),
min_size = 5,
distance_method = "euclidean",
method = "SS")Los resultados del eps óptimo lo podemos visualizar imprimiendo el resultado en la consola o por medio de la Figura 7.6
## The DBSCAN method, based on the total clusters sum of squares, suggests that the optimal eps = 0.551836734693878 (with min. cluster size set to ), which corresponds to 16 clusters.Figura 7.6: Seleccionando el valor óptimo del parámetro eps por medio de la distancia kNN
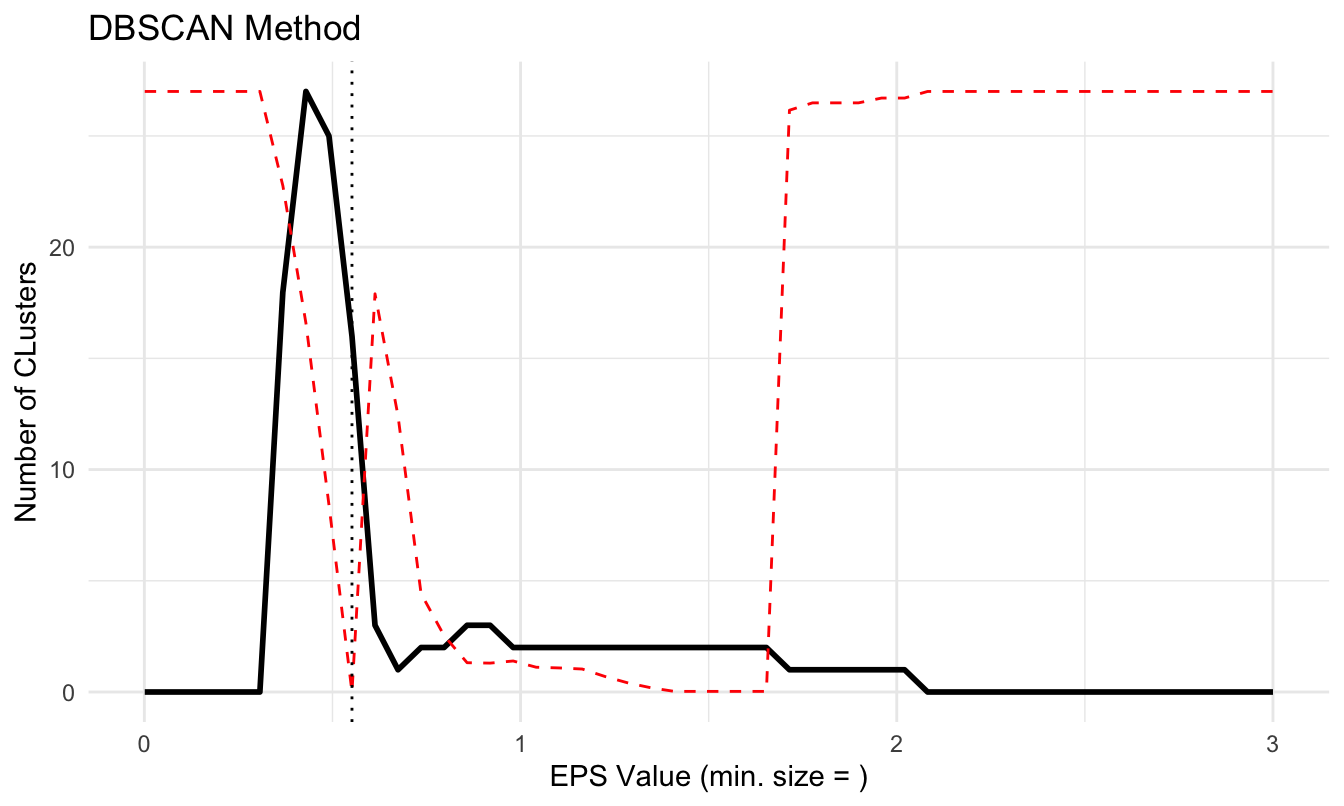
El resultado que minimiza la suma de las distancias kNN corresponde a un 0.5518367 Noten que en este caso esto implica 16 clústeres.
El valor óptimo del parámetro eps (\(\epsilon\)) se puede extraer de la siguiente manera:
## [1] 0.5518367Si bien, en este caso no tiene mucho sentido calcular la membrecía de cada individuo, pues no tenemos clústeres, continuaremos el ejercicio por razones pedagógicas.
La partición de los datos se puede realizar empleando la función dbscan() del paquete dbscan (Hahsler et al., 2019). Esta función solo requiere como argumentos:
x: Los datos estandarizados o una matriz de proximidad69.
eps: El parámetro (\(\epsilon\)) que representa el radio máximo del vecindario.
minPts: El número mínimo de individuos (incluyendo al mismo individuo), requeridos en el vecindario \(\epsilon\) (\(\epsilon\)-neighborhood) para ser considerado como un punto central (core point).
En nuestro caso:
# Instalar el paquete si no se tiene
# install.packages("dbscan")
# Cargar el paquete
library("dbscan")
# DBSCAN
res_DBSCAN <- dbscan::dbscan(x = datos_est, eps = eps_opt,
minPts = 5)Las membrecías se pueden encontrar fácilmente con el siguiente código:
## [1] 0 0 0 0 0 1Por otro lado, si bien emplear la silueta para escoger el número óptimo de grupos para el algoritmo DBSCAN no tiene sentido, es posible calcular la silueta promedio. Y si es el caso, puede emplearse para comparar esta aproximación con otros algoritmos (realizar la validación del clúster).
En todo caso, será importante recordar que la silueta promedio casi siempre favorecerá modelos como los jerárquicos y particionados basados en centroides (k-means, PAM y CLARA) que a modelos como el DBSCAN. Esto se debe a que la aproximación de DBSCAN y GMM permiten crear conglomerados “largos y delgados” y hasta “envolver otros conglomerados”; es decir, por construcción no intentan optimizar las distancias intra e inter conglomerados, que es lo que mide la silueta. Y por ejemplo, k-means sí intenta, más o menos, optimizar estas dos cantidades.
En nuestro caso, cada silueta se podría calcular con el siguiente código:
# Calcular las siluetas individuales
sil_DBSCAN <- silhouette(res_DBSCAN$cluster, dist(datos_est))
# Calcular la silueta promedio
mean(sil_DBSCAN[,3])## [1] -0.09057502
7.4 Otro ejemplo
Para mostrar las bondades de este algoritmo, empleemos un ejemplo con datos del paquete factoextra (Kassambara & Mundt, 2020). Estos datos tienen una distribución no lineal que permite entender mejor las bondades de DBSCAN. Carguemos los datos en el objeto multishapesy solo empleemos las dos primeras variables. Estos datos ya están estandarizados.
# Cargar el paquete
library(factoextra)
# Cargar los datos
data("multishapes")
# Seleccionar las dos primeras variables
multishapes <- multishapes[, 1:2]La Figura 7.7 nos permite observar la no linealidad de los datos; algo similar a lo presentado en la Figura 7.2 (primera fila).
Figura 7.7: Datos del ejemplo 2
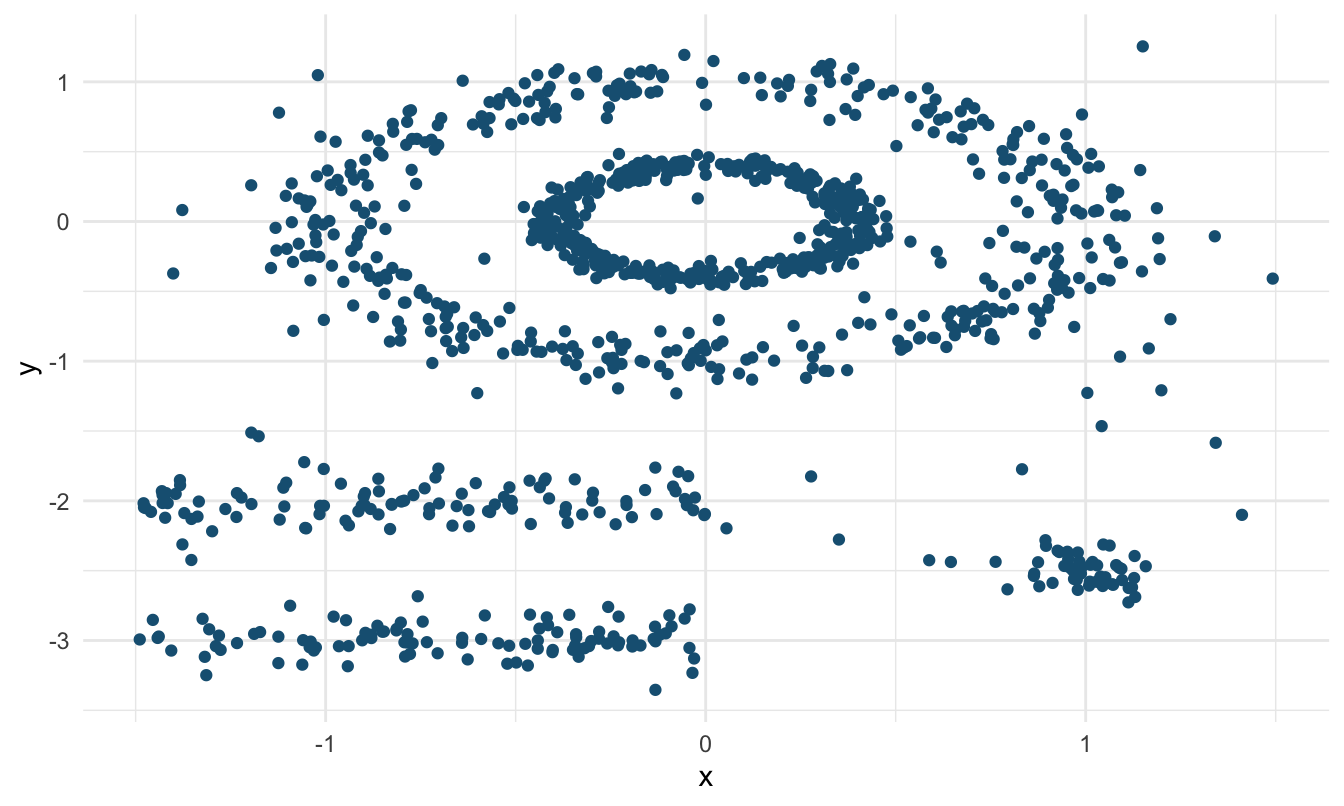
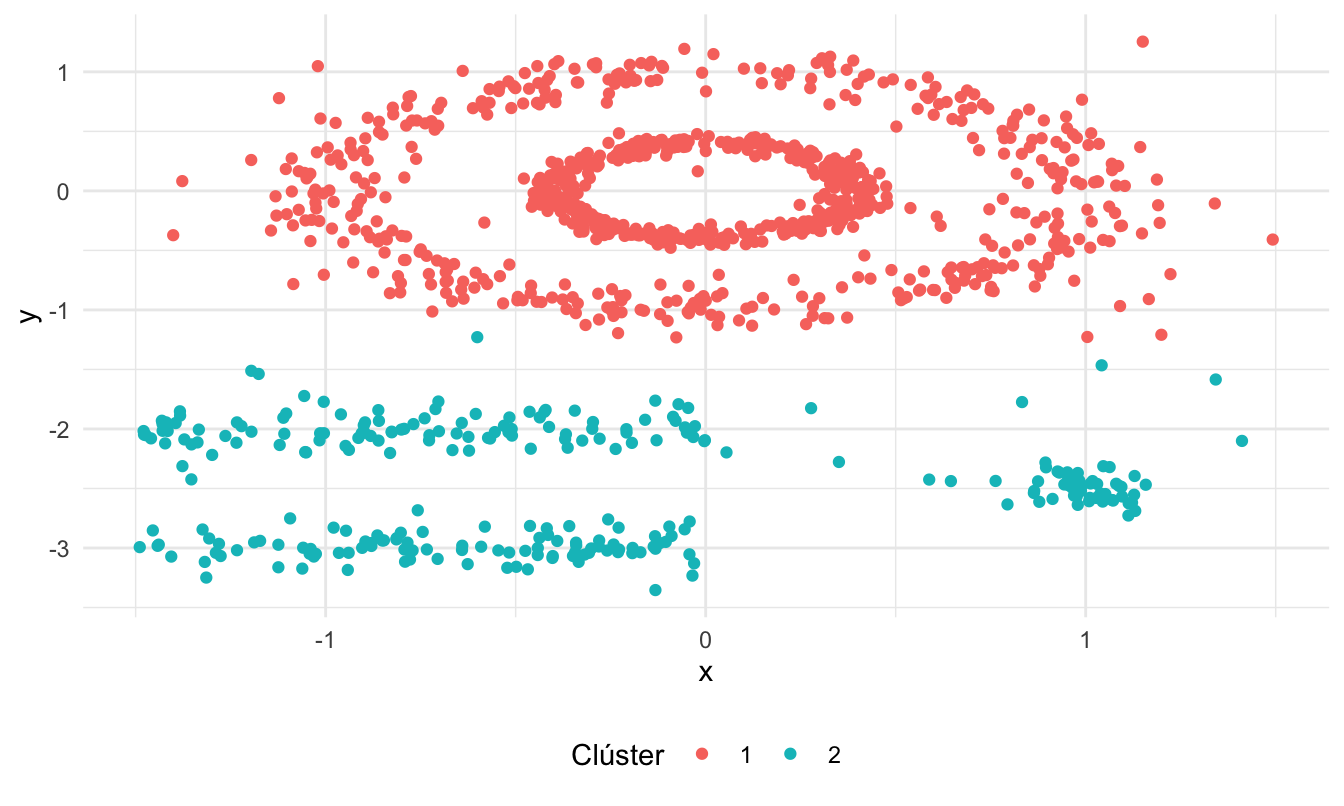
Para poder comparar los resultados de DBSCAN, empleemos el algoritmo k-means. Puedes encontrar que, empleando la distancia euclidiana y el criterio de la silueta, el número óptimo de clústeres será 2 (el código no se presenta intencionalmente). Los datos y sus respectivas membrecías se reportan en la Figura 7.8. Con el algoritmo k-means encontramos 2 clústeres.
Figura 7.8: Partición de los datos del ejemplo 2 empleando k-means
Ahora empleemos el algoritmo DBSCAN. Primero optimicemos el parámetro eps.
res_eje2_dbscan <- n_clusters_dbscan(multishapes,
standardize = FALSE,
eps_range = c(0.001, 3),
distance_method = "euclidean",
min_size = 5,
method = "SS")El valor óptimo de eps es 0.1234082 lo que implicará 7 clústeres.
En la Figura 7.9 se presenta la partición generada por el algoritmo DBSCAN. El clúster cero corresponde a los outliers marcado por el algoritmo.
Figura 7.9: Partición de los datos del ejemplo 2 empleando DBSCAN
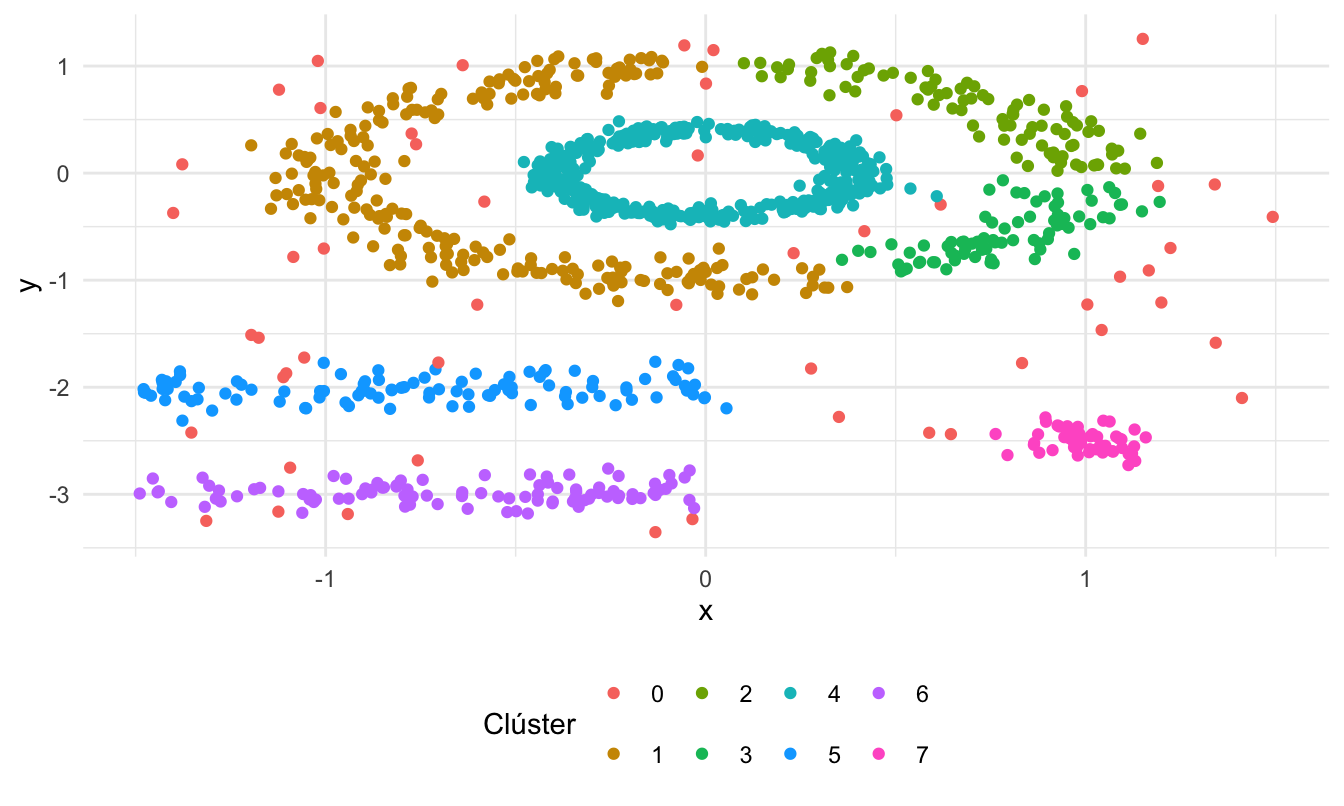
Observando los resultados, parece ser mucho mejor emplear DBSCAN que el algoritmo k-means para generar la partición de los datos. No obstante, al emplear la silueta para realizar la comparación de los dos algoritmos, encontraremos (¡Intenta reproducir estos resultados!) que la silueta promedio para la partición empleando k-means es de 0.418 y para el caso del agrupamiento generado por DBSCAN la silueta promedio es de 0.307. Esto nos lleva, de nuevo, a la observación que hacíamos más arriba. La silueta promedio, por su construcción, tiende a favorecer particiones lineales como k-means y casi siempre una aproximación como DBSCAN será penalizada fuertemente por esta métrica. Por eso, es importante la intervención del científico de datos en el momento de construcción de los clústeres. La selección automática de la mejor aproximación para particionar los datos puede llevarnos a estas contradicciones. Es importante entender en qué contexto nos encontramos, y si tiene o no sentido emplear determinada métrica para tomar esta decisión. En este ejemplo, es evidente que la silueta promedio no es la mejor opción para seleccionar la “mejor” aproximación para particionar los datos.
7.5 Comentarios finales
En este capítulo hemos estudiado un tipo de clústering particionado basado en la densidad de los datos: DBSCAN. El algoritmo DBSCAN busca, de manera iterativa, aquellos individuos que se encuentran en un radio inferior a una distancia previamente establecida (parámetro eps). Con esta búsqueda, arma los conglomerados de acuerdo a dónde exista mayor densidad de individuos. De hecho este algoritmo depende de dos parámetros: el radio (distancia) para establecer los vecinos (eps) y el número mínimo de individuos que deben estar dentro de la vecindad, para que el individuo se configure en un clúster (minPts).
Los resultados de este algoritmo son muy sensibles a la escogencia de estos parámetros, en especial del parámetro eps. Por esta razón, también estudiamos una estrategia para fijar, a partir de los datos, este parámetro.
Finalmente, es importante recordar que el algoritmo DBSCAN es una herramienta más para realizar la tarea de hacer clústeres, que debes tener en tu caja de herramientas. Como las otras herramientas que hemos estudiado, DBSCAN no es una solución mágica que funcione en todos los casos, pero tiene algunas ventajas significativas sobre otros algoritmos de agrupamiento.
Por ejemplo, DBSCAN no requiere que especifiques el número de clústeres por adelantado. Esto puede ser una gran ventaja, ya que a menudo es difícil saber cuántos clústeres hay en un conjunto de datos. DBSCAN encontrará automáticamente el número de clústeres que mejor se ajuste a los datos.
DBSCAN es capaz de encontrar clústeres de formas arbitrarias. Esto es importante, ya que los clústeres en el mundo real no siempre son bonitos y redondos. DBSCAN puede encontrar clústeres que sean alargados, ramificados o incluso con forma de anillo. DBSCAN también es relativamente eficiente. Esto significa que se puede ejecutar en conjuntos de datos grandes sin tomar demasiado tiempo.
Sin embargo, DBSCAN también tiene algunas desventajas. Como lo acabamos de mencionar, DBSCAN puede ser sensible a la elección de los parámetros. Por construcción, DBSCAN puede tener dificultades para encontrar clústeres de baja densidad.
En general, DBSCAN es una herramienta poderosa para el agrupamiento de datos. Es importante ser consciente de sus ventajas y desventajas para poder utilizarlo de forma eficaz. En el siguiente capítulo continuaremos nuestro análisis de algoritmos para construir clústeres. Estudiaremos una filosofía totalmente diferente a la construcción de agrupaciones.
Referencias
En la jerga del científico de datos, el término “ruido” se refiere a los datos que no siguen el patrón general o la estructura subyacente de los datos. En el contexto de la tarea de clústering, el ruido se refiere a los individuos que no pertenecen claramente a ningún clúster o que pueden interferir con la identificación de clústeres con mayor definición. ↩︎
Recuerda que en el caso de los algoritmos particionados, empleamos el algoritmo para diferentes números de clústeres y se selecciona el número de clústeres óptimo (\(q\)) con métricas o con la silueta promedio. Para el caso de los algoritmos jerárquicos, éstos encuentran todos los posibles clústeres. Con las métricas o con la silueta decidimos por dónde podar el árbol jerárquico (\(q\)).↩︎
Si se quisiera emplear otro tipo de distancia diferente a la euclidiana, esto se puede realizar empleando una matriz de proximidad con la función dist(). ↩︎