2 Generalidades y métricas en el clústering
Objetivos del capítulo
Al finalizar este capítulo, el lector estará en capacidad de:
- Explicar en sus propias palabras los elementos necesarios para construir clústeres.
- Explicar en sus propias palabras las distancias más comunes que se emplean en la construcción de conglomerados.
- Explicar en sus propias palabras la diferencia entre clústeres particionados y no particionados.
- Explicar en sus propias palabras cómo se puede seleccionar el número de clústeres.
En el Capítulo 1 discutimos cómo la tarea de clústering hace parte de la caja de herramientas de un científico de datos. También estudiamos la relación de esta tarea con los cuatro tipos de analítica. En este Capítulo nos concentraremos en estudiar la intuición detrás de esta tarea. Los elementos que son comunes a los algoritmos de clústering, y a cómo evaluar la bondad del resultado de un ejercicio de clústering dado que no se cuenta con un valor “real contra el cual comparar” (Ver discusión al final del Capítulo 1).
2.1 La intuición detrás de los algoritmos de clústering
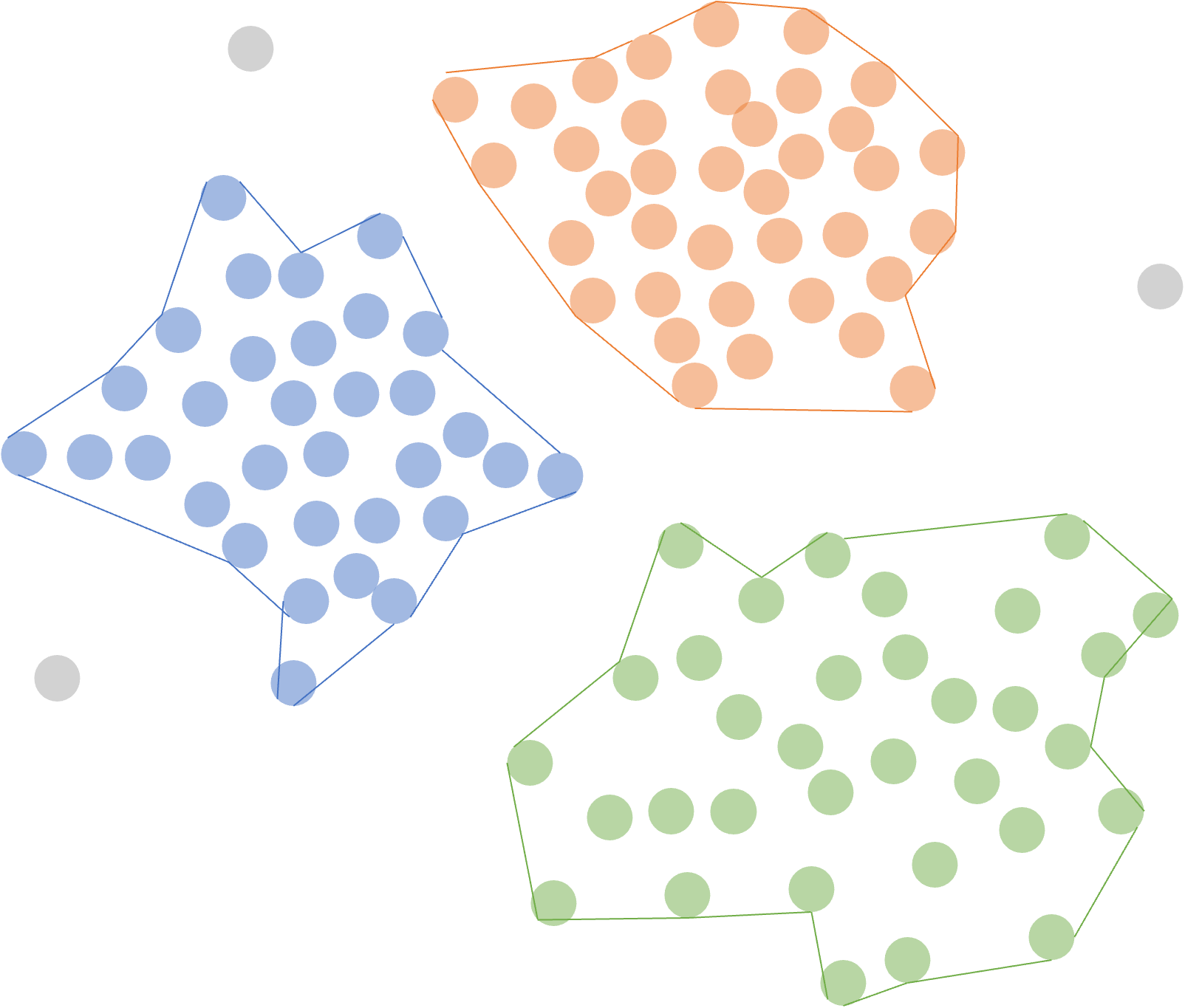
Para hacernos una mejor idea de la tarea de clústering, veamos la Figura 2.1. Supongamos que tenemos dos características15 para cada individuo (unidad de análisis que se desean agrupar), representadas en los dos ejes de la gráfica y cada punto es una observación o individuo. Por ejemplo, los puntos podrían estar representando clientes y las variables en los ejes ingreso de cada cliente y edad de cada cliente.
Figura 2.1: El problema de la construcción de clústeres
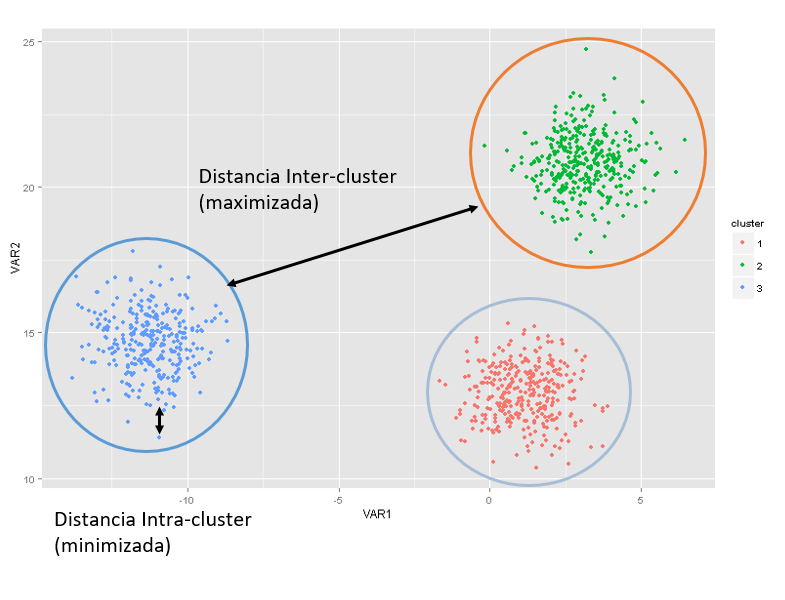
Claramente, podemos ver que hay tres grupos (Ver Figura 2.1) bien separados. La distancia entre los grupos es lo que se llama distancia interclúster y esta distancia es lo que se desea maximizar; por el contrario, la distancia al interior de los clústeres o intraclúster es lo que se quiere minimizar. En esta literatura, la distancia al interior de los grupos se conoce como la coherencia y la distancia entre grupos como separación.
Lo que queremos es tener clústeres relativamente separados entre sí, como se presenta en la Figura 2.1, y al mismo tiempo al interior de los conglomerados los individuos lo más cerca posible (lo más parecidos). Sin embargo, este ideal no se logra siempre. En algunas ocasiones se pueden sobreponer los clústeres.
Dado nuestro objetivo de construir grupos diferentes entre ellos, pero que a la vez sus miembros sean muy similares, cada vez que realicemos la tarea de clústering tendremos que definir tres elementos:
- Una medida de similitud para determinar qué tan “parecidos” (o “qué tan cerca”) son/están los individuos al interior de los grupos y qué tan diferentes son entre grupos. En otras palabras, un criterio para determinar qué significa estar cerca o lejos.
- Un algoritmo para formar los clústeres.
- Un criterio para determinar el número de clústeres.
A continuación, discutiremos cada uno de estos tres elementos.
2.2 Medidas de similitud
Para determinar si los individuos a ser agrupados se encuentran “cercanos” o no, se emplean medidas de similitud. Las medidas de similitud se pueden clasificar en tres grandes grupos:
Grupo de métricas que emplean la distancia, como por ejemplo la distancia euclidiana, Mahalanobis, Manhattan o Minkowski. Este tipo de métricas solo funcionan para variables de intervalo o de razón (variables cuantitativas). Estas medidas se calculan para parejas de observaciones y se resumen en una matriz de distancias.
Grupo de métricas que emplean la correlación. Si se trata de la correlación de Pearson, esta métrica solo funcionan para variables cuantitativas (variables de intervalo o de razón). No obstante, para variables ordinales puede emplearse otro tipo de correlaciones.
Grupo de métricas que emplean coeficientes de asociación. Este tipo de métricas es apropiado solo para variables cualitativas (medidas en escala nominal). En este caso se genera una tabla de comparación y se calculan a partir del Coeficiente de asociación simple, Coeficiente de Jacard, Regrers y Tanimoto, Sorensen o Dice, Sokal y Sneath, o Hannann.
A priori, es difícil determinar cuál tipo de medida de distancia es la más adecuada para cada caso, más allá de descartar algunas medidas por el tipo de variables que se emplean. En últimas, la pregunta de negocio y los datos disponibles y pertinentes para resolver dicha pregunta serán la guía para escoger la medida adecuada de distancia entre las observaciones. Esto implica que, en la práctica, es común que se empleen diferentes medidas de similitud y se comparen los resultados para encontrar cuál medida de similitud (en combinación con el algoritmo de formación de clústeres) genera la agrupación más razonable.
Veamos en detalle la medidas de distancia que se emplean como métrica de similitud.
2.2.1 Medidas de distancia comunes para medir la similitud
Concentrémonos en las medidas de distancia por ser las más empleadas como medidas de similitud. De hecho, no es tan evidente cómo medir la distancia entre dos individuos; en especial si se cuentan con diferentes variables que caracterizan a cada uno de los individuos.
Supongamos que contamos con \(d\) variables (características, features o dimensiones) que se emplearán para realizar el proceso de agrupamiento de \(n\) individuos (observaciones). Definamos a \(x\) como un vector que contiene las \(d\) características (variables que se emplearán en la construcción de los conglomerados) para un individuo. Es decir, \(x= [ x_1 \quad x_2 \quad \cdots \quad x_d ]\). De manera similar \(y\) es un vector que contiene las \(d\) características para otro individuo. En el panel a de la Figura 2.2 se presenta un ejemplo para el caso de dos variables.
La distancia euclidiana entre los dos individuos se define como la distancia al cuadrado entre los dos vectores16. En otras palabras, se calcula la distancia cuadrada entre los dos individuos para cada una de las \(d\) dimensiones, posteriormente se suman esas distancias y finalmente se regresan a la escala original calculando la raíz cuadrada17.
Formalmente,
\[\begin{equation}
d(x,y) = \sqrt{ \left (\sum_{j = 1}^ {d} \left ( x_{j} - y_{j} \right)^ {2} \right)}
\tag{2.1}
\end{equation}\]
En el panel b de la Figura 2.2 se muestra un ejemplo para el caso de dos variables y dos observaciones.
La distancia euclidiana es la medida de distancia más común. Pero tiene un problema, a medida que aumenta la cantidad de variables involucradas en el cálculo de las distancias (dimensionalidad de los datos), la distancia euclidiana resulta menos útil18.
Figura 2.2: Representación de las distancias entre dos observaciones con dos variables
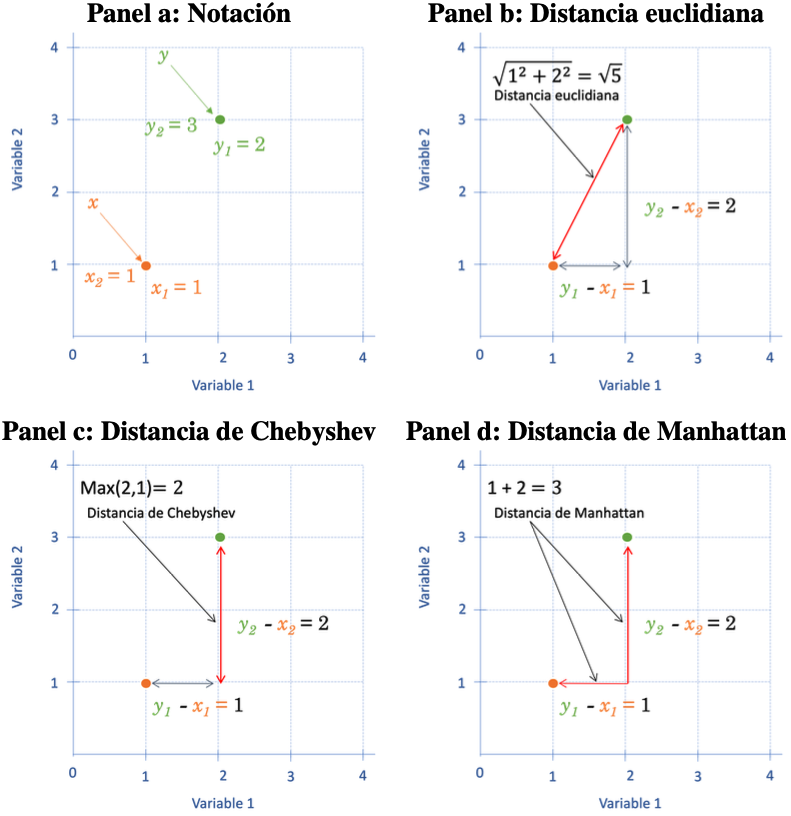
Otro tipo de medida de distancia es la distancia de Chebyshev, Distancia máxima o también conocida como la norma vectorial máxima. La distancia de Chebyshev es la mayor diferencia entre dos vectores a lo largo de cualquier dimensión (variable). En otras palabras, es la distancia máxima entre todas las distancias de cada variable (Ver panel c de la Figura 2.2)19. En este caso: \[\begin{equation} d(x, y) = \max_{1 \leq j \leq d} \left | x_{j} - y_{j} \right | \tag{2.2} \end{equation}\]
Una natural desventaja de esta distancia es que solo tiene en cuenta una dimensión (variable) para medir la proximidad20.
Por otro lado, tenemos la distancia de Manhattan también conocida como la distancia del taxi (en inglés, Taxicab distance) o distancia de la manzana (en inglés City Block distance). Esta distancia toma el nombre de Manhattan porque es la distancia que recorrería un carro en una ciudad (por ejemplo, Manhattan) en la que las manzanas tienen forma de cuadrícula y para ir de un punto a otro en carro solo se puede hacer rodeando las manzanas. Es decir, calcula la distancia entre dos vectores si sólo pudieran moverse en ángulo recto.
Formalmente, esta distancia corresponde a la distancia absoluta entre los dos vectores21. En otras palabras, \[\begin{equation} d(x,y) = \sum_{j = 1}^ {d} \left | x_{j} - y_{j} \right | \tag{2.3} \end{equation}\]
En el panel d de la Figura 2.2 se presenta un ejemplo para dos observaciones y dos variables (dimensiones). La distancia Manhattan funciona relativamente bien para datos con muchas variables (alta dimensión), pero es una medida menos intuitiva que la distancia euclidiana, especialmente cuando se involucran más de dos dimensiones.
Por otro lado, como la distancia de Manhattan utiliza valores absolutos, en lugar de elevar a una potencia o el cálculo de una raíz, esta medida es más robusta frente a valores atípicos. Además, como el módulo es mucho más rápido de calcular que una potencia, esta medida puede ser más rápida en aplicaciones que empleen grandes volúmenes de datos.
La distancia de Canberra es una versión ponderada de la distancia Manhattan22. Esta distancia se define como:
\[\begin{equation} d(x,y) = \sum_{j = 1}^ {d}{ \frac{\left | x_{j} - y_{j} \right |}{\left | x_{j} \right | + \left | y_{j} \right |}} \tag{2.4} \end{equation}\]
Existen otras distancias menos intuitivas como la distancia de Minkowski . Esta distancia es una generalización de las tres primeras distancias estudiadas. Esta es la norma vectorial de orden \(p\). Es decir, la distancia de Minkowski es la \(p\)-ésima raíz de la suma de las \(p\)-ésima potencia de las diferencias de los componentes. En otras palabras,
\[\begin{equation} d(x,y) = \left (\sum_{j = 1}^ {d} \left ( x_{j} - y_{j} \right)^ {p} \right)^{\frac{1}{p}} \tag{2.5} \end{equation}\]
Noten que cuando \(p = 1\), entonces esta distancia es exactamente igual a la de Manhattan. Con \(p = 2\) esta distancia es igual a la euclidiana. Y finalmente, cuando \(p = \infty\) entonces obtendremos la distancia de Chebyshev.
Finalmente, la distancia binaria implica reorganizar los vectores \(x\) y \(y\) como si fueran “bits” binarios. Los elementos que no son cero están “prendidos” (on) y los elementos iguales a cero están “apagados” (off). La distancia es la proporción de bits en los que solo uno está encendido, entre aquellos en los que al menos uno está encendido.
Antes de continuar, es importante anotar que todas estas medidas de distancia son muy sensibles a las unidades en las que se mida cada variable (a la escala). Comúnmente, para evitar este problema, se estandarizan los datos antes de utilizar una medida de distancia. Es decir, se emplean variables centradas (se resta la respectiva media) y con varianza igual (se divide cada una por la respectiva desviación estándar), para evitar que las escalas de medición de las variables y su volatilidad afecten el resultado. A esto lo llamaremos estandarizar los datos23.
2.3 Algoritmos para la formación de clústeres
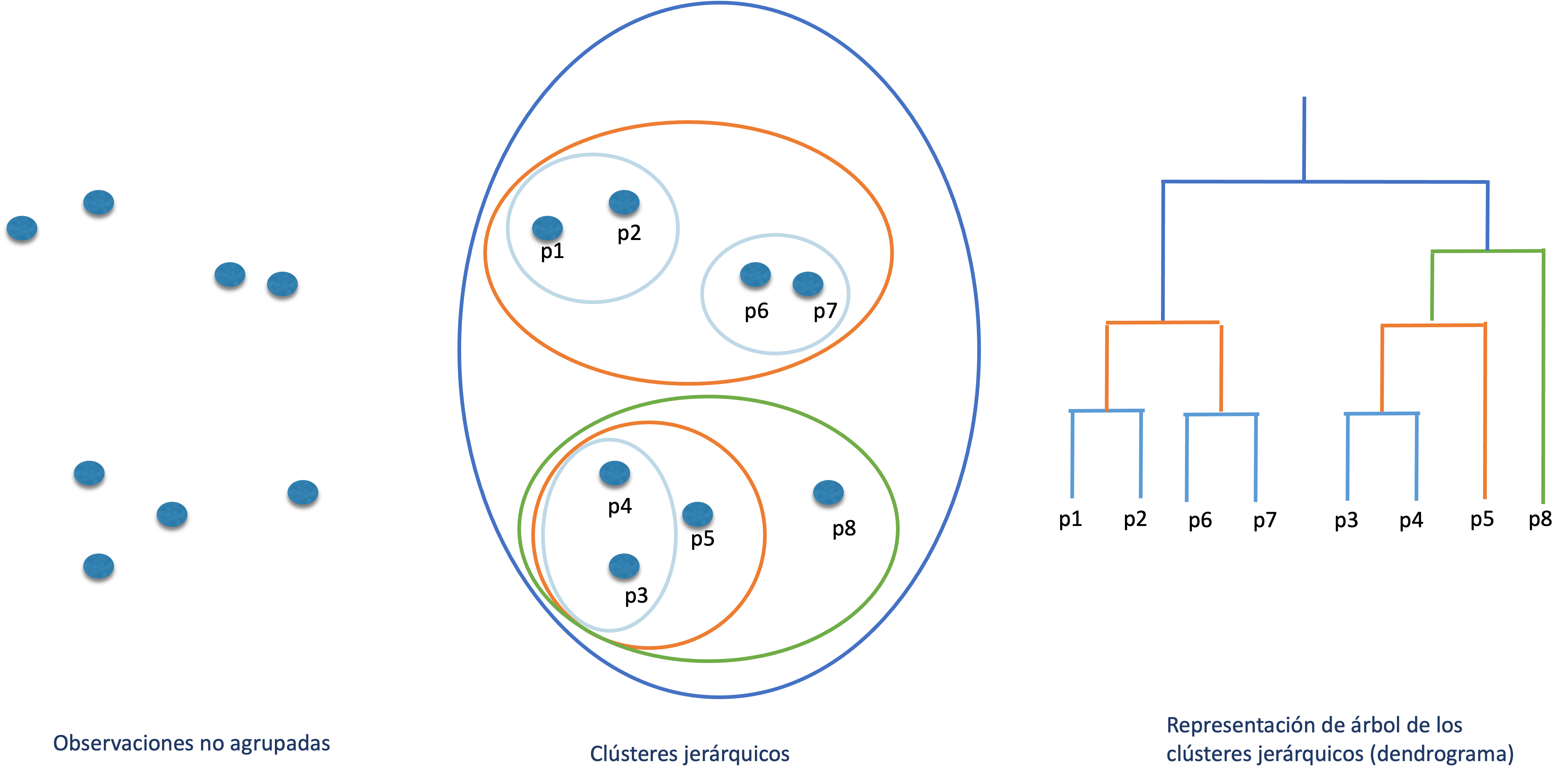
Después de definir la medida de similitud, el segundo elemento necesario para la construcción de los clústeres es seleccionar un algoritmo para la formación de los grupos. Los algoritmos para la formación de clústeres se pueden clasificar en dos tipos: jerárquicos y particionados. Los algoritmos jerárquicos construyen subconjuntos de clústeres organizados jerárquicamente como un árbol (ver Figura 2.3). Estos clústeres por construcción no son mutuamente excluyentes. La intuición de este tipo de de algoritmos se discutirán en el Capítulo 3 y su implementación en R en el Capítulo 4.
Figura 2.3: Clústeres jerárquicos
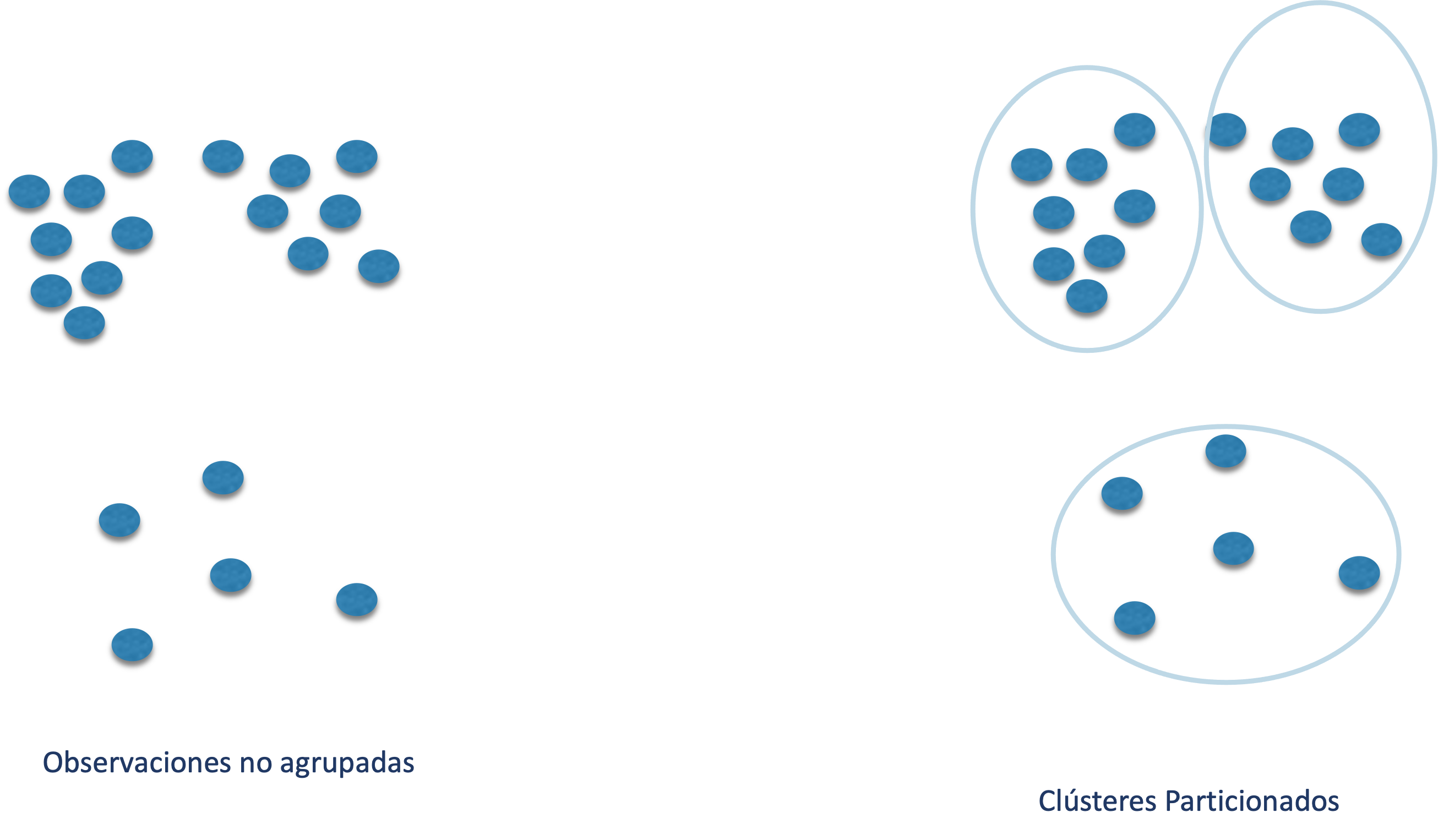
Por otro lado, los algoritmos de clústeres particionados forman grupos que son mutuamente excluyentes; es decir, subconjuntos de individuos que no se sobreponen (ver Figura 2.4). Este tipo de algoritmos los discutiremos en los Capítulos 5 a 9.
Figura 2.4: Clústeres particionados
Los algoritmos de clústering particionados se pueden dividir a su vez en:
- Basados en centroides
- Basados en densidad
- Basados en la distribución
- Métodos que combinan o modifican los anteriores
- Otros tipos de algoritmos de clústering
Los algoritmos basados en centroides establecen un “centro de gravedad” para cada clúster (Ver Figura 2.5). Entre estos modelos tenemos el modelo k-means que divide los datos en \(k\) grupos, donde cada uno tiene un centroide. Los puntos se asignan al grupo con el centroide más cercano. Este algoritmo lo estudiaremos en el Capítulo 5. Otro método similar es k-medoids que emplea medoides (puntos centrales de un cluster) en lugar de centroides (Ver Capítulo 6). El algoritmo k-medoids también es conocido como PAM (por su sigla en inglés del término Partitioning Around Medoids). En esta categoría también se encuentra el modelo CLARA (por su sigla en inglés del término Clustering Large Applications) (Ver Capítulo 6).
Figura 2.5: Clústeres particionados basados en centroides

Una característica de los algoritmos de clústeres particionados basados en centroides es que requieren que el usuario especifique de antemano el número de grupos que se van a crear, mientras que los algoritmos jerárquicos, divide a los individuos en todo los posibles grupos y el científico de datos deberá escoger el número de clústeres. Es decir, estos últimos algoritmos no requieren que se establezca a priori el número de conglomerados.
Por otro lado, los algoritmos basados en densidad convierten áreas de alta densidad de individuos en clústeres. Esto permite grupos de forma arbitraria siempre que se puedan conectar áreas densas. Un ejemplo de estos algoritmos es el DBSCAN (Ver Capítulo 7). El DBSCAN encuentra clústeres basados en la densidad de puntos en el espacio de características (features). No requiere especificar el número de grupos y es bueno para encontrar conglomerados de formas irregulares (Ver Figura 2.6).
Figura 2.6: Clústeres particionados basados en densidad
Los métodos basados en la distribución, también conocidos como basados en modelos, suponen que los datos fueron generados por una distribución de probabilidad determinada. Un ejemplo de estos algoritmos es el Modelo de Mezcla Gausiano (GMM por su sigla en inglés del término Gaussian Mixed Models), que asume que los datos se generan a partir de una mezcla de distribuciones normales. En la Figura 2.7 se muestra una representación del algoritmo GMM que agrupa los individuos, empleando tres distribuciones normales. A medida que aumenta la distancia al centro de la distribución, disminuye la probabilidad de que un punto pertenezca a la distribución. Este modelo lo estudiaremos en el Capítulo 8.
Figura 2.7: Clústeres particionados basados en distribuciones

Adicionalmente, contamos con métodos que combinan o modifican los anteriores como por ejemplo hierarchical K-means y fuzzy clustering (también conocido como FANNY por el término en inglés fuzzy analysis clustering). El modelo FANNY lo estudiaremos en el Capítulo 9.
Finalmente, tenemos otros tipos de algoritmos de clústering para estructuras de datos especiales. Por ejemplo, para datos de redes tenemos los algoritmos de identificación de comunidades. Estos algoritmos encuentran grupos basados en la estructura de la red de conexiones entre los puntos de datos. Otro ejemplo son los algoritmos para hacer clústeres de series de tiempo. Estos algoritmos son útiles para analizar la evolución temporal de muchas variables y encontrar patrones recurrentes. Estos tipos de algoritmos no los estudiaremos.
En este libro nos concentraremos en algoritmos para datos de corte transversal; es decir, muchos individuos, cada uno con diferentes características (variables o features) cuantitativas. Independientemente del método que adoptemos, siempre deberemos responder a la pregunta ¿cuántos clústeres se deberían emplear para agrupar a los individuos? En la siguiente sección discutiremos técnicas para responder esta pregunta.
2.4 Criterio para determinar el número de clústeres
El tercer elemento necesario para la construcción de clústeres es un criterio para determinar el número de grupos razonables. Seleccionar el número de clústeres no es una tarea trivial. El número \(q\) es una variable no observable que reviste cierta dificultad para ser estimada. Es decir, no existe un valor “real” de \(q\) observable que se pueda emplear como referencia.
Por ejemplo, en los modelos de clasificación, regresión y pronósticos se puede guardar una parte de la muestra (muestra de evaluación), para determinar si el modelo que ha sido entrenado (estimado) en la muestra de entrenamiento (de estimación) tiene un buen comportamiento en esta. Es decir, se emplea una muestra de entrenamiento para estimar el modelo. Y posteriormente, los modelos candidatos son comparados en la muestra de evaluación. Entre más “cerca” estén las predicciones del modelo en la muestra de evaluación, mejor será el modelo. Esto siempre será posible con este tipo de modelos que implican un aprendizaje supervisado.
Lastimosamente, en la tarea de clústering esto no es posible. Dado que las observaciones no tienen un rótulo (label) que permita saber con certeza a qué grupo “realmente” pertenece cada individuo, no es posible comparar la “predicción” del grupo con un valor real. Es decir, dada la naturaleza de esta tarea, existe una variable latente (la membresía a un grupo) que queremos “adivinar” pero que no podemos observar para determinar si nos estamos equivocando mucho o poco.
Por eso es necesario tener una aproximación diferente para determinar cuál aproximación es mejor24.
Existen cuatro maneras muy empleadas en la práctica para determinar el mejor número de grupos \(q\): el método del “codo”, el estadístico o índice de Gap (Tibshirani et al., 2001), la silueta promedio o una combinación de un número de métricas. Veamos a continuación cada una de estas aproximaciones.
2.4.1 Selección empleando el método del codo
Este método es tal vez el más conocido y parte de la idea fundamental de las tareas de armar agrupaciones. Recordemos que lo que se busca es encontrar clústeres, de forma que la distancia al interior de los grupos sea la más baja posible. Es decir, que la distancia intraclúster sea la menor posible (Ver Figura 2.1). Una medida de esa distancia intraclúster es la variación total intraclúster (\(WSS\) por su sigla en inglés de Withincluster Sum of Square) que se define como la suma de las distancias de cada una de las observaciones al respectivo centro25 del clúster.
La suma de cuadrados de todas las observaciones que pertenecen a un conglomerado es una medida de la variabilidad de las observaciones dentro de cada clúster. En general, un conglomerado que tiene una suma de cuadrados pequeña es más compacto que uno que tiene una suma de cuadrados grande. Así, la suma (total) de todas estas medidas de variabilidad de los clústeres (\(WSS\)) es una medida de qué tanta variabilidad presentan las observaciones para un determinado número de clústeres \(k\)26.
Entonces, para encontrar el número óptimo de \(k\), se acostumbra graficar en el eje horizontal el número de clústeres y en el eje vertical el \(WSS\) (ver Figura 2.8). El número óptimo de clústeres (\(q\)) corresponderá al valor de \(k\) para el cuál se presente una caída repentina y más grande en el \(WSS\), de tal manera que la gráfica parece tener un “codo” (de ahí el nombre del método).
Figura 2.8: Representación de la selección del número de clústeres óptimo con el método del codo
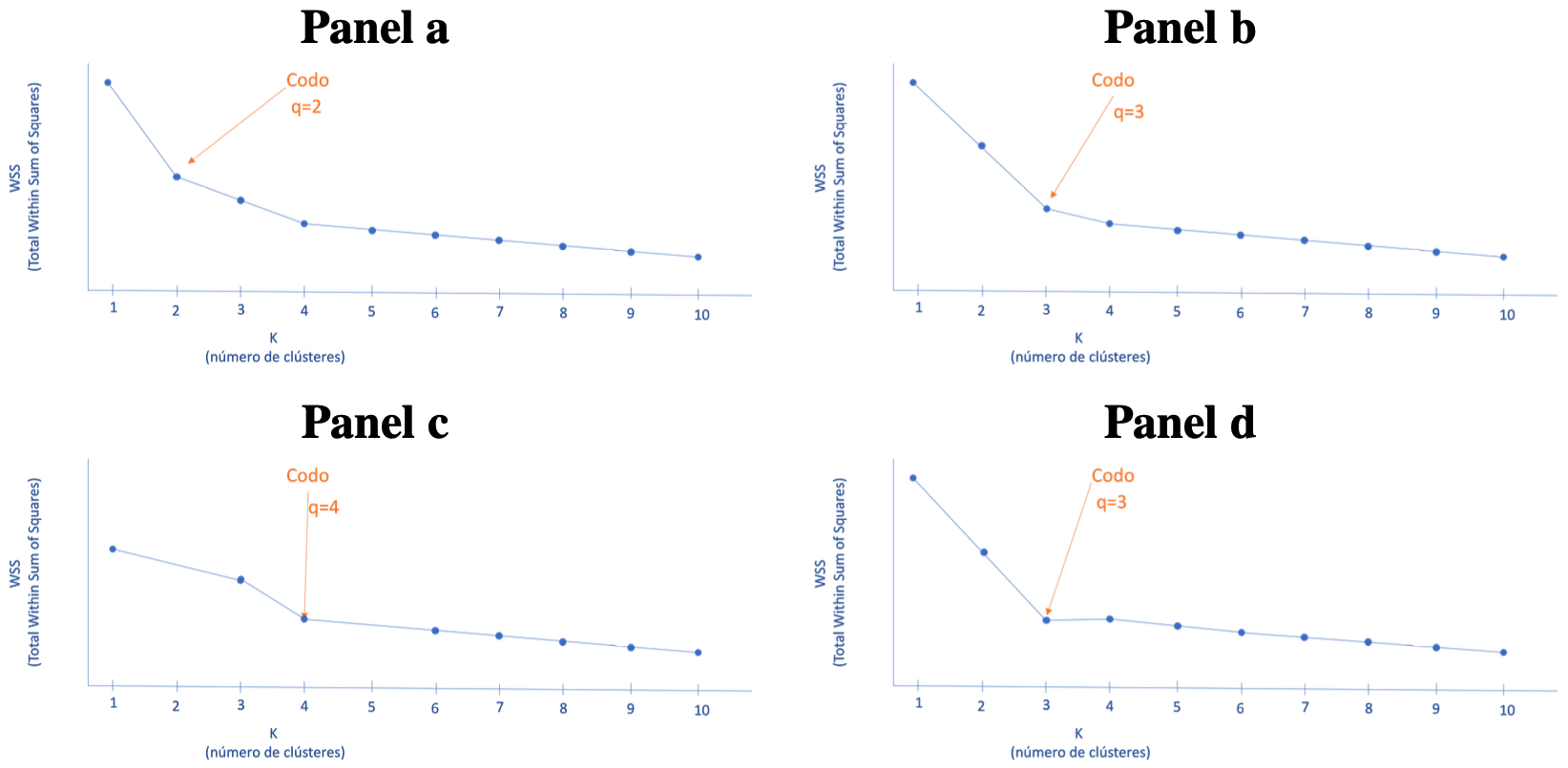
En la Figura 2.8 se presentan diferentes representaciones de la curva \(WSS\) y la selección del número óptimo de clústeres empleando la técnica del codo. Noten que estamos buscando dónde se presente la mayor caída en el \(WSS\) de tal manera que se observa una forma de codo recogido. Por la manera como se selecciona el mejor clúster, este método de selección del número de grupos no permite comparar entre diferentes algoritmos de formación de clústeres.
2.4.2 Selección empleando el estadístico de Gap
Otra manera muy empleada para seleccionar el número óptimo de clústeres es el estadístico Gap27 propuesto por Tibshirani et al. (2001).
El estadístico de la brecha compara la variación total dentro del clúster (\(WSS\)) para diferentes valores de \(k\) con sus valores esperados bajo la distribución uniforme de referencia. Esto permite encontrar para cada \(k\) qué tanto se aleja el \(WSS\) del valor esperado, cuando todos los datos se distribuyen de manera aleatoria (y uniforme). En la Sección 2.4.2 se presenta el cálculo de este estadístico.
Intuitivamente, el número de grupos óptimo (\(q\)) será aquel para el cual la estructura de agrupación se aleja más de la distribución uniforme aleatoria de los puntos. Tibshirani et al. (2001) demuestran que esto ocurre cuando el número de clústeres corresponde al menor de los valores \(k\) para el que el estadístico Gap se aleja menos de una desviación estándar del valor Gap del siguiente (\(k+1\)). Afortunadamente, R hará ese cálculo por nosotros. Por la manera cómo se selecciona el mejor clúster, este método de selección del número de conglomerados no permite comparar entre diferentes algoritmos de formación de clústeres.
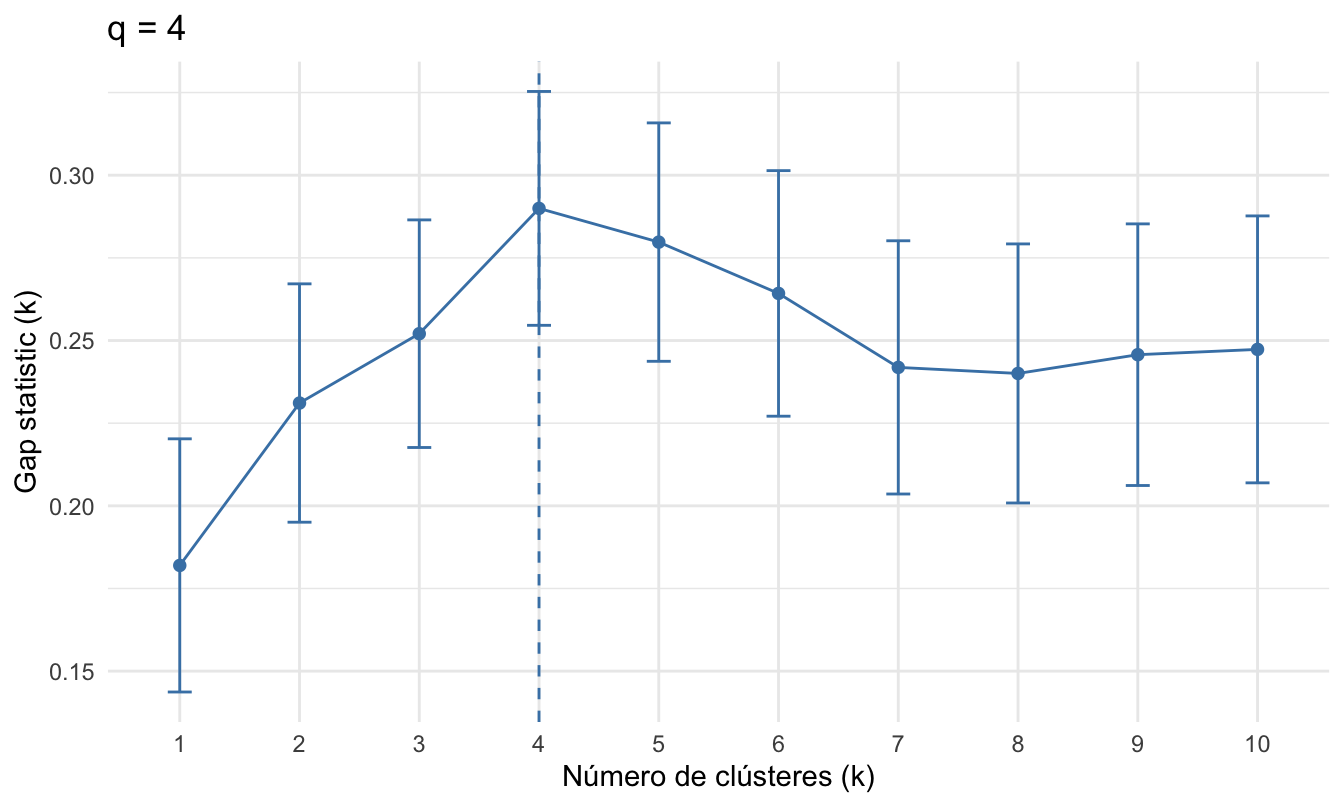
Al igual que con el método del codo, es común que este estadístico se calcule para un número de \(k\) y se grafique incluyendo el respectivo intervalo de confianza. Y R presentará con una línea punteada el \(k\) que garantiza la condición establecida por Tibshirani et al. (2001). La Figura 2.9 presenta un ejemplo en el que el número óptimo de conglomerados es 4.
Figura 2.9: Ejemplo de la selección del número de clústeres óptimo empleando el estadístico GAP
2.4.3 Selección empleando la silueta promedio
La silueta es una medida de qué tan similar es un objeto a su propio grupo (cohesión) en comparación con otros grupos (separación). Empecemos por definir un individuo \(i\) que pertenece al clúster \(C\) como \(C_i\). Entonces, una medida para el individuo \(i\) de su cohesión con el grupo \(C_i\) es:
\[\begin{equation} a(i) = \frac{1}{|C_i| - 1} \sum_{j \in C_i, i \neq j} d(i, j) \tag{2.6} \end{equation}\]
donde \(d(i, j)\) es la distancia28 entre el individuo \(i\) y el \(j\) que también pertenece al clúster \(C_i\). Es decir, \(a(i)\) representa la distancia promedio del individuo \(i\) a todos los otros puntos del clúster \(C_i\). Por eso también es conocida como la distancia promedio intraclúster.
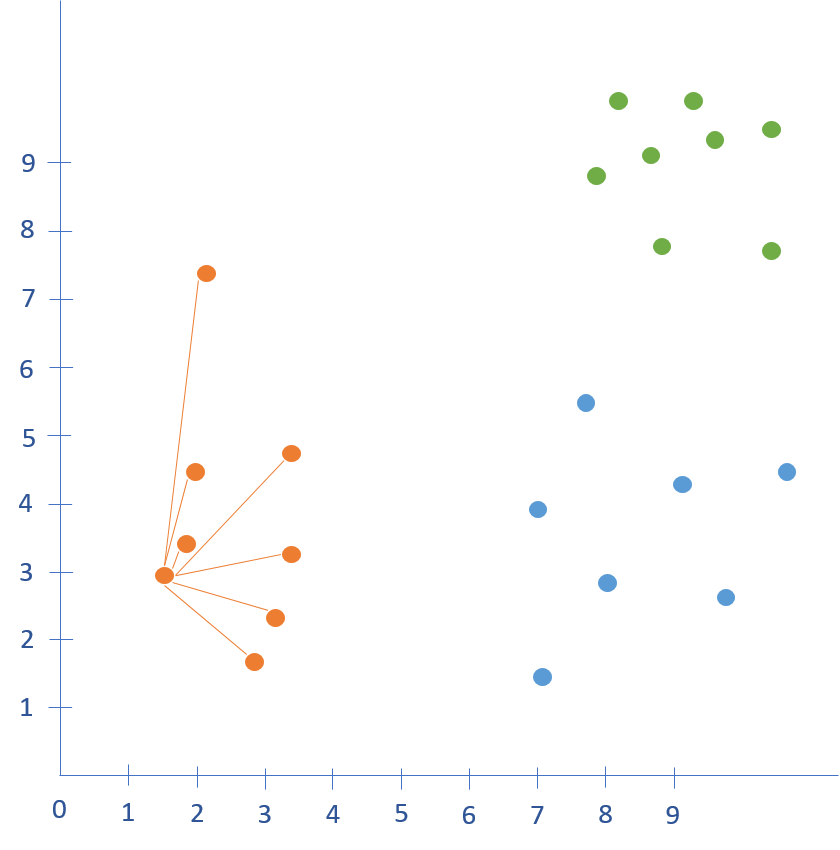
La Figura 2.10 muestra una representación de todas las distancias (en rojo) a las que se le sacaría el promedio para calcular \(a(i)\) para el individuo seleccionado. Entonces, \(a(i)\) se puede interpretar como una medida de la asignación de \(i\) al clúster \(C_i\). Entre más pequeño sea \(a(i)\) mejor es la cohesión; i.e. mejor fue la decisión de asignar el individuo \(i\) al clúster \(C_i\).
Figura 2.10: Representación de la distancia intraclúster para un individuo \(i\)
Ahora podemos medir qué tan diferente es el individuo \(i\) de todas las observaciones de otro clúster (por ejemplo el clúster \(C_k\)) como \[\begin{equation} \frac{1}{|C_k|} \sum_{j \in C_k} d(i, j) \tag{2.7} \end{equation}\] para todo \(k \neq i\). Esta distancia también se conoce como la distancia interclúster para el individuo \(i\). Noten que existirán tantas distancias interclústeres como números de conglomerados menos uno (\(q-1\)) para cada observación29. Supongamos que contamos con tres clústeres: los naranjas, los azules y los verdes. Entonces existirán dos distancias interclúster para una observación del clúster naranja, como se puede observar en la Figura 2.11. Noten que todas las líneas azules se promediarán, así como todas las verdes para producir dos distancias (promedio) interclúster.
Figura 2.11: Representación de la distancia interclúster para un individuo \(i\)
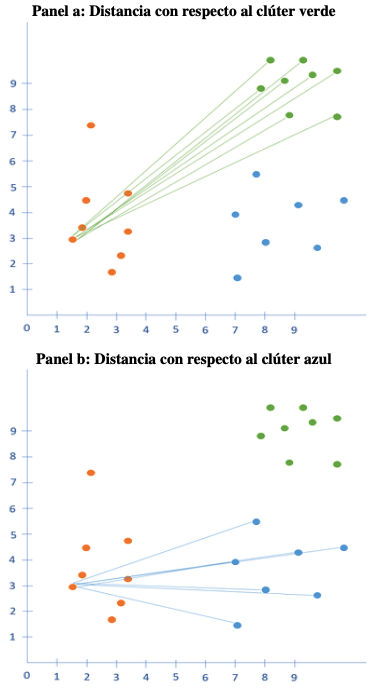
Ahora calculemos para cada individuo \(i\) del clúster \(C_i\) el clúster más cercano (el vecino más cercano) de la siguiente manera: \[\begin{equation} b(i) = \min_{k \neq i} \frac{1}{|C_k|} \sum_{j \in C_k} d(i, j) \tag{2.8} \end{equation}\] Es decir, \(b(i)\) es una medida de qué tan cerca se encuentra el clúster más cercano (diferente al que ya pertenecía (\(C_i\))).
La silueta para una observación determinada \(i\) es una combinación de la cohesión \(a(i)\) y \(b(i)\). La silueta para el individuo \(i\) está definida como:
\[\begin{equation} s(i) = \frac{b(i) - a(i)}{\max\{a(i),b(i)\}} \tag{2.9} \end{equation}\] Esto es equivalente a \[\begin{equation} s(i) = \left\{\begin{matrix} 1-a(i)/b(i)& si & a(i)<b(i)\\ 0 & si & a(i) = b(i) \\ b(i)/a(i)-1 & si & a(i)>b(i) \\ \end{matrix}\right. \tag{2.10} \end{equation}\] Esta idea fue propuesta por Rousseeuw (1987).
Es fácil demostrar que \(s(i)\) se encuentra entre -1 y +1. Entre más cercano a uno indica que el individuo \(i\) está bien ubicado en su conglomerado. Es decir, la clasificación actual en \(C_i\) es mejor que con los grupos vecinos. Por otro lado, un valor cerca a cero o negativo implica que es posible que el individuo fue mal clasificado en su clúster \(C_i\).
Si la mayoría de individuos tienen un valor alto de \(s(i)\), entonces la estructura de agrupamiento es apropiada. Si muchos individuos tienen una silueta baja o negativa, entonces la estructura encontrada con los clústeres puede tener demasiados o muy pocos clústeres. Dado que en un ejercicio de clústering nos podemos contar con muchos individuos, es común que se calcule la silueta promedio para cada clúster y para todos los individuos.
En general una regla empírica comúnmente aceptada es :
- Si la silueta (promedio o individual) está entre 0.71 y 1.0 entonces la estructura de clasificación encontrada es fuerte.
- Si la silueta (promedio o individual) está entre 0.51 y 0.7 entonces la estructura de clasificación encontrada es razonable (aceptable).
- Si la silueta (promedio o individual) está entre 0.26 y 0.50 entonces la estructura de clasificación encontrada es débil y puede ser artificial.
- Si la silueta (promedio o individual) es < 0.25 entonces no se ha encontrado una estructura de clasificación.
En la práctica, se emplea la silueta promedio para escoger el número óptimo de grupos. De igual manera que en el método del codo y el estadístico del Gap, la silueta promedio es calculada para un número relativamente grande de clústeres (\(k\)) y se selecciona el número óptimo de conglomerados (\(q\)) donde la silueta promedio es maximizada. Por otro lado, también es común emplear las siluetas individuales para ver cuáles observaciones quedan mejor asignadas a un clúster. Finalmente, es importante aclarar que la silueta promedio permite comparar diferentes algoritmos para formar clústeres.
2.4.4 Selección empleando batería de métricas
En la literatura se han desarrollado una gran variedad de índices de validación que permitan comparar diferentes aproximaciones. Estos índices o métricas combinan de diferente manera información sobre la compacidad de la aproximación30 de generar grupos parecidos (intragrupo) y grupos muy diferentes (el aislamiento entre grupos o intergrupos). En el Anexo de este Capítulo (Ver Sección 2.6) se presentan 30 métricas diferentes que comúnmente se emplean.
En la práctica, estos 30 índices se calculan para un número relativamente grande de posibles aproximaciones para determinar el algoritmo de construcción, medida de distancia y número de clústeres. El número de clústeres que sea seleccionado por la mayor cantidad de estos índices es considerado el mejor número de clústeres \(q\). En los siguientes capítulos veremos ejemplos de esto.
2.5 Comentarios finales
Hasta el momento hemos discutido las generalidades de la tarea de clústering. Vimos que la construcción de clústeres implica seleccionar tanto un algoritmo, una métrica de distancia y una manera de seleccionar el número de clústeres. En los siguientes capítulos veremos diferentes algoritmos de construcción de clústering. Para seleccionar el número de clústeres (\(q\)) emplearemos los métodos discutidos en este capítulo.
2.6 Anexo: Índices de validación
Para describir cada uno de los 30 índices de validación más usados, empleemos, siguiendo a Charrad et al. (2014), la siguiente notación:
- \(n\): Número de observaciones.
- \(d\): Número de variables o características.
- \(q\): Número de clústeres.
- \(X\): Matriz de datos con \(n\) filas y \(d\) columnas (cada columna corresponde a una variable. Es decir, \(x_{ij}\), \(i\) = 1,2,…, \(n\) y \(j\)= 1,2,…,\(p\).
- \(\overline{X}\): Matriz \(q\) x \(d\) de métodos de agrupación (clúster).
- \(\overline{x}\): Matriz centroide X.
- \(n_k\): Número de objetos en el clúster \(C_k\).
- \(c_k\): Centroide del clúster \(C_k\).
- \(x_i\): Vector de \(d\) dimensiones de observaciones del \(i\)-ésimo objeto en el clúster \(C_k\). En algunas ocasiones, para simplificar la notación se eliminará el subíndice.
- \(\left \| x \right \|\): Corresponde a \((x^Tx)^{1/2}\) (en este caso se omitieron los subíndices).
- \(W_q\): Se define como \(\sum_{k=1}^{q}\sum_{i \in C_k}(x_i-c_k)(x_i-c_k)^T\) Es la matriz de dispersión intraclúster, clusterizada en \(q\) clústeres.
- \(B_q\): Se define como \(\sum_{k=1}^{q}n_k(c_k-\overline{x})(c_k-\overline{x})^T\): Es la matriz de dispersión interclúster, agrupada en \(q\) clústeres.
- \(N_t\): Número total de pares de observaciones en los datos: \(N_t = \frac{n(n-1)}{2}\).
- \(N_w\): Número de pares de observaciones que pertenecen al mismo clúster: \(N_w = \sum_{k=1}^{q} \frac{n_k(n_k-1)}{2}\)
- \(N_b\): Número de pares de observaciones que pertenecen a diferentes clústeres. Es decir, \(N_b = N_t-N_w\).
- \(S_w\): Suma de las distancias intraclúster. Es decir, \(S_w = \sum_{q}^{k=1}\sum_{i,j \in C_k} d(x_i,x_j)\).
- \(S_b\): Suma de las distancias interclúster. Es decir,\(S_b = \sum_{q-1}^{k=1}\sum_{l=k+1}^{q} \sum_{i \in C_k}d(x_i,x_j)\).
A continuación, se describen las 30 métricas más empleadas para la selección de \(q\).
2.6.1 Índice CH
El índice de Calinski y Harabasz (CH) (Caliński & Harabasz, 1974) está definido como:
\[\begin{equation} CH(q) = \frac{tr(B_q)/(q-1)}{tr(W_q)/(n-q)} \tag{2.11} \end{equation}\]
donde \(tr\) representa la traza de una matriz. El valor de \(q\) que maximiza la función \(CH(q)\) sería el número de clústeres seleccionado con este método.
2.6.2 Índice Duda
Duda et al. (1973) propusieron un criterio usando la siguiente razón:
\[\begin{equation} Je(2)/Je(1) \tag{2.12} \end{equation}\]
donde \(Je(2)\) es la suma de las distancias al cuadrado intraclúster cuando los datos están divididos en dos clústeres, y \(Je(1)\) es la distancia intraclúster al cuadrado con un solo clúster. Este índice se define como:
\[\begin{equation} Duda = \frac{Je(2)}{Je(1)}=\frac{W_k+W_l}{W_m} \tag{2.13} \end{equation}\]
Se asume que los clústeres \(C_k\) y \(C_l\) se unen para formar \(C_m\). Según Gordon (1999), el número óptimo de clústeres es el \(q\) más pequeño, tal que:
\[\begin{equation} Duda \geq 1- \frac{2}{\pi d}-z\sqrt{\frac{2(1-\frac{8}{\pi^2d})}{n_md}}=\mathit{Valor \ crítico \ Duda} \tag{2.14} \end{equation}\]
2.6.3 Índice Pseudo \(t^2\)
Duda et al. (1973) propusieron otro índice denominado el Pseudo \(t^2\), el cual solo es aplicable a métodos jerárquicos:
\[\begin{equation} \mathit{Pseudo \ } t^2 = \frac{V_{kl}}{\frac{W_k+W_l}{n_k+n_l-2}} \tag{2.15} \end{equation}\] donde \(V_{kl}\)=\(W_{m}\)-\(W_{k}\)-\(Wl\), si \(C_m=C_k \cup C_l\).
Gordon (1999) demostró que el número óptimo de clústeres es el mejor \(q\) tal que:
\[\begin{equation} \mathit{Pseudo \ } t^2 \leq \frac{1-\mathit{Valor \ crítico \ Duda}}{\mathit{Valor \ crítico \ Duda}}\cdot(n_k+n_l-2) \tag{2.16} \end{equation}\]
2.6.4 Índice C
El índice C fue propuesto por L. J. Hubert & Levin (1976). Se calcula como:
\[\begin{equation} \mathit{Indice \ C} = \frac{S_w-S_{min}}{S_{max}-S_{min}}, S_{min} \neq S_{max}, \mathit{Indice \ C} \in (0,1) \tag{2.17} \end{equation}\]
donde
- \(S_{min}\): Es la suma de las \(N_w\) pequeñas distancias entre todos los pares de puntos de los datos (\(N_t\) es el número de pares).
- \(S_{max}\): Es la suma de las \(N_w\) mayores distancias entre todos los pares de puntos de los datos totales.
Milligan & Cooper (1985) y Gordon (1999) sugieren que el número óptimo de clústeres se fije encontrando el número de clústeres (\(Q\)) para el cual este índice se minimiza.
2.6.5 Índice Gamma
El Índice Gamma es una adaptación del estadístico Gamma de Goodman y Kriskal para usar en clústeres (Baker & Hubert, 1976).
Se hacen comparaciones entre las diferencias de los individuos del mismo clúster (intraclúster) y entre los individuos de diferentes clústeres (interclúster) . Una comparación es concordante (discordante) si la diferencia intraclúster es estrictamente menor (estrictamente mayor) a la diferencia interclúster. Las igualdades entre un par de grupos diferentes son ignoradas en definición del índice (Gordon, 1999). El índice se define como:
\[\begin{equation} Gamma=\frac{s(+)-s(-)}{s(+)+s(-)} \tag{2.18} \end{equation}\]
donde
- \(s(+)\): Es el número de comparaciones concordantes.
- \(s(-)\): Es el número de comparaciones discordantes.
El máximo valor del índice representa el número correcto de clústeres (Milligan & Cooper, 1985).
2.6.6 Índice de Beale
Beale (1969) propuso un estadístico F para probar la hipótesis de la existencia de \(q_1\) contra \(q_2\) clústeres en los datos, donde \(q_2 > q_1\).
\[\begin{equation} Beale_F \equiv \frac{\frac{V_{kl}}{W_k + W_l}}{(\frac{n_m -1}{n_m -2})2^{\frac{2}{d}}-1} \tag{2.19} \end{equation}\]
donde \(V_{kl}\) = \(W_m\)-\(W_k\)-\(W_l\). Se asume que los clústeres \(C_k\) y \(C_l\) se unen para formar \(C_m\). El número óptimo de clústeres se obtiene comparando \(F\) con una distribución \(F_{d,(n_m-2)d}\). Para valores significativamente grandes de \(F\), la hipótesis nula de un solo clúster es rechazada (Gordon, 1999).
2.6.7 Índice CCC
El Criterio Cúbico de Clústering (Cubic Clustering Criterion - CCC en inglés) es una prueba estadística, cuyo estadístico de prueba está dado por:
\[\begin{equation} CCC=\ln{\left[\frac{1-E(R^2)}{1-R^2}\right]}\frac{\sqrt{\frac{nd^*}{2}}}{(0.001+E(R^2))^1.2} \tag{2.20} \end{equation}\]
donde \[ R^2=1-\frac{tr(X^TX-\overline{X}^TZ^TZ\overline{X})}{tr(X^TX)} \]
\(\overline{X}\) corresponde al producto \((Z^TZ)^{-1}Z^TX\), donde \(Z\) es una matriz indicadora de clústeres (\(n x q\)) con \(z_{ik}\) = 1 si la observación \(i\) pertenece al clúster \(k\) y \(z_{ik}\)= 0 de lo contrario. Adicionalmente, \[ E(R^2)=1-\left[\frac{\sum_{j=1}^{d*}\frac{1}{n+u_j}+\sum_{j=d*+1}^p\frac{u^2_j}{n+u_j}}{\sum_{j=1}^d}\right]\left[\frac{(n-d)^2}{n}\right]\left[1+\frac{4}{n}\right] \] donde \(u_j\) es \(\frac{s_j}{c}\) y \(s_j\) es la raíz cuadrada del valor propio \(j\) de \(\frac{X^TX}{(n-1)}\). Y \(c=\left(\frac{v*}{q}\right)^{\frac{1}{d*}}\). Además, \(v*= \Pi^{d*}_{j=1}s_j\) y \(d*\) es el mayor entero escogido menor que \(q\) tal que \(u_{d*}\) no es menor que 1.
El máximo valor del índice indica el número óptimo de clústeres en los datos (Milligan & Cooper, 1985).
2.6.8 Índice Pt-biserial
Este índice, propuesto por Milligan (1980) y Kraemer (2004), es una correlación bi-serial entre la matriz de entrada de diferencias y una matriz correspondiente con entradas 0 y 1; 0 es asignado si los dos puntos correspondientes están clusterizados juntos por el algoritmo, y 1 es lo contrario (Milligan, 1980).
Dado que los valores positivos más grandes reflejan un mejor ajuste entre los datos y la división encontrada, el máximo valor del índice es usado para seleccionar el número óptimo de clústeres (Milligan, 1980).
El coeficiente de correlación bi-serial se calcula de la siguiente manera (Milligan, 1981).
\[\begin{equation} Ptbiserial = \frac{[\overline{S}_b-\overline{S}_w][N_wN_b/N_t^2]^{1/2}}{s_d} \tag{2.21} \end{equation}\]
donde \(\overline{S}_w\): \(S_w/N_w\), \(\overline{S}_b\): \(S_b/Nb\) y \(s_d\) es la desviación estándar de todas las distancias.
2.6.9 Índice Gplus
Este índice fue diseñado por Rohlf (1974) y reformulado por Milligan (1981). Se calcula de la siguiente manera:
\[\begin{equation} Gplus=\frac{2s(-)}{N_t(N_t-1)} \tag{2.22} \end{equation}\]
donde \(s(-)\) es el número de comparaciones discordantes o el número de veces que dos puntos que estaban en el mismo clúster tenían una distancia mayor que dos puntos, que no se clusterizaron juntos (Milligan, 1981). Los valores mínimos del índice determinan el número óptimo de clústeres (Milligan & Cooper, 1985).
2.6.10 Índice DB
El índice de Davies & Bouldin (1979) es una función de la suma de ratios intraclúster dispersos a separación interclúster. Este índice se define como:
\[\begin{equation} DB(q)=\frac{1}{q}\sum_{k=1}^q\max_{k\neq l}\left(\frac{\delta_k+\delta_l}{D_{kl}}\right) \tag{2.23} \end{equation}\]
donde \(k, l = 1,...,q\) es el número de clústeres. \(D_{kl}=\sqrt[v]{\sum_{j=1}^d |c_{kj}-c_{lj}|}^v\) es la distancia de Minkowski entre los centroides de los clústeres \(C_k\) y \(C_l\). \(\delta_k\) es una medida de dispersión de un clúster \(C_k\) con respecto al centroide de ese clúster empleando la distancia Minkowski.
Según Milligan & Cooper (1985) y Davies & Bouldin (1979), el valor de \(q\) que minimiza DB(\(q\)) corresponde al número de clústeres óptimo.
2.6.11 Índice de Frey
El índice propuesto por Frey & Van Groenewoud (1972) solo puede ser aplicado a métodos jerárquicos. Es el ratio de la diferencia entre puntajes de dos niveles sucesivos en la jerarquía. El numerador es la diferencia entre la media de distancias interclúster, \(\overline{D}_b\), de cada uno de los dos niveles jerárquicos (nivel \(j\) y \(j +1\)). Los autores proponen usar un puntaje (ratio) de 1.00, para identificar el nivel correcto del clúster. Los ratios suelen ser mayores o menores de 1.
Los mejores resultados se dieron cuando se continuó la clusterización hasta que el último ratio fue menor de 1.00. En este punto, el nivel del clúster anterior era tomado como partición óptima. Si el ratio nunca era menor de 1, se asumía que la solución era un solo clúster (Milligan & Cooper, 1985). Este indicador se define como:
\[\begin{equation} Frey=\frac{\overline{S}_{b,j+1}-\overline{S}_{b,j}}{\overline{S}_{w,j+1}-\overline{S}_{w,j}} \tag{2.24} \end{equation}\]
donde \(\overline{S}_b\)=\(S_b/N_b\) es la media de la distancia interclúster y \(\overline{S}_w\)=\(S_w/N_w\) es la media de la distancia intraclúster.
2.6.12 Índice de Hartigan
Este índice se calcula de la siguiente manera (Hartigan, 1975):
\[\begin{equation} Hartigan=\left(\frac{tr(W_q)}{tr(W_{q+1})}-1\right)(n-q-1) \tag{2.25} \end{equation}\]
donde \(q \in \left\{1,...,n-2 \right\}\). La máxima diferencia entre niveles jerárquicos es el indicativo del número correcto de clústeres (Milligan & Cooper, 1985).
2.6.13 Índice Tau
Este índice, propuesto por Rohlf (1974) y revisado por Milligan (1981), se calcula entre las entradas correspondientes de dos matrices. La primera contiene las distancias entre los objetos y la segunda es una matriz de 0 y 1 que indica si un par de puntos están dentro del mismo clúster o no.
\[\begin{equation} Tau=\frac{s(+)-s(-)}{[(N_t(N_t-1)/2-t)(N_t(N_t-1)/2)]^{1/2}} \tag{2.26} \end{equation}\]
El máximo valor del índice es tomado como indicativo del número correcto de clústeres (Milligan & Cooper, 1985).
2.6.14 Índice de Ratkowsky
Ratkowsky & Lance (1978) propusieron un criterio para determinar el número óptimo de clústeres basados en \(\frac{\overline{S}}{q^{1/2}}\). El valor de \(\overline{S}\) es el promedio de los ratios de (\(\frac{BGSS_J}{TSS_j}\)), donde \(BGSS\) es la suma de cuadrados interclúster para cada variable31 y \(TSS\) es el total de la suma de cuadrados para cada variable32 (Hill, 1980).
El número óptimo de clústeres es el valor \(q\) para el cual \(\frac{\overline{S}}{q^{1/2}}\) alcanza su valor máximo (Milligan & Cooper, 1985). Si el valor de \(q\) se hace constante, este criterio se ve reducido de \(\frac{\overline{S}}{q^{1/2}}\) a \(\overline{S}\) (Hill, 1980).
\[\begin{equation} Ratkowsky=\frac{\overline{S}}{q^{1/2}} \tag{2.27} \end{equation}\]
donde \(\overline{S}^2=\frac{1}{d} \sum_{j=1}^d \frac{BGSS_j}{TSS_j}\).
2.6.15 Índice de Scott
Scott & Symons (1971) introdujeron un índice basado en la siguiente ecuación:
\[\begin{equation} Scott = n \log\left ( \frac{det(T)}{det(S_q)} \right ) \tag{2.28} \end{equation}\]
donde \(n\) es el número de elementos en los datos, \(T\) es la suma total de cuadrados y \(S_q\) es la suma de cuadrados entre los \(q\) clústeres.
La máxima diferencia entre los niveles jerárquicos se usa para sugerir el número correcto de particiones (Milligan & Cooper, 1985).
2.6.16 Índice de Marriott
Marriott (1971) propuso el siguiente índice:
\[\begin{equation} Marriot = q^2 det(S_q) \tag{2.29} \end{equation}\]
La máxima diferencia entre niveles sucesivos se usa para determinar el mejor nivel de partición (Milligan & Cooper, 1985).
2.6.17 Índice de Ball
Ball & Hall (1965) propusieron un índice basado en la distancia promedio entre los objetos y su respectivo centroide del clúster. Se calcula:
\[\begin{equation} Ball = \frac{S_q}{q} \tag{2.30} \end{equation}\]
La diferencia más grande entre niveles se usa para indicar la solución óptima (Milligan & Cooper, 1985). (Ver también Dimitriadou et al. (2002)).
2.6.18 Índice de Trcovw
Este índice, propuesto por Milligan & Cooper (1985), recoge la información en la matriz de covarianzas intraclústeres por medio de la traza (Ver también Dimitriadou et al. (2002)). Es decir,
\[\begin{equation} Trcovw=tr(Cov(W_q)) \tag{2.31} \end{equation}\]
La máxima diferencia entre los puntajes de los niveles es usada para indicar la solución óptima (Milligan & Cooper, 1985).
2.6.19 Índice de Tracew
Este índice ha sido una de las sugerencias más populares en la literatura, por ejemplo ha sido propuesto por Milligan & Cooper (1985), Edwards & Cavalli-Sforza (1965), Friedman & Rubin (1967), Orlóci (1967) y Fukunaga & Koontz (1970). No emplea la covarianza de la matriz de distancias intraclústeres, sino la misma matriz de distancias. En otras palabras,
\[\begin{equation} Tracew=tr(W_q) \tag{2.32} \end{equation}\]
Dado que este criterio aumenta monótonamente con soluciones que contienen menos clústeres, el máximo de las segundas diferencias de los puntajes es usado para determinar el número de clústeres en los datos (Milligan & Cooper, 1985).
2.6.20 Índice de Friedmdan
Este índice fue propuesto por Friedman & Rubin (1967) como una métrica para un método de clústering no jerárquico (para una mayor discusión ver Dimitriadou et al. (2002)). Formalmente, se define cómo: \[\begin{equation} Friedman=tr(W_{q}^{-1}B_q) \tag{2.33} \end{equation}\]
La diferencia máxima entre los valores de este criterio es usada para indicar el número óptimo de clústeres (Milligan & Cooper, 1985).
2.6.21 Índice de McClain
El índice de McClain y Rao (McClain & Rao, 1975) consiste en el ratio de entre el promedio de distancias intraclúster y el número de distancias intraclúster dividido por el número de distancias. Es decir, \[\begin{equation} \mathit{McClain}=\frac{\overline{S}_w}{\overline{S}_b} = \frac{S_w/N_w}{S_b/N_b} \tag{2.34} \end{equation}\]
El valor mínimo del índice es usado para indicar el número óptimo de clústeres.
2.6.22 Índice de Rubin
Friedman & Rubin (1967) propusieron otro criterio basado en el ratio del determinante de la matriz de la suma total de cuadrados y productos cruzados con el determinante de los agrupados en la matriz de conglomerados. Formalmente: \[\begin{equation} Rubin= \frac{det(T)}{det(W_q)} \tag{2.35} \end{equation}\]
Milligan & Cooper (1985) y Dimitriadou et al. (2002) sugieren emplear el valor mínimo de las segundas diferencias entre niveles para seleccionar el número óptimo de clústeres.
2.6.23 Índice de KL
Propuesto por Ratkowsky & Lance (1978), este índice se define como: \[\begin{equation} KL(q)=\left | \frac{DIFF_q}{DIFF_{q+1}} \right | \tag{2.36} \end{equation}\] donde \(DIFF_q=(q-1)^{\frac{2}{p}}tr(W_{q-1})-q^{\frac{2}{p}}tr(W_q)\). El valor de \(q\) que maximiza \(KL(q)\) sugiere el número óptimo de clústeres.
2.6.24 Índice de Silueta
En la Sección 2.4.3 discutimos la silueta promedio propuesta por Rousseeuw (1987). Éste se emplea como un índice más para comparar las diferentes aproximaciones. El valor máximo del índice es usado para determinar el número óptimo de clústeres (Kaufman & Rousseeuw, 2009).
2.6.25 Índice de Gap
El estadístico Gap fue propuesto por Tibshirani et al. (2001) y se calcula de la siguiente forma: \[\begin{equation} Gap(q)=\frac{1}{B}\sum_{b=1}^{B}{log\left ( W_{qb} \right )-log\left ( W_q \right )} \tag{2.37} \end{equation}\]
donde \(W_{qb}\) es la matriz intraclúster definida como en el índice de Hartigan . El número óptimo de clústeres se elige encontrando el menor \(q\) tal que:
\[\begin{equation} Gap(q)\geq Gap(q+1)-s_{q+1} \tag{2.38} \end{equation}\] para \(q=1,...,n-2\).
2.6.26 Índice D
El índice D (Lebart et al., 1995) está basado en la ganancia del clúster de la inercia intraclúster. La inercia intraclúster mide el grado de homogeneidad entre los datos asociados con un clúster. Calcula las distancias comparadas con el punto de referencia que representa el perfil del clúster (centroide). Se define como: \[\begin{equation} w(P^q)=\frac{1}{q}\sum_{k=1}^{q}{\frac{1}{n_k}\sum_{x_i\epsilon C_k}{d(x_i,c_k)}} \tag{2.39} \end{equation}\]
Dadas dos particiones, \(P^{k-1}\) compuesta por \(k-1\) clústeres y \(P^k\) compuesta por \(k\) clústeres, la ganancia del clúster de la inercia intraclúster se define como: \[\begin{equation} Gain=w(P^{k-1})-w(P^k) \tag{2.40} \end{equation}\] Esta ganancia del clúster debe ser minimizada.
La configuración del clúster óptimo puede ser identificada por el “codo” que corresponde a la disminución significativa de las primeras diferencias de la ganancia del clúster contra el número de clústeres. Este “codo” puede ser identificada por un pico significante en las segundas diferencias de la ganancia del clúster.
2.6.27 Índice de Dunn
El índice de Dunn (Dunn, 1974) define un ratio entre la distancia mínima entre clústeres y la distancia máxima intraclúster. Es decir, \[\begin{equation} Dunn=\frac{\min_{1\leq i<j \leq q}d(C_i,C_j)}{\max_{1\leq k\leq q}diam(C_k)} \tag{2.41} \end{equation}\] donde \(d(C_i,C_j)\) es la función de la diferencia entre dos clústeres \(C_i\) y \(C_j\), definida como \(d(C_i,C_j)=\min_{x\epsilon C_i, y\epsilon C_j}\) y \(diam(C)\) es el diámetro del clúster, que puede ser considerado una medida de dispersión del clúster. Se puede definir de la siguiente manera: \[ diam(C)=\max_{x,y\epsilon C}{d(x,y)} \]
Si tenemos clústeres compactos y bien separados, se espera que el diámetro de los clústeres sea pequeño y la distancia entre los clústeres sea grande. Por eso, el índice debe ser maximizado.
2.6.28 Estadístico de Hubert
El estadístico de Hubert (L. Hubert & Arabie, 1985) es el coeficiente de correlación entre cualquier par de matrices. Cuando dos matrices son simétricas, este índice puede ser escrito como: \[\begin{equation} \Gamma(P,Q)=\frac{1}{N_t}\sum_{i=1}^{n-1}{P_{ij}Q_{ij}} \tag{2.42} \end{equation}\] para todo \(i< j\) y donde \(P\) es la matriz de proximidad o distancias entre las observaciones. \(Q\) es una matriz \(n \times n\) cuyo elemento \((i,j)\) es igual a la distancia entre los puntos representativos \((v_{ci},v_{cj})\) de los clústeres a los que pertenecen los objetos \(x_i\) y \(x_j\).
Para \(q=1\) o \(q=n\), el índice no está definido. El estadístico de Hubert normalizado es: \[\begin{equation} \overline{\Gamma}=\frac{\sum_{i=1}^{n-1}(P_{ij}-\mu_P)(Q_{ij}-\mu_Q)}{\sigma _P\sigma _Q} \tag{2.43} \end{equation}\]
donde \(\mu_P\),\(\mu_Q\),\(\sigma_P\),\(\sigma_Q\) son las respectivas medias y varianzas de las matrices \(P\) y \(Q\).
Este índice toma valores entre -1 y 1. Si \(P\) y \(Q\) no son simétricas, entonces todas las sumas se extienden sobre todas las entradas \(n^2\) y \(N_t=n^2\) (Bezdek & Pal, 1998).
Altos valores del \(\Gamma\) normalizado indican la existencia de clústeres compactos. En la gráfica del \(\Gamma\) normalizado contra \(k\) (\(k\) es el número de clústeres), se busca un “codo” que corresponda a un aumento grande del \(\Gamma\) normalizado al variar \(k\) de 2 a \(qmax\), donde \(qmax\) es el máximo número de clústeres posible. El número de clústeres al cual ocurre el “codo” es un indicador del número de clústeres óptimo (Haldiki et al., 2002).
2.6.29 Índice SD
El índice de validación SD está basado en los conceptos de dispersión promedio para clústeres y separación total entre clústeres. Se computa empleando la siguiente expresión: \[\begin{equation} SDindex(q)=\alpha Scat(q)+Dis(q) \tag{2.44} \end{equation}\] donde \(Scat(q)\) es el promedio de la distancia intraclúster. Un valor pequeño para este término indica clústeres compactos. \(Dis(q)\) es la distancia entre clústeres. Y \(\alpha\) es un factor de peso igual a \(Dis(qmax)\) donde \(qmax\) es el máximo número de clústeres de entrada. El número de clústeres, \(q\), que minimiza el índice de arriba puede ser considerado como un valor óptimo para el número de clústeres presentes en la base de datos.
2.6.30 Índice SDbw
El índice de validación SDbw está basado en el criterio de compacto y separación entre clústeres.
\[\begin{equation} SDbw(q)=Scat(q)+Density.bw(q) \tag{2.45} \end{equation}\]
donde \(Density.bw(q)\) es la densidad entre clústeres, definida de la siguiente manera: \[\begin{equation} Density.bw(q)=\frac{1}{q(q-1)}\sum_{i=1}^{q}\left(\sum_{j=1,i\neq j}^{q}\frac{density(u_{ij})}{max(density(c_i),density(c_j))}\right) \tag{2.46} \end{equation}\]
donde \(u_{ij}\) es el punto de la mitad del segmento definido por los clústeres centroides \(c_i\) y \(c_j\). Y \[\begin{equation} density(u_{ij})=\sum_{l=1}^{n_{ij}}f(x_l,u_{ij}) \tag{2.47} \end{equation}\]
donde \(n_{ij}\) es el número de duplas que pertenecen a los clústeres \(C_i\) y \(C_j\). Y \(f(x_l,u_{ij})\) es igual a 0 si \(d(x,u_ij)>Stdev\) y 1 en caso contrario. Finalmente, \(Stdev\) es la desviación estándar promedio de los clústeres; es decir,
\[\begin{equation} Stdev=\frac{1}{q}\sqrt{\sum_{k=1}^{q}{\left \| \sigma ^k \right \|}} \tag{2.48} \end{equation}\]
El número de clústeres \(q\) que minimiza \(SDbw\) es considerado el valor óptimo de clústeres para esa base de datos (Halkidi & Vazirgiannis, 2001).
Si la medida aumenta con el número de clústeres, como en el caso del índice D y el índice de Hubert, entonces encontrar el mínimo o máximo en una gráfica no es suficiente. Un cambio significativo en el valor de la medida, visto como el “codo” en la gráfica, indica los mejores parámetros para el clústering.
Referencias
En este contexto se emplean como sinónimos de características el término en inglés features. Si estás más acostumbrado al lenguaje que se emplea en estadística, un sinónimo para característica es variable. De hecho, recuerda que una variable se define como una característica de los individuos bajo estudio. ↩︎
Esta es la norma vectorial de orden 2.↩︎
Esta es la razón por la que los datos originales deben ser centrados, como se discutirá más adelante. Es decir, se emplean variables centradas (se resta la media) y escaladas (divididas por su desviación estándar) para evitar que las escalas de medición de las variables afecten el resultado, a esto lo llamaremos estandarizar los datos.↩︎
Esto se conoce como la “maldición de la dimensionalidad”. ↩︎
A esta distancia también se le denomina como la distancia del tablero de ajedrez, ya que el número mínimo de movimientos que necesita un rey para ir de una casilla a otra es igual a la distancia de Chebyshev.↩︎
En la práctica, la distancia de Chebyshev se utiliza mucho en aplicaciones de logística en especial la de almacenes, ya que se asemeja mucho al tiempo que tarda una grúa en mover un objeto.↩︎
Esta es la norma vectorial de orden 1.↩︎
Los creadores de esta distancia (Lance & Williams, 1967) le pusieron el nombre de su ciudad natal.↩︎
Algunos autores, incorrectamente, llaman a esto normalizar.↩︎
En este contexto una aproximación implica tanto el algoritmo seleccionado, la medida de distancia, como el número de clústeres \(q\).↩︎
Recuerda que en este contexto el centro se conoce como el centroide.↩︎
Sin embargo, al igual que las Sumas de Cuadrados y los Cuadrados medios en el modelo ANOVA o la tabla ANOVA de un modelo de regresión, la suma de cuadrados dentro del grupo está influida por el número de observaciones. A medida que aumenta el número de observaciones, la suma de cuadrados es mayor. Por lo tanto, la \(WSS\) no se puede emplear para comparar ejercicios de formación de clústeres con diferentes números de observaciones.↩︎
Una traducción sería brecha, pero en la literatura se conoce más como el estadístico Gap.↩︎
Cualquiera de las medidas de distancia estudiadas funciona en esta medida de cohesión.↩︎
No se necesita calcular la distancia con respecto al clúster en el que está el individuo \(i\) (\(C_i\)).↩︎
Como se mencionó anteriormente, en este contexto una aproximación implica: un algoritmo de construcción, una medida de distancia y un número de clústeres \(q\).↩︎
Es decir, \(BGSS_j\)= \(\sum_{k=1}^q n_k(c_{kj}-\overline{x}_j)^2\).↩︎
En otras palabras, \(TSS_j\)= \(\sum_{i=1}^n (x_{ij}-\overline{x}_j)^2\).↩︎