10 Modelo de Isolation Forest para detectar anomalías

10.1 Introducción

En los Capítulos 8 y 9 estudiamos técnicas para detectar anomalías con origen en los modelos de aprendizaje de máquina. La primera técnica de la distancia kNN se basa en la distancia para encontrar anomalías, lo cual le permite encontrar anomalías globales. Por otro lado, el LOF y el DBSCAN son métodos basados en densidad que permiten encontrar anomalías locales.

En este capítulo estudiaremos otra técnica que también es de origen en el aprendizaje de máquina que emplea una filosofía totalmente diferente: Isolation Forest. Isolation Forest es un método de aprendizaje no supervisado que está inspirado en el algoritmo de clasificación y regresión Random Forest⁷⁴. El Random Forest es un método de ensamblaje que combina múltiples árboles de decisión para mejorar la precisión y robustez de las predicciones. La idea detrás de un árbol de decisión es dividir los datos en subconjuntos basados en características específicas, creando una estructura de árbol donde cada nodo representa una característica y cada rama representa una decisión basada en esa característica. El objetivo es llegar a una predicción o clasificación en las hojas del árbol. El Random Forest crea múltiples árboles de decisión utilizando diferentes subconjuntos de datos y características, y luego combina las predicciones de todos los árboles para obtener una predicción final más precisa.

Al igual que en Random Forest, un modelo Isolation Forest está formado por la combinación de múltiples árboles llamados isolation trees (árboles de aislamiento). La idea principal detrás de Isolation Forest es que las anomalías son más fáciles de aislar que las observaciones normales. Por lo tanto, un árbol de aislamiento intenta separar todas las observaciones dividiendo aleatoriamente la región en sectores cada vez más pequeños. La observación que se pueda separar más fácilmente de las demás se considerará como anómala. El principio básico de Isolation Forest es que las anomalías suelen requerir menos particiones para ser aisladas que las observaciones normales.

En la Sección 10.2 presentamos una introducción a los Isolation Trees para después continuar en la Sección 10.3 con el concepto de Isolation Forest y posteriormente mostrar cómo se implementa este método en R.

10.2 Isolation Trees

Un árbol de aislamiento (Isolation Tree) tiene como objetivo aislar las observaciones atípicas, para lo cual de manera recursiva separa las observaciones. La observación que se pueda separar más fácilmente de las demás se considerará como anómala.

Un árbol de aislamiento intenta separar todos los puntos dividiendo aleatoriamente la región (el espacio de los datos) en sectores cada vez más pequeños. El árbol de aislamiento elige una variable (característica o feature) y divide las observaciones empleando un valor aleatorio para la característica. Y así continúa la división aleatoria hasta que cada observación se encuentra dentro de su propia subregión, o cada subregión contiene un número máximo de observaciones previamente establecido.

Para entender este algoritmo, veamos un ejemplo. Supongamos que contamos con una muestra de 5 observaciones y dos variables: \(x_1\) y \(x_2\). Además, supongamos que nuestro objetivo es tener al final del proceso solo una observación para cada subregión final (hoja del árbol). En el panel a) de la Figura 10.1 se presenta la muestra con 5 observaciones. Supongamos que el algoritmo escoge aleatoriamente la variable \(x_1\) y divide los datos con un valor aleatorio de 20 (Ver panel b) de la Figura 10.1). Esto divide la muestra en dos. Para valores de \(x_1\) mayores que 20 solo se encuentra una observación (observación en rojo) y para la otra región (\(x_1 < 20\)) se encuentran 4 observaciones. Como la subregión de la derecha ya alcanzó una observación, esta no se seguirá dividiendo. En otras palabras, la observación en rojo ya fue aislada. Entonces continuamos con la otra región (\(x_1 < 20\)).

Figura 10.1: Ejemplo sobre el funcionamiento de un Isolation Tree

Fuente: elavoración propia.

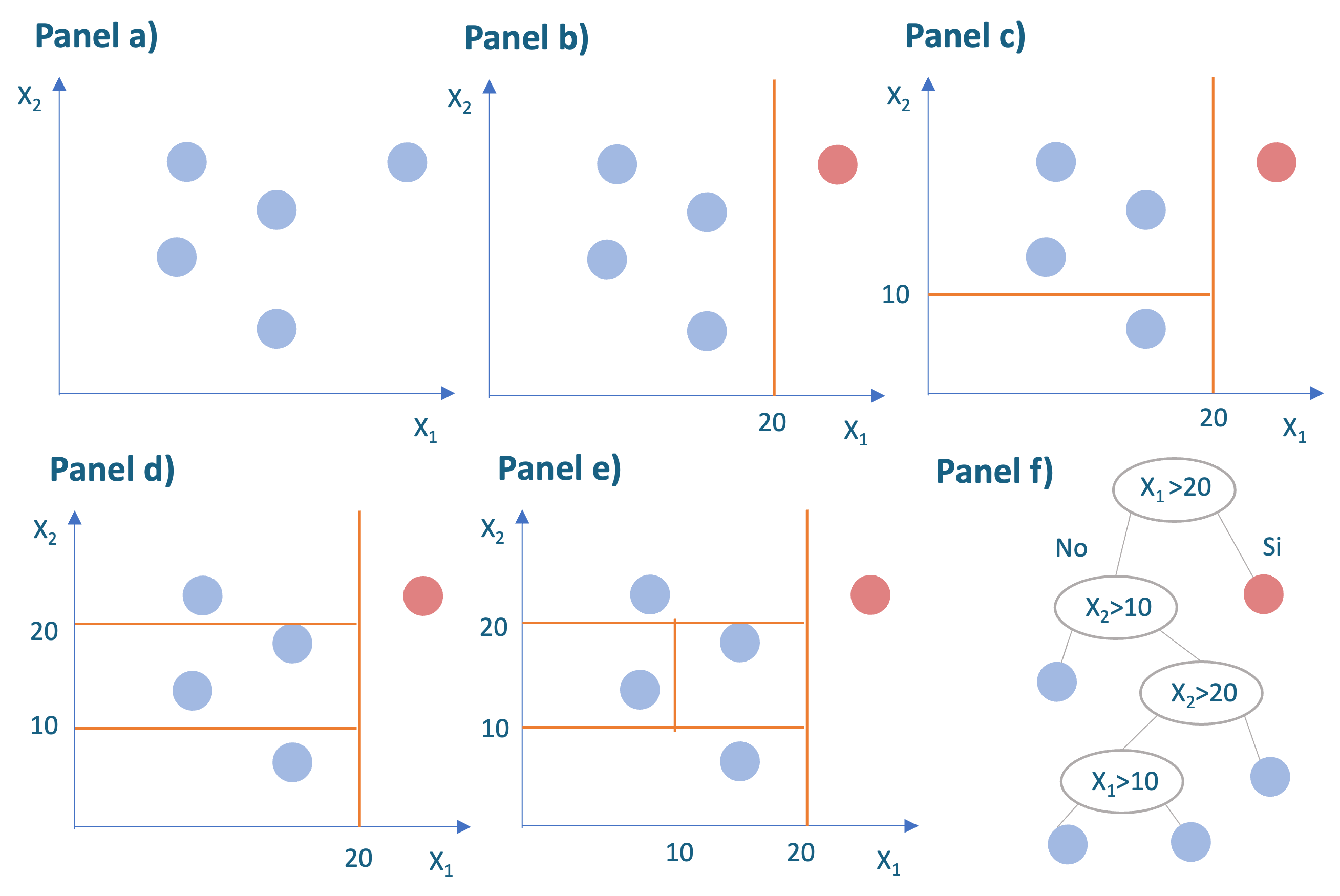
Ahora el algoritmo escogerá nuevamente aleatoriamente una variable y generará un valor aleatorio para partir la subregión. Supongamos que el algoritmo escoge aleatoriamente la variable \(x_2\) y genera un valor aleatorio de 10 (Ver panel c) de la Figura 10.1). El algoritmo continuará dividiendo las subregiones en las que se tengan más de una observación. En nuestro caso, supongamos que aleatoriamente se escoge nuevamente la variable \(x_2\) y genera un valor aleatorio de 20 (Ver panel d) de la Figura 10.1). Finalmente, se escoge la característica \(x_1\) y un valor aleatorio de 10 (Ver panel e) de la Figura 10.1). El algoritmo ha terminado de aislar todas las observaciones. Nota que la observación en rojo, la primera que aislamos, fue la más fácil de aislar y por eso se considerará como un outlier.

En el panel f) de la Figura 10.1 se presentan todos los pasos realizados con un diagrama de árbol, de ahí el nombre del algoritmo.

Una vez se ha construido un Isolation Tree, se construye un score de anomalía para cada observación. Recordemos que un Isolation Tree mide el “aislamiento” de una observación en función de la rapidez con la que puede separarse mediante una secuencia de divisiones aleatorias.

El número de divisiones aleatorias necesarias para separar cada observación es un número entero positivo denominado longitud del camino. La longitud máxima posible del camino depende en parte del tamaño de la muestra empleada para construir el árbol y no tiene una interpretación intuitiva. Por eso, típicamente esas longitudes de los caminos se presentan normalizadas; es decir, entre 0 y 1. Si la puntuación es cercana a 1, entonces la longitud del camino es muy pequeña, lo que significa que el punto se aisló fácilmente con divisiones aleatorias y, por lo tanto, es más probable que sea una anomalía. Si la puntuación es cercana a 0, entonces la longitud del camino es grande, lo que implica que el punto no era anómalo.

10.3 Isolation Forest

Regresando al ejemplo que discutimos anteriormente (Ver Figura 10.1). Recordemos que ese aislamiento es fruto de un proceso aleatorio. Por ejemplo, podríamos tener particiones diferentes dependiendo del proceso aleatorio. En la Figura 10.2 se presentan en los paneles b) y c) Isolation Trees con particiones diferentes.

Figura 10.2: Ejemplos de diferentes Isolation Trees para la misma muestra

Fuente: elavoración propia.

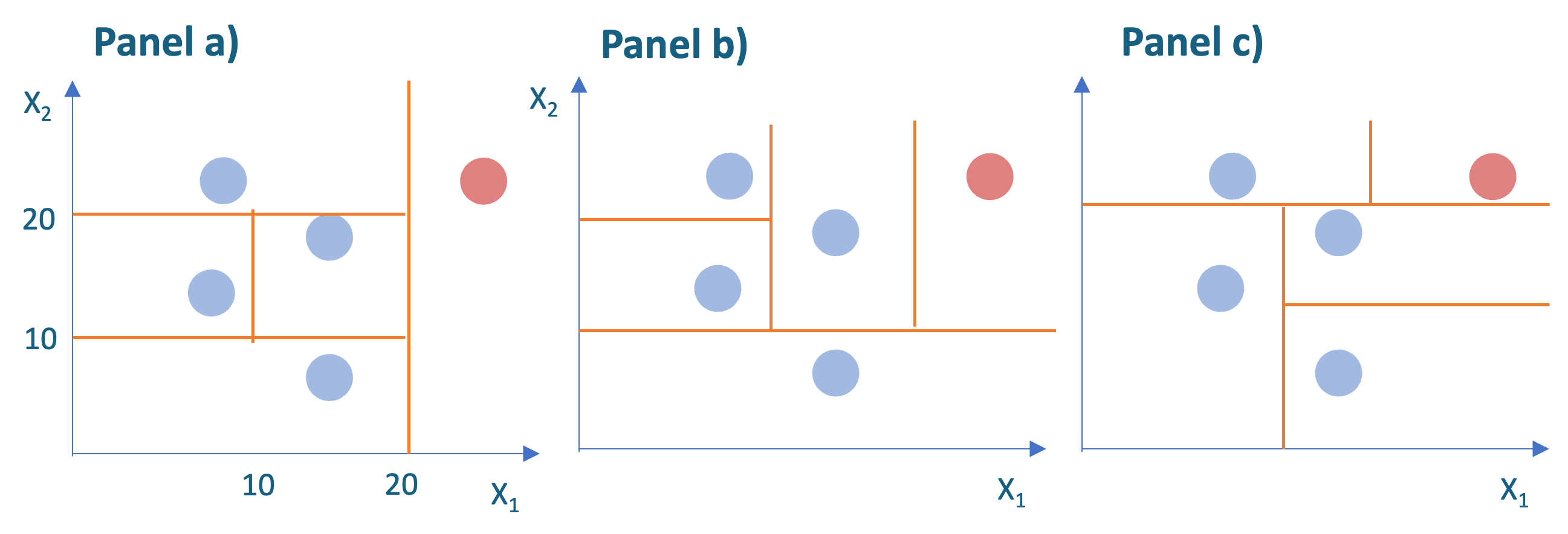
Como lo discutimos, un Isolation Tree “individual” mide el grado de anomalía de una observación en función del número de divisiones aleatorias necesarias para aislarlo. Y como acabamos de ver en la Figura 10.2, las particiones dependen de los valores aleatorios que asigna el algoritmo. Por lo tanto, la puntuación de anomalía de un solo árbol puede ser inestable.

Siguiendo la misma idea de un Random Forest, F. T. Liu et al. (2008) propusieron emplear muchos árboles de aislamiento en vez de uno solo; es decir, un bosque de árboles de aislamiento (de ahí el nombre de Isolation Forest). Un Isolation Forest se compone de muchos Isolation Trees, cada uno de los cuales “crece” utilizando una muestra diferente de los datos originales.

En este caso, la puntuación de anomalía se genera para cada árbol y luego se calcula la media de todos los árboles cultivados en el bosque. Emplear un bosque para generar muchas puntuaciones y promediarlas tiene dos ventajas. En primer lugar, mientras que los árboles individuales pueden ser sensibles a patrones fortuitos en la muestra de datos, la puntuación media es muy estable. En segundo lugar, nunca se utilizan los datos completos para construir un árbol, por lo que es posible obtener puntuaciones de anomalías mucho más rápidamente. Es decir, un Isolation Forest es computacionalmente más eficiente y por tanto puede emplear grandes conjuntos de datos.

Cuando se entrena un Isolation Forest surge la pregunta de cuántos árboles deberíamos “cultivar”. Típicamente, el score de la anomalía para cada observación tiende a converger después de haber cultivado un número suficientemente grande de árboles. En la práctica, siguiendo a F. T. Liu et al. (2008), es común emplear 100 árboles para empezar a investigar si los scores están convergiendo o no. En otras palabras, en la práctica se empieza con 100 árboles para determinar si los scores ya son estables entre los árboles o no. Y si no es estable se emplean más árboles. Es decir, deberíamos entrenar varios Isolation Forest con diferentes números de árboles, y comparar si la puntuación cambia cuando se añaden más árboles. Si la puntuación cambia mucho, esto podría sugerir que se necesitan más árboles. En la siguiente sección mostraremos un ejemplo de cómo hacer esto en R.

10.4 Implementación en R

Para realizar un ejemplo práctico seguiremos usando los mismos datos que empleamos en la mayoría de los Capítulos de este libro. Los datos provienen de Hofmann (1994) y se encuentran en el archivo datos_credito.RData que se puede descargar de la página web del libro (https://www.icesi.edu.co/editorial/deteccion-anomalías). La descripción de las variables se encuentra en la Sección 2.4. Carguemos los datos:

load("./datos/datos_credito.RData")

Los datos están cargados en el objeto de clase data.frame que denominamos german. Ese objeto tiene 14 variables y 1000 clientes. Seleccionemos solo las variables cuantitativas para poder aplicar las técnicas estudiadas en las secciones anteriores. Empleemos la función select_if() del paquete dplyr (Wickham et al., 2021) para hacer esta tarea más sencilla.

library(dplyr)
german_cuanti <- german %>% 
     select_if(is.numeric)

Trabajaremos con una base de datos con 6 variables y 1000 observaciones.

El paquete isotree (Cortes, 2024) nos permite entrenar tanto el modelo de Isolation Tree como el de Isolation Forest.

Para ambos casos, el Isolation Tree o el Isolation Forest, podemos emplear la función isolation.forest() La función típicamente incluye los siguientes argumentos:

isolation.forest(data, ntrees, ndim, seed )

donde:

data: Corresponde a los datos, que pueden ser clase data.frame, matrix.
ntrees: Corresponde al número de árboles que serán “cultivados”. El valor por defecto es ntrees = 500
ndim: El número de variables que se emplearán para realizar la separación de las subregiones en cada nodo del árbol (split). El valor por defecto es ndim = 1.
seed: Semilla que se utilizará para la generación de números aleatorios.

Como se discutió anteriormente, para el número de árboles en un Isolation Forest se puede emplear 100 como lo recomiendan F. T. Liu et al. (2008). F. Liu et al. (2010) sugieren emplear 10 árboles.

De acuerdo a Cortes (2024), el número de árboles ideal debería crecer a medida que hay más variables, se incluyen variables categóricas⁷⁵ y el número de variables que se emplearán a la misma vez para separar las subregiones (argumento ndim de la función).

Cortes (2024) argumenta que una buena manera de determinar si se ha seleccionado un número adecuado de árboles, es mirar la distribución de los scores de anomalía de todas las observaciones. Ellos argumentan, que si el promedio de dichos scores es inferior a 0.5 es es señal de que el modelo necesita más árboles.

Por otro lado, el número de variables que se emplearán para realizar la separación de las subregiones en cada nodo del árbol (split) es otro parámetro importante para este algoritmo. Si se emplea una variable (el valor por defecto de la función isolation.forest()), se entrenará el algoritmo originalmente sugerido por F. T. Liu et al. (2008). F. T. Liu et al. (2010a) sugieren emplear dos variables en vez de una. Y Hariri et al. (2019) sugieren un número bajo de variables, 2 o 3. Hariri et al. (2019) llamaron a estos modelos con más de una variable en cada split como el modelo Extended Isolation Forest.

En la práctica, deberemos “jugar” con estos dos parámetros, hasta que encontremos que los resultados converjan y sean robustos a cambios pequeños en ellos.

Regresando a nuestro ejemplo un Isolation Tree puede ser entrenado empleando el siguiente código:

library(isotree)
# Entrenar un Isolation Tree
iso_tree <-  isolation.forest(german_cuanti,
                              ndim=1, ntrees=1, seed = 1234)

iso_tree

## Isolation Forest model
## Consisting of 1 trees
## Numeric columns: 6

Los scores para cada observación se pueden calcular empleando la función predict.isolation_forest del paquete isotree de la siguiente manera:

# Calcular scores de anomalía
scores <- predict(iso_tree, german_cuanti)

Estos scores corresponden a un objeto de clase numeric que puede ser analizado de una manera tradicional. Por ejemplo,

# Estadísticas descriptivas de los scores
summary(scores)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.3664  0.4049  0.4417  0.4758  0.5220  0.8075

# Observación con el score más grande
which.max(scores)

## 757 
## 757

Según este algoritmo, la observación 757 tiene el score de anomalía más grande (0.81). Envés de continuar con el análisis de este árbol, calculemos un Isolation Forest que sabemos tiene mejores propiedades que un solo árbol.

El siguiente código entrena un Isolation Forest con 100 árboles y calcula el score de anomalía promedio:

# Entrenar un Isolation Forest
iso_forest_100 <-  isolation.forest(german_cuanti,
                              ndim=1, ntrees=100, seed = 1234)

iso_forest_100

## Isolation Forest model
## Consisting of 100 trees
## Numeric columns: 6

# Calcular scores de anomalía
scores_100 <- predict(iso_forest_100, german_cuanti)

En este caso el promedio de los scores de anomalía es relativamente cercano a 0.5 (0.48), lo cual según Cortes (2024) es indicio de que el número de árboles es adecuado.

Por otro lado, para seguir la práctica que se discutió arriba, entrenemos un Isolation Forest con 500 árboles y comparemos los respectivos scores de anomalía para inspeccionar si son parecido o no. Recuerda que antes discutimos que el score de anomalías de un Isolation Forest no suele cambiar después de que haya crecido un cierto número de árboles. Esto se denomina convergencia, y puede comprobarse comparando las puntuaciones generadas por bosques con diferentes números de árboles. Si las puntuaciones difieren mucho, esto podría sugerir que se necesitan más árboles.

Creemos los scores de anomalías para bosques con 500 y 1000 árboles con el siguiente código:

# Entrenar un Isolation Forest 500 árboles
iso_forest_500 <-  isolation.forest(german_cuanti,
                              ndim=1, ntrees=500, seed = 1234)

# Calcular scores de anomalía 
scores_500 <- predict(iso_forest_500, german_cuanti)
mean(scores_500)

## [1] 0.4777459

# Entrenar un Isolation Forest 1000 árboles
iso_forest_1000 <-  isolation.forest(german_cuanti,
                              ndim=1, ntrees=1000, seed = 1234)

# Calcular scores de anomalía
scores_1000 <- predict(iso_forest_1000, german_cuanti)
mean(scores_1000)

## [1] 0.4776192

Nota que en todos los tres casos el promedio de los scores de anomalía es relativamente cercano a 0.5. En la Figura 10.3 se muestra la comparación de los scores de anomalía para los bosques con 100, 500 y 1000 árboles. En la Figura 10.3 podemos ver que los scores son algo diferentes entre los bosques de 100 y 500 árboles⁷⁶. No obstante, para los bosques con 500 y 1000 árboles son relativamente parecidos, esto implicaría que el bosque con 500 árboles ya alcanzó la convergencia⁷⁷. En otras palabras, un bosque de 1000 árboles ofrece pocas ventajas sobre uno de 500 árboles.

Figura 10.3: Comparación de los scores de anomalía para los modelos de Isolation Forest con 100, 500 y 1000 árboles

Fuente: elavoración propia.

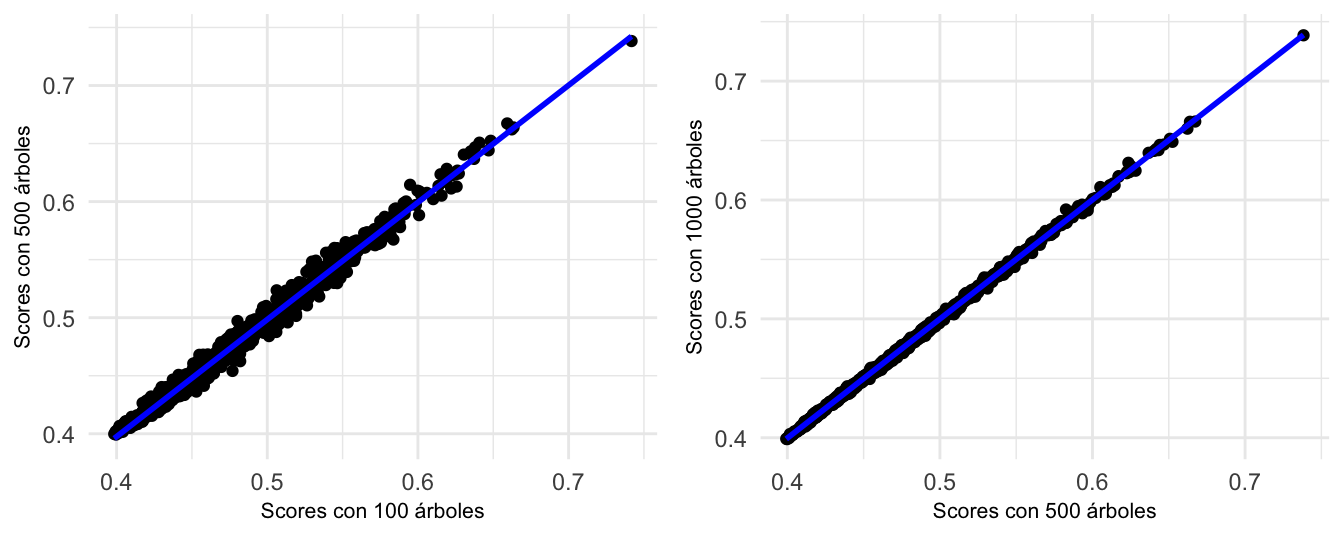
Ahora, podemos emplear el bosque con 500 árboles para realizar nuestro análisis de anomalías. Por ejemplo, las 10 observaciones con el score de anomalía más alto se pueden encontrar de la siguiente manera:

data.frame(scores_500) %>% 
  top_n(10) %>% 
  arrange(desc(scores_500))

##     scores_500
## 757  0.7383126
## 66   0.6673362
## 591  0.6638848
## 654  0.6622151
## 916  0.6524073
## 918  0.6507702
## 928  0.6467596
## 187  0.6441389
## 206  0.6432550
## 891  0.6419446

La observación 757 tiene el score de anomalía más grande (0.74). Esta observación debería estudiarse en más detalle.

10.5 Comentarios finales

En este capítulo hemos estudiado otro algoritmo para detectar anomalías que tiene su origen en el aprendizaje de máquina, el Isolation Forest. Este algoritmo puede identificar anomalías univariadas y multivariadas. También permite identificar anomalías puntuales, anomalías locales o contextuales y anomalías colectivas⁷⁸.

Este modelo, más que un modelo, es una familia de modelos en la que los investigadores han desarrollado recientemente grandes contribuciones. Existen diferentes variantes del Isolation Forest, conocido en la literatura también como iForest. Ya hemos discutido el Extended Isolation Forest (EIF) que implica emplear dos variables en cada split de los datos. El EIF lo podemos implementar con la función isolation.forest() empleando el argumento ndim=2 y los argumentos coefs=“uniform” y standardize_data=False. En este caso debemos estar seguros nuevamente de que el algoritmo converge, y no necesariamente convergerá con el mismo número de árboles que la versión anterior. ¡Inténtalo!

Existen otras diferentes versiones del modelos iForest que se pueden implementar en con el paquete isotree:

Split-Criterion iForest (SCiForest): Este modelo realiza las divisiones de las regiones con respecto a un hiperplano elegido al azar en lugar de hacer solo divisiones paralelas al eje. Este modelo propuesto por F. T. Liu et al. (2010b) se puede implementar con la función isolation.forest() empleando los argumentos: ndim=2, coefs=“normal”, ntry=10, penalize_range=True y prob_pick_avg_gain=1.
Fair-Cut Forest (FCF): Este modelo propuesto por Cortes (2021) elige el punto de división según criterios relacionados con las desviaciones estándar o la densidad. Este modelo propuesto por F. T. Liu et al. (2010b) se puede implementar con la función isolation.forest() empleando los argumentos: ndim=1, coefs=“normal”, ntry=1 y prob_pick_pooled_gain=1.
Robust Random-Cut Forest (RRCF): Guha et al. (2016) propusieron este método que implica elegir la variable a dividir con una probabilidad proporcional al rango que abarca en lugar de elegirla uniformemente al azar, siguiendo la idea de que las variables con un rango más amplio son más importantes en una distribución multivariante y más propensas a diferenciar valores atípicos. Este modelo propuesto se puede implementar con la función isolation.forest() empleando los argumentos: ndim=1 y prob_pick_col_by_range=1.

En todos los casos, al implementar estos algoritmos será importante chequear que el algoritmo tenga el número de árboles adecuados; es decir, que converja.

Estos modelos basados en bosques de Isolation Trees pueden adaptarse a los cambios en la distribución de los datos, por lo que son adecuados para supervisar entornos dinámicos. También son algoritmos flexibles al permitir el uso de variables cualitativas. Adicionalmente, estos bosques son robustos al ruido, lo que puede ser especialmente útil para detectar anomalías en flujos de datos en tiempo real.

Por otro lado, uno de los problemas de esta familia de algoritmos es que son modelos de “caja negra”. Es decir, comprender el razonamiento que subyace a su detección de anomalías es poco intuitivo. Esta falta de interpretación puede hacer que no sean útiles en industrias donde la transparencia de los algoritmos y la capacidad de explicarlos sean necesarios, como por ejemplo en los bancos y el sistema financiero o el sector salud.

Otro posible problema de los bosques de Isolation Trees puede aparecer cuando contamos con muchas variables (alta dimensionalidad de los datos). En estos casos las demandas de capacidad de cómputo de estos modelos serán muy altas y en ocasiones prohibitivas.

El algoritmo de Isolation Forest representa un avance significativo en la detección de anomalías de alta dimensión (muchas variables). Su eficiencia y escalabilidad lo convierten en una alternativa atractiva frente a métodos basados en distancias o densidades. Sin embargo, como todo modelo, requiere una validación cuidadosa y debe complementarse con otras técnicas y con el conocimiento del negocio. Emplear al mismo tiempo diferentes técnicas de detección de anomalías permite tener una mirada desde diferentes ángulos al problema de detección de anomalías.

En el Capítulo 11 presentaremos unas reflexiones sobre todas las herramientas que hemos estudiado y sobre las perspectivas de esta amplia rama del business analytics. Por ahora recuerda que todas las herramientas estudiadas hasta el momento son útiles para detectar anomalías, cada una tiene unas fortalezas y debilidades frente a las otras. Por eso, para responder una pregunta de negocios que implique la tarea de detección de anomalías siempre será importante contar con una caja de herramientas bien dotada de diferentes aproximaciones para encontrar las anomalías. Dependiendo de los datos y del contexto del negocio, existirán algunas herramientas que tengan más sentido que otras. En últimas, no existe una herramienta para la detección de anomalías que sea siempre mejor que las demás.

Referencias

Alonso, J. C., & Hoyos, C. C. (2025). Una introducción a los modelos de clasificación empleando r. Universidad Icesi. https://doi.org/https://doi.org/10.18046/EUI/bda.h.5

Cortes, D. (2021). Revisiting randomized choices in isolation forests. https://arxiv.org/abs/2110.13402

Cortes, D. (2024). Isotree: Isolation-based outlier detection. https://CRAN.R-project.org/package=isotree

Guha, S., Mishra, N., Roy, G., & Schrijvers, O. (2016). Robust random cut forest based anomaly detection on streams. International Conference on Machine Learning, 2712–2721.

Hariri, S., Kind, M. C., & Brunner, R. J. (2019). Extended isolation forest. IEEE Transactions on Knowledge and Data Engineering, 33(4), 1479–1489.

Hofmann, H. (1994). Statlog (German Credit Data). UCI Machine Learning Repository.

Liu, F. T., Ting, K. M., & Zhou, Z.-H. (2008). Isolation forest. 2008 Eighth Ieee International Conference on Data Mining, 413–422.

Liu, F. T., Ting, K. M., & Zhou, Z.-H. (2010a). On detecting clustered anomalies using sciforest. Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2010, Barcelona, Spain, September 20-24, 2010, Proceedings, Part II 21, 274–290.

Liu, F. T., Ting, K. M., & Zhou, Z.-H. (2010b). On detecting clustered anomalies using SCiForest. In J. L. Balcázar, F. Bonchi, A. Gionis, & M. Sebag (Eds.), Machine learning and knowledge discovery in databases (pp. 274–290). Springer Berlin Heidelberg.

Liu, F., Ting, K., & Zhou, Z. (2010). Can isolation-based anomaly detectors handle arbitrary multi-modal patterns in data. Technical Report.

Wickham, H., François, R., Henry, L., & Müller, K. (2021). Dplyr: A grammar of data manipulation. https://CRAN.R-project.org/package=dplyr

Para una introducción al Random Forest puedes ver el Capítulo 8 de Alonso & Hoyos (2025).↩︎
¡Sí! este algoritmo puede emplear variables cualitativas. Para comparar los resultados con los otros algoritmos, en este capítulo solo empleamos las variables cuantitativas. Para incluir las variables cualitativas en la función isolation.forest() debes emplear el argumento categ_cols. Mira la ayuda de esta función para ver somo emplear ese argumento.↩︎
Los puntos están algo alejados de la línea de 45 grados.↩︎
Podríamos seguir chequeando exactamente dónde se alcanza la convergencia, pero realmente eso no es de utilidad para nuestra finalidad de encontrar las anomalías. Lo único importante para cumplir nuestro objetivo es tener claro que el algoritmo ya convergió.↩︎
Si bien el algoritmo Isolation Forest ha sido construido para detectar anomalías puntuales y contextuales, también puede detectar anomalías colectivas si las características del grupo hacen que sean fáciles de aislar.↩︎