9 Modelo DBSCAN para detectar anomalías
9.1 Introducción
En el Capítulo 8 estudiamos dos métricas para detectar anomalías con origen en los modelos de aprendizaje de máquina: la distancia kNN y LOF. La primera técnica se basa en la distancia para encontrar anomalías, lo cual le permite encontrar anomalías globales. Por otro lado, el LOF es un método basado en densidad que permite encontrar anomalías locales.
En este capítulo estudiaremos el uso del modelo DBSCAN (Density-Based Spatial Clustering of Applications with Noise) para detectar anomalías. El DBSCAN es otra técnica basada en densidades que también permite encontrar anomalías locales. Intuitivamente, los métodos basados en densidad identifican regiones de alta concentración de datos y consideran como anomalías aquellos puntos que se encuentran en regiones de baja densidad. De hecho, a diferencia del LOF, el método que estudiaremos en este capítulo permite encontrar anomalías grupales. A diferencia del LOF que busca la densidad alrededor de cada punto y por eso identifica anomalías locales individuales, esta técnica se concentrará en grupos de observaciones, lo que permitirá encontrar anomalías locales grupales.
El modelo DBSCAN es un modelo diseñado para construir clústeres que puede ser empleado en la tarea de detección de anomalías. Es decir, este modelo permite realizar tanto la tarea de clústering72 como la detección de anomalías.
Inicialmente, el DBSCAN fue propuesto por Ester et al. (1996) para identificar clústeres de formas arbitrarias y con robustez ante datos ruidosos. Es decir, datos que no siguen el patrón general o la estructura subyacente de los datos. El ruido en este contexto se refiere a los individuos que no pertenecen claramente a ningún clúster o que pueden interferir con la identificación de clústeres con mayor definición. En otras palabras, una de las características de DBSCAN es poder trabajar con datos atípicos que, como veremos, el algoritmo termina no clasificando. Una vez que se empezó a usar este algoritmo para hacer clústering, se descubrió que también podía ser empleado para detectar anomalías.
En la Sección 9.2 presentamos el algoritmo DBSCAN de manera intuitiva y formal. En la Sección 9.3 presentamos su implementación en R.
9.2 El algoritmo DBSCAN
En general, este tipo de algoritmo basado en densidad se caracteriza por identificar regiones de alta densidad de individuos separadas por regiones de baja densidad en el espacio de datos (Ver Figura 9.1). Al encontrar esas regiones de alta densidad de datos, también encuentra aquellos puntos que no pertenecen a esas zonas de alta densidad (puntos grises en la Figura 9.1). Esas observaciones de baja densidad que no se pueden clasificar en clústeres corresponderán a los datos anómalos localmente; es decir, que no se parecen a sus vecinos.
Figura 9.1: Tipo de clústeres que puede encontrar DBSCAN
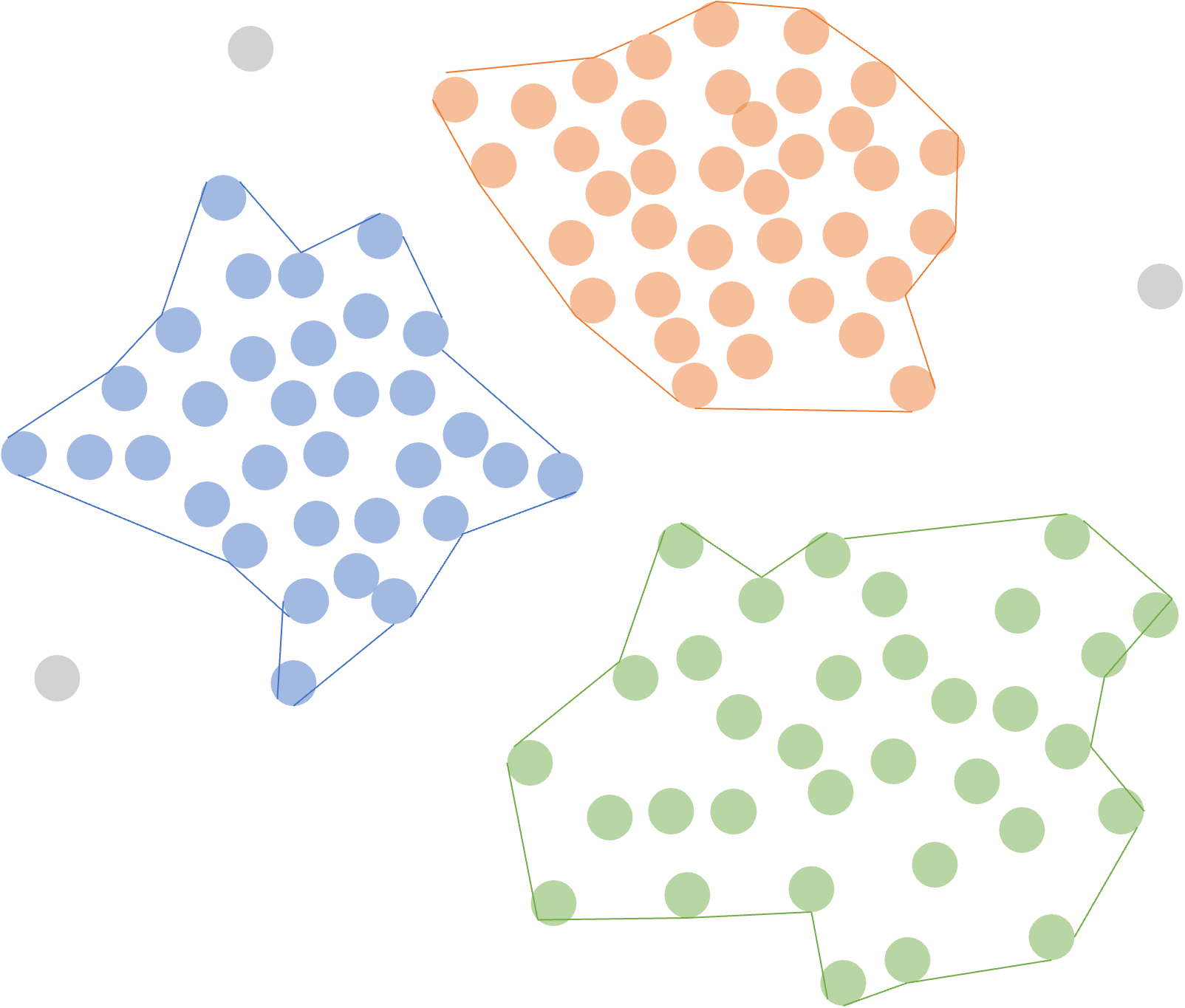
Así, DBSCAN, a diferencia de modelos tradicionales de clústering como los jerárquicos y k-means, puede lidiar con los valores anómalos (Alonso et al., 2025). Todos los valores anómalos serán identificados y marcados sin ser clasificados en ningún clúster. Por esta razón, DBSCAN también es empleado para la detección de anomalías (Kassambara, 2017).
Formalmente, el algoritmo de DBSCAN implica dos parámetros importantes: eps (\(\epsilon\)) y minPts. eps (\(\epsilon\)) representa el radio máximo del vecindario de una observación. Por otro lado, minPts es el número mínimo de puntos que deben estar dentro de la vecindad de un punto para que este sea considerado un punto central y, por tanto, se configure un clúster (incluyendo el mismo punto).
Intuitivamente, cada individuo en la muestra que tenga un número de vecinos (en el vecindario \(\epsilon\)) igual o mayor a minPts será marcado como un punto central (Ver Figura 9.2). Por otro lado, si un individuo \(w\) tiene un número de vecinos inferior a minPts, pero pertenece al vecindario \(\epsilon\) (\(\epsilon\)-neighborhood) de otro punto, entonces \(w\) será denominado un punto de frontera (border point) (Ver Figura 9.2). Y si un punto no es punto central (core point) ni uno en la frontera (border point), entonces será denominado ruido (noise point) o anomalía (Ver Figura 9.2). De esta manera, el algoritmo va asignando cada punto a un clúster o lo marca como anomalía. Para conocer el detalle de este algoritmo puedes ver el Capítulo 7 de Alonso et al. (2025).
Figura 9.2: Clasificación de individuos en el algoritmo DBSCAN con minPts = 6
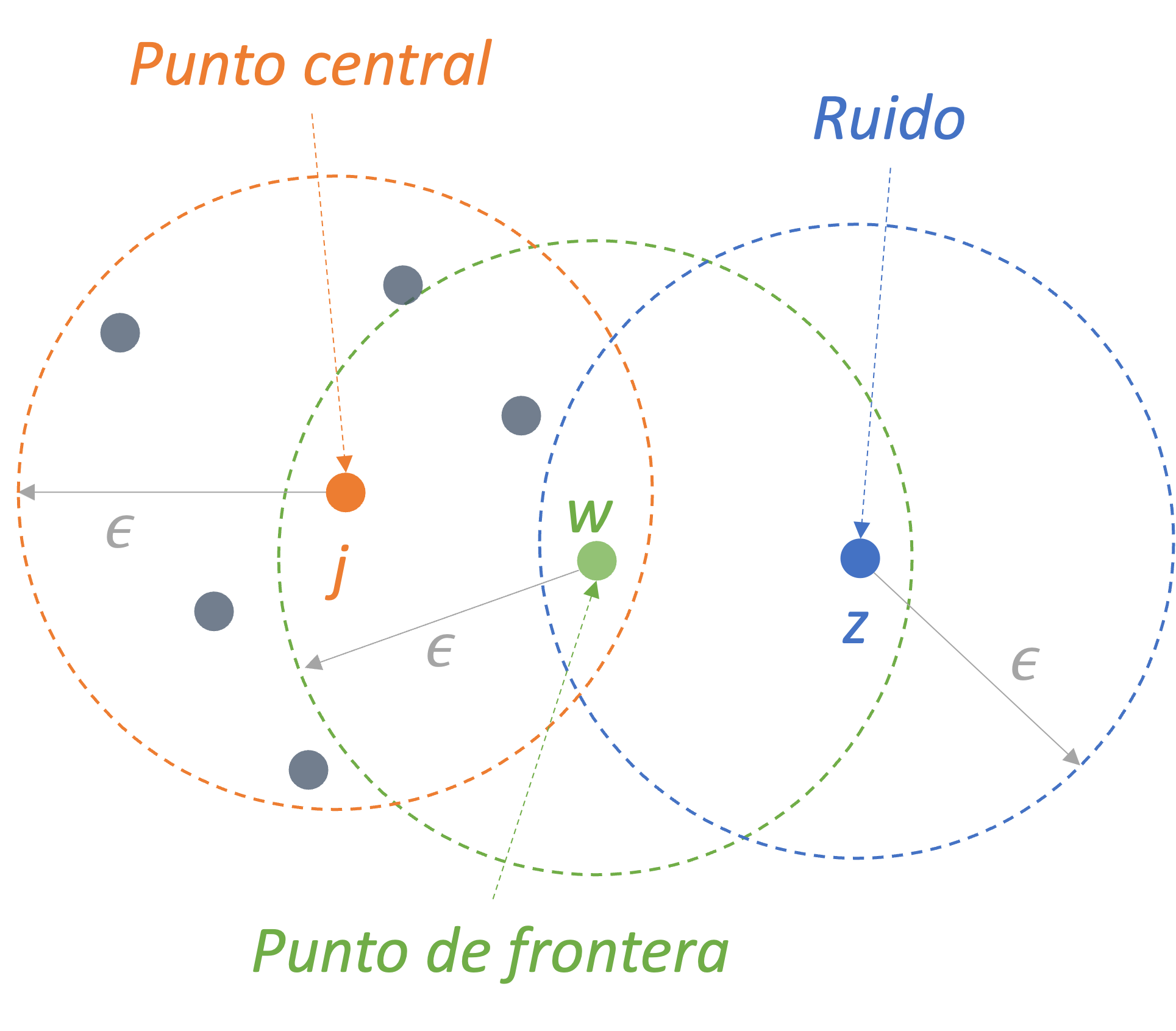
Una de las características del algoritmo DBSCAN es que este no requiere la definición previa del número de clústeres, al ser este un resultado del mismo algoritmo. De hecho, el número de clústeres óptimo (\(q\)) es resultado del valor óptimo del parámetro eps (\(\epsilon\)). Chen et al. (2020) sugiere emplear la media de las distancias de cada individuo a sus \(k\) vecinos más cercanos (distancia kNN) para encontrar dicho parámetro.
El algoritmo implica calcular la distancia kNN para cada individuo y diferentes valores del parámetro eps y posteriormente calcular la suma cuadrada de las distancias kNN. Empleando ese resultado, se busca el valor de eps que minimiza dicha suma.
9.3 Implementación en R
Para detectar anomalías con DBSCAN se requiere hacer el ejercicio de clústering, veamos en detalle cómo realizar el procedimiento de clusterización con DBSCAN en R. Si ya dominas esta técnica, puedes saltarte esta subsección. Si quieres estudiar en más detalle DBSCAN puedes consultar el Capítulo 7 de Alonso et al. (2025).
En este capítulo seguiremos empleando los mismos datos que trabajamos en los Capítulos 2, 3, 4 y 5. Los datos provienen de Hofmann (1994) y se encuentran en el archivo datos_credito.RData que se puede descargar de la página web del libro (https://www.icesi.edu.co/editorial/deteccion-anomalias). La descripción de las variables se encuentra en la Sección 2.4. Carguemos los datos:
Los datos están cargados en el objeto de clase data.frame que denominamos german. Ese objeto tiene 14 variables y 1000 clientes. Seleccionemos solo las variables cuantitativas para poder aplicar DBSCAN. Empleemos la función select_if() del paquete dplyr (Wickham et al., 2021) para hacer esta tarea más sencilla.
Recuerden que contamos con mil observaciones y 6 variables.
9.3.1 Algoritmo DBSCAN en R
Este algoritmo se puede implementar en R por medio de la función dbscan() del paquete dbscan (Hahsler et al., 2019). Pero antes de emplear esta función es necesario conocer cuál es el valor óptimo del parámetro eps. La propuesta de Chen et al. (2020) se puede implementar en R empleando la función n_clusters_dbscan del paquete parameters.
Esta función tiene los siguientes argumentos
donde:
x: objeto con datos de clase data.frame
standardize: si es TRUE se estandarizarán los datos, este es el valor por defecto.
incluir_factores: si es TRUE, las variables de clase factor se convierten en objetos numéricos para ser incluidas en los datos para determinar el número de clústeres. Por defecto, es igual a FALSE; es decir, se eliminan las variables que sean de clase factor. Esto se hace porque la mayoría de los métodos que determinan el número de conglomerados solo funcionan con variables cuantitativas.
min_size: el número mínimo de individuos (incluyendo al mismo individuo) requeridos en el vecindario \(\epsilon\) (\(\epsilon\)-neighborhood) para ser considerado como un punto central (core point). Por defecto, el valor es el 10% de la muestra (min_size = 0.1). Si se emplea un entero, este será el número de observaciones. Equivale al parámetro minPts.
eps_range: El rango sobre el cual se evaluarán los posibles valores del parámetro eps.
method: El método para escoger el parámetro eps óptimo. En nuestro caso, empleemos method = “SS” para que se calcule la suma cuadrada.
distance_method: El tipo de distancia a calcular. Este elemento es pasado a la función dist(). . Por defecto, el método es “euclidean”; los otros posibles valores son “maximum”, “manhattan”, “canberra”, “binary” y “minkowski”. No obstante, para el caso del algoritmo DBSCAN no se encuentra habilitada la opción para otra distancia.
El valor óptimo del parámetro eps (\(\epsilon\)) para el algoritmo DBSCAN y el método de la distancia kNN (Ver Sección 8.1) y empleando la distancia euclidiana lo podemos encontrar con el siguiente código empleando nuestros datos ya estandarizados (datos_est) y la distancia euclidiana.
library(parameters)
library(dbscan)
res_dbscan_knn <- n_clusters_dbscan(german_cuanti,
standardize = TRUE,
eps_range = c(0.001, 3),
min_size = 5,
distance_method = "euclidean",
method = "SS")Los resultados del eps óptimo los podemos visualizar imprimiendo el resultado en la consola o por medio de la Figura 9.3.
## eps n_Clusters total_SS
## 1 0.00100000 0 5994.000
## 2 0.06220408 0 5994.000
## 3 0.12340816 7 5904.835
## 4 0.18461224 10 5614.148
## 5 0.24581633 21 5381.524
## 6 0.30702041 21 5013.082
## 7 0.36822449 24 4717.736
## 8 0.42942857 32 4498.607
## 9 0.49063265 33 4225.445
## 10 0.55183673 32 4011.373
## 11 0.61304082 33 3853.884
## 12 0.67424490 32 3663.358
## 13 0.73544898 33 3511.788
## 14 0.79665306 34 3429.663
## 15 0.85785714 34 3372.487
## 16 0.91906122 10 4475.440
## 17 0.98026531 4 4352.314
## 18 1.04146939 6 4236.618
## 19 1.10267347 6 4167.380
## 20 1.16387755 7 4146.265
## 21 1.22508163 7 4113.196
## 22 1.28628571 6 4100.781
## 23 1.34748980 5 4078.374
## 24 1.40869388 6 4063.361
## 25 1.46989796 6 4050.378
## 26 1.53110204 6 4035.224
## 27 1.59230612 6 4036.018
## 28 1.65351020 6 4033.557
## 29 1.71471429 6 4036.916
## 30 1.77591837 2 4797.414
## 31 1.83712245 2 4809.183
## 32 1.89832653 2 4816.140
## 33 1.95953061 2 4817.710
## 34 2.02073469 2 4838.101
## 35 2.08193878 2 4846.380
## 36 2.14314286 2 4843.118
## 37 2.20434694 2 4862.773
## 38 2.26555102 2 4878.640
## 39 2.32675510 2 4895.874
## 40 2.38795918 2 4906.858
## 41 2.44916327 2 4906.858
## 42 2.51036735 2 4926.477
## 43 2.57157143 2 4915.415
## 44 2.63277551 2 4938.087
## 45 2.69397959 2 4939.577
## 46 2.75518367 2 4939.577
## 47 2.81638776 1 5963.098
## 48 2.87759184 1 5963.098
## 49 2.93879592 1 5963.098
## 50 3.00000000 1 5963.098Figura 9.3: Seleccionando el valor óptimo del parámetro eps por medio de la distancia kNN
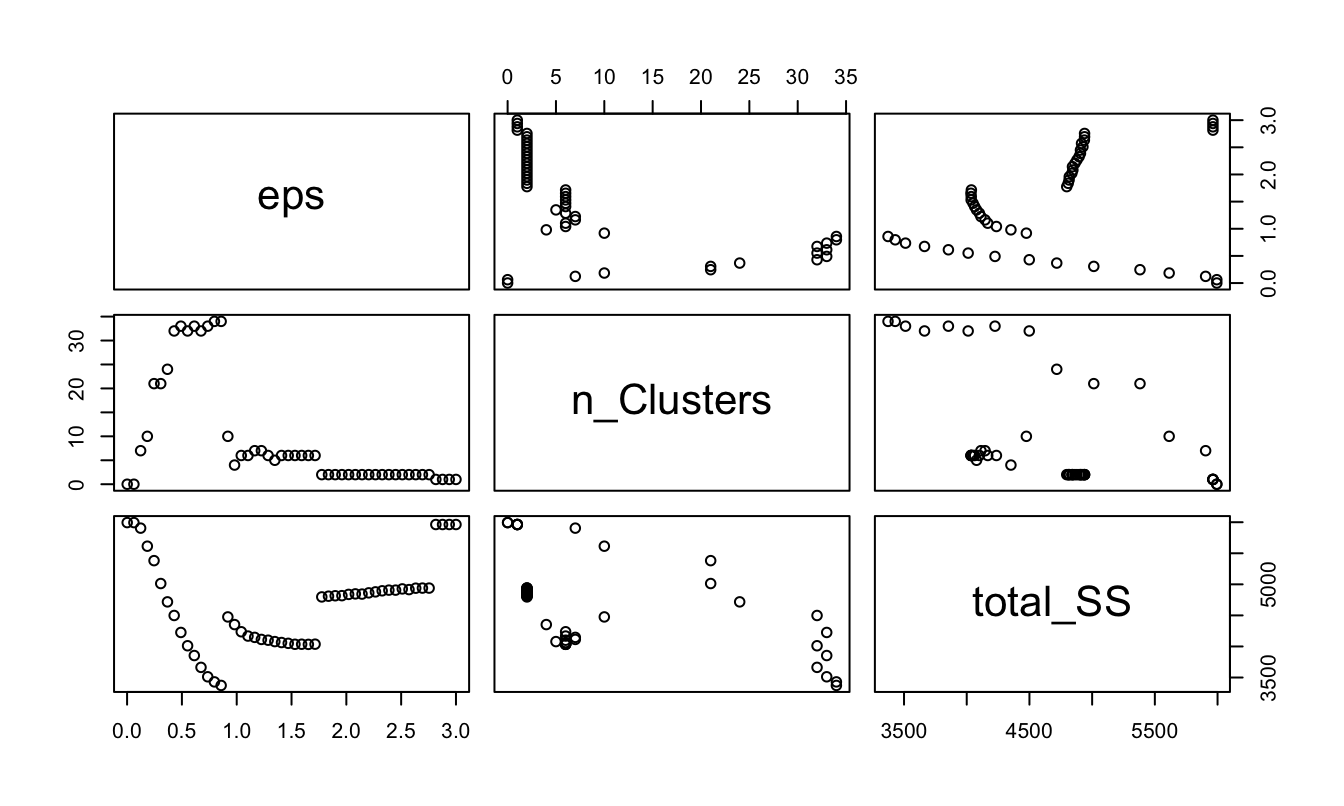
## NULL
El resultado que minimiza la suma de las distancias kNN corresponde a un 0.8578571. Nota que en este caso esto implica 34 clústeres.
El valor óptimo del parámetro eps (\(\epsilon\)) se puede extraer de la siguiente manera:
## [1] 0.85785719.3.2 Detección de anomaías con DBSCAN en R
Ya hemos construido los clústeres, ahora podemos calcular la membrecía de cada individuo. Recuerda que aquellos individuos que no se asignen a un clúster se entenderán como anomalías.
La partición de los datos se puede realizar empleando la función dbscan() del paquete dbscan (Hahsler et al., 2019). La función típicamente incluye los siguientes argumentos:
donde:
x: los datos estandarizados o una matriz de proximidad73.
eps: el parámetro (\(\epsilon\)) que representa el radio máximo del vecindario.
minPts: el número mínimo de individuos (incluyendo al mismo individuo) requeridos en el vecindario \(\epsilon\) (\(\epsilon\)-neighborhhood) para ser considerado como un punto central (core point).
En nuestro caso, primero debemos estandarizar los datos. Estandaricemos los datos empleando la función scale() de la base de R.
Ahora procedamos a particionar las observaciones con el siguiente código:
# Instalar el paquete si no se tiene
# install.packages("dbscan")
# Cargar el paquete
library("dbscan")
# DBSCAN
res_DBSCAN <- dbscan::dbscan(x = german_cuanti_est , eps = eps_opt,
minPts = 5)Las membrecías a los clústeres se pueden encontrar fácilmente con el siguiente código:
## [1] 1 2 0 0 0 0##
## 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
## 273 62 32 32 45 43 11 9 71 7 15 99 28 16 37 32 12 6 7 7
## 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
## 22 6 10 8 15 6 23 6 14 5 6 15 9 6 5Nota que en nuestro caso tenemos 3, 4, 5, 6, 18, 19, 20, 21, 22, 23, 28, 30, 31, 37, 43, 45, 49, 52, 57, 58, 64, 66, 73, 74, 79, 81, 88, 96, 97, 100, 106, 107, 111, 113, 117, 120, 132, 135, 137, 138, 139, 147, 157, 160, 161, 164, 171, 176, 181, 187, 188, 191, 197, 198, 205, 206, 207, 210, 211, 213, 216, 227, 228, 235, 237, 238, 240, 242, 243, 247, 251, 256, 260, 263, 264, 265, 269, 273, 275, 286, 287, 292, 293, 295, 301, 305, 317, 331, 334, 335, 341, 343, 345, 349, 350, 367, 373, 374, 375, 379, 382, 396, 398, 399, 403, 410, 412, 414, 416, 417, 418, 423, 426, 430, 431, 432, 433, 450, 451, 457, 466, 468, 470, 492, 493, 495, 497, 500, 508, 510, 518, 521, 523, 526, 528, 530, 531, 537, 540, 544, 548, 550, 553, 557, 564, 569, 581, 582, 587, 590, 591, 598, 601, 607, 612, 616, 617, 618, 630, 636, 638, 640, 651, 654, 658, 660, 669, 671, 673, 681, 684, 685, 686, 690, 694, 702, 705, 710, 715, 716, 717, 722, 724, 725, 727, 729, 732, 735, 737, 738, 739, 745, 746, 749, 751, 757, 758, 761, 764, 766, 769, 770, 772, 775, 785, 788, 792, 793, 797, 802, 806, 807, 808, 809, 812, 813, 816, 817, 818, 819, 823, 827, 828, 829, 830, 833, 838, 845, 847, 852, 855, 864, 869, 871, 872, 875, 880, 881, 882, 885, 887, 888, 890, 891, 896, 902, 903, 906, 909, 916, 918, 922, 924, 925, 928, 933, 940, 941, 942, 944, 946, 949, 951, 954, 958, 962, 970, 972, 976, 977, 981, 984, 991 observaciones que no han sido clasificadas. Es decir, que fueron asignadas al clúster 0.
Ahora extraigamos el número de los individuos que se pudieron agrupar. Esto lo podemos hacer con el siguiente código:
# Crear objeto con el índice de las observaciones (número de la observación) que son outliers.
DBSCAN_anomal <- as.data.frame(res_DBSCAN$cluster) %>%
mutate(ID = row_number()) %>%
rename(Cluster = `res_DBSCAN$cluster`) %>%
filter(Cluster == 0) %>%
dplyr::select(ID)
dim(DBSCAN_anomal)## [1] 273 1## ID
## 1 3
## 2 4
## 3 5
## 4 6
## 5 18En el objeto DBSCAN_anomal tenemos el índice (número) de las 3, 4, 5, 6, 18, 19, 20, 21, 22, 23, 28, 30, 31, 37, 43, 45, 49, 52, 57, 58, 64, 66, 73, 74, 79, 81, 88, 96, 97, 100, 106, 107, 111, 113, 117, 120, 132, 135, 137, 138, 139, 147, 157, 160, 161, 164, 171, 176, 181, 187, 188, 191, 197, 198, 205, 206, 207, 210, 211, 213, 216, 227, 228, 235, 237, 238, 240, 242, 243, 247, 251, 256, 260, 263, 264, 265, 269, 273, 275, 286, 287, 292, 293, 295, 301, 305, 317, 331, 334, 335, 341, 343, 345, 349, 350, 367, 373, 374, 375, 379, 382, 396, 398, 399, 403, 410, 412, 414, 416, 417, 418, 423, 426, 430, 431, 432, 433, 450, 451, 457, 466, 468, 470, 492, 493, 495, 497, 500, 508, 510, 518, 521, 523, 526, 528, 530, 531, 537, 540, 544, 548, 550, 553, 557, 564, 569, 581, 582, 587, 590, 591, 598, 601, 607, 612, 616, 617, 618, 630, 636, 638, 640, 651, 654, 658, 660, 669, 671, 673, 681, 684, 685, 686, 690, 694, 702, 705, 710, 715, 716, 717, 722, 724, 725, 727, 729, 732, 735, 737, 738, 739, 745, 746, 749, 751, 757, 758, 761, 764, 766, 769, 770, 772, 775, 785, 788, 792, 793, 797, 802, 806, 807, 808, 809, 812, 813, 816, 817, 818, 819, 823, 827, 828, 829, 830, 833, 838, 845, 847, 852, 855, 864, 869, 871, 872, 875, 880, 881, 882, 885, 887, 888, 890, 891, 896, 902, 903, 906, 909, 916, 918, 922, 924, 925, 928, 933, 940, 941, 942, 944, 946, 949, 951, 954, 958, 962, 970, 972, 976, 977, 981, 984, 991 observaciones que no se pudieron agrupar. Estas observaciones serán consideradas como anomalías grupales locales.
9.4 Comentarios finales
En este capítulo hemos estudiado cómo emplear un método de clústering particionado basado en la densidad de los datos como DBSCAN para detectar anomalías locales y multivariadas. Es importante mencionar que los resultados de este algoritmo son muy sensibles a la escogencia de del parámetro eps. Por esta razón, es importante tener una estrategia para fijar, a partir de los datos, este parámetro.
Finalmente, es importante recordar que el algoritmo DBSCAN es una herramienta más para hacer la tarea de detectar anomalías que debes tener en tu caja de herramientas. Como las otras herramientas que hemos estudiado, DBSCAN no es una solución mágica que funcione en todos los casos, pero tiene algunas ventajas sobre otros algoritmos de agrupamiento.
Por ejemplo, DBSCAN no requiere que especifiques el número de vecinos cercanos como si se requiere cuando se emplea la distancia kNN y LOF. Esto puede ser una gran ventaja, ya que a menudo es difícil saber cuántos vecinos debemos emplear.
En el siguiente capítulo continuaremos nuestro análisis de algoritmos para detectar anomalías con modelos de aprendizaje de máquina. Estudiaremos una filosofía totalmente diferente.
En este capítulo hemos estudiado cómo emplear un método de clústering particionado basado en la densidad de los datos como DBSCAN para detectar anomalías locales y multivariadas. Es importante mencionar que los resultados de este algoritmo son muy sensibles a la escogencia de del parámetro eps. Por esta razón, es importante tener una estrategia para fijar, a partir de los datos, este parámetro.
Finalmente, es importante recordar que el algoritmo DBSCAN es una herramienta más para hacer la tarea de detectar anomalías que debes tener en tu caja de herramientas. Como las otras herramientas que hemos estudiado, DBSCAN no es una solución mágica que funcione en todos los casos, pero tiene algunas ventajas sobre otros algoritmos de agrupamiento.
Por ejemplo, DBSCAN no requiere que especifiques el número de vecinos cercanos como si se requiere cuando se emplea la distancia kNN y LOF. Esto puede ser una gran ventaja, ya que a menudo es difícil saber cuántos vecinos debemos emplear.
En el Capítulo 10 estudiaremos un modelo de ML que sigue una filosofía totalmente diferente: el modelo de Isolation Forest.