3 Pruebas estadísticas para encontrar outliers

3.1 Introducción

La detección de anomalías es una tarea recurrente en el trabajo de un científico de datos, ya sea que se estén detectando outliers como parte del proceso de análisis exploratorio de datos (EDA por sus siglas en inglés) o con la finalidad de responder directamente a una pregunta de negocio.

En el Capítulo 2 discutimos que típicamente un análisis estadístico de datos inicia por el proceso del EDA y cómo la detección de outliers era importante en ese proceso³⁴. Recordemos que el EDA es el proceso de examinar y analizar conjuntos de datos para comprender sus características, patrones y tendencias. El EDA es un paso importante en el business analytics, ya que ayuda a los científicos de datos a:

Obtener una comprensión general de los datos permitiendo a los científicos de datos familiarizarse con la estructura, el contenido y las características de los datos.
Identificar patrones y tendencias evidenciando patrones, tendencias y relaciones ocultas en los datos que podrían ser útiles para la construcción de modelos o la toma de decisiones.
Detectar anomalías y errores en los datos identificando valores atípicos, errores y problemas de calidad de los datos que podrían afectar los resultados del análisis.

Por otro lado, en el mundo del business analytics existe un proceso conocido como Extracción, Transformación y Targa (ETL por el término en inglés Extract-Transform-Load) en el que también las técnicas para encontrar anomalías son importantes. El ETL implica el acopio de los datos de diversas fuentes, su limpieza y preparación para su análisis posterior³⁵. Los tres pasos principales del proceso ETL son:

Extracción: Recuperar datos de sistemas de origen, como bases de datos, archivos o APIs.
Transformación: Limpiar, formatear y transformar los datos para que sean consistentes y adecuados para el análisis. Esto puede incluir “eliminar valores atípicos”, corregir errores, estandarizar los formatos y agregar o calcular nuevas variables.
Carga: Transferir los datos transformados en un almacén de datos (bodega de datos o Data Warehouse) o entorno de análisis para su posterior uso.

El ETL y EDA son procesos complementarios en el trabajo de un científico de datos, si bien tienen un foco diferente en el proceso de preparar los datos. El ETL concentra su atención en la limpieza y transformación de datos a gran escala para que sean consistentes y adecuados para el almacenamiento y análisis, y el EDA en la exploración y comprensión de datos preparados para identificar patrones, tendencias y anomalías. Ambos procesos tienen en común la labor de limpiar los datos, si bien el foco de la limpieza no es el mismo. En el ETL, la limpieza de datos se centra en garantizar que los datos sean consistentes, completos y precisos antes de cargarlos en un Data Warehouse o entorno de análisis. El ETL debería garantizar que los datos sean confiables y adecuados para su uso en análisis posteriores. Por otro lado, en el EDA, la limpieza de datos se centra en identificar datos atípicos que podrían afectar los resultados del análisis exploratorio. Esto ayuda a garantizar que la información obtenida del EDA sea precisa y confiable para el modelado y la posterior toma de decisiones.

El ETL y EDA son procesos complementarios en la ciencia de datos que están relacionados (Ver Figura 3.1). La limpieza de datos es una parte crucial de ambos procesos, asegurando que los datos sean confiables, consistentes y adecuados para su uso en análisis y modelado. En ambos casos, la detección de anomalías hace parte del proceso de limpieza de los datos.

Figura 3.1: La detección de anomalías en los procesos de ETL, EDA y modelado en el mundo del business analytics

Fuente: elaboración propia.

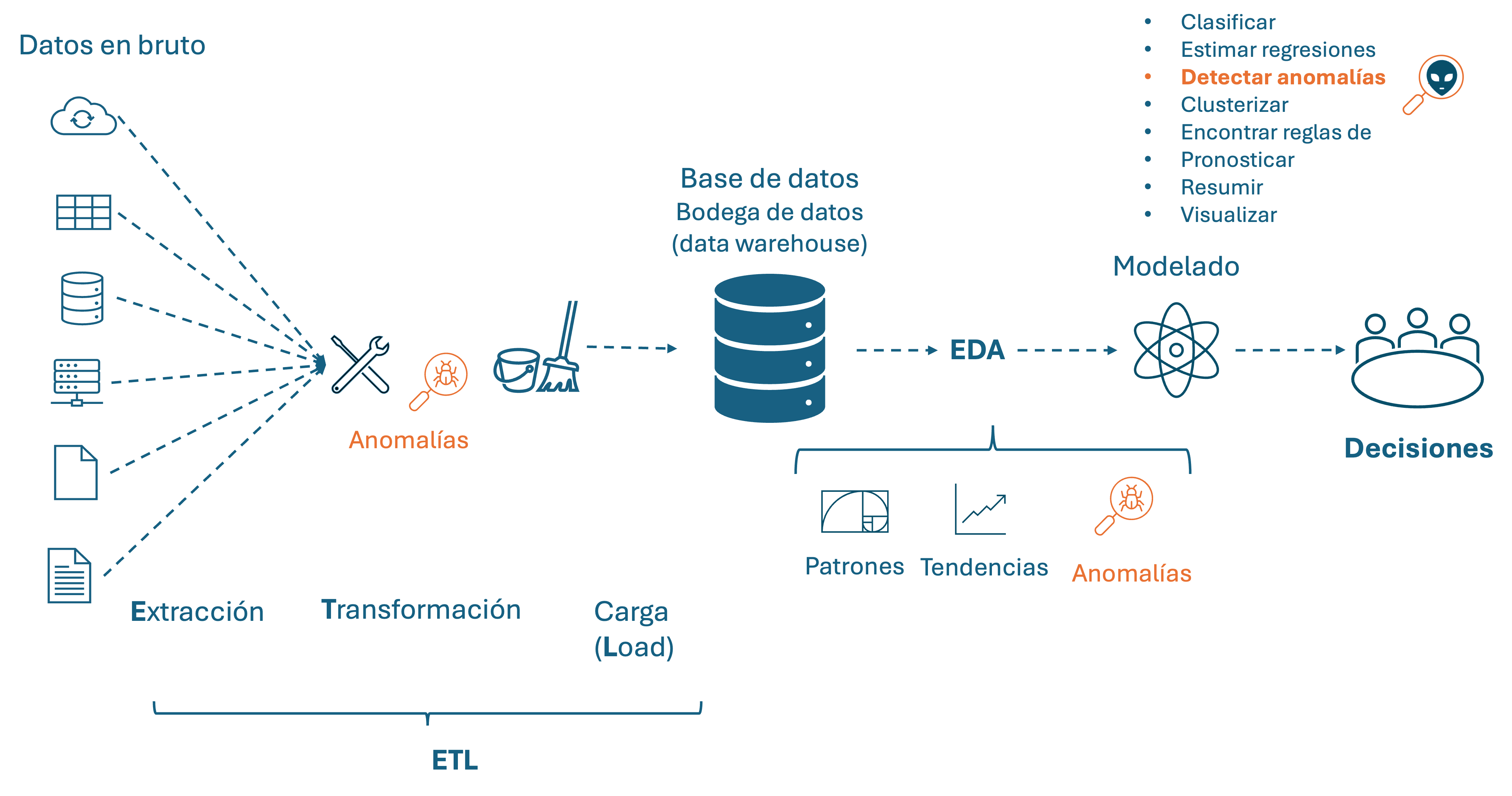
Como se ha mencionado, la limpieza de una base de datos en los proyectos de analítica es esencial para garantizar la calidad y confiabilidad de los resultados obtenidos. En este contexto, las técnicas de detección de outliers desempeñan un papel fundamental en la identificación de errores de digitación, errores de medición o individuos con comportamientos anormales, de tal manera que será necesario tomar alguna acción para garantizar que los modelos estimados o entrenados brinden los insights correctos para la toma de decisiones.

En la limpieza de datos, si se encuentran anomalías, pueden ser fruto de un error de registro o de medición, la decisión puede ser capturar de nuevo la medición o descartar la observación si no es posible volverla a medir o reemplazar el correspondiente valor atípico por un NA. Típicamente esto debería hacer parte del proceso de ETL. Por otro lado, la observación anómala fruto de un comportamiento diferente de un individuo debería mantenerse en la muestra y, de ser necesario, modelar ese comportamiento atípico para comprender su impacto y tomar decisiones informadas.

Finalmente, es importante recalcar que la detección de anomalías puede ser por sí misma el objetivo del ejercicio de modelado de datos del científico de datos (Ver parte superior derecha de la Figura 3.1). Típicamente las técnicas de detección de anomalías que se emplean en el ETL y EDA corresponden más a técnicas estadísticas para detectar outliers (anomalías puntuales o globales) univariados. Esto garantiza una base de datos confiable para el posterior modelado y la solución de las preguntas de negocio planteadas. Por otro lado, cuando se requiere responder preguntas de negocio que implican la tarea de detección de anomalías es más común que se empleen técnicas de detección de anomalías multivariadas, contextuales (locales) o colectivas; en especial técnicas de origen en el aprendizaje de máquina.

Como lo estudiamos en el Capítulo 1, existen diferentes tipos de anomalías y, por tanto, diferentes tipos de aproximarnos a su detección. En el Capítulo 2 estudiamos el uso de la aproximación gráfica (histogramas y boxplots) y el uso de métricas (percentiles, z-score, rango intercuartílico, método de Hampel y métricas que emplean estimadores robustos de varianza y media). Si bien estas dos aproximaciones nos dan una idea de cuáles observaciones son inusuales, no permiten realizar inferencia estadística. En otras palabras, no nos permiten tener una confianza del 95% o 99% de nuestras decisiones.

En este capítulo estudiaremos cuatro diferentes pruebas estadísticas que permiten hacer inferencia estadística sobre la presencia o no de datos anómalos en una variable; es decir, la existencia de outliers univariados. Estas cuatro pruebas hacen parte de las técnicas estadísticas formales para la identificación de valores atípicos. Las cuatro implican el cálculo de un estadístico de prueba y su comparación contra valores críticos, que depende del tamaño de la muestra, de supuestos sobre el comportamiento de la variable y del nivel de confianza o insignificancia deseado.

Las pruebas que estudiaremos aquí suponen que los datos de la variable bajo estudio, sin tener en cuenta los valores atípicos, provienen de un proceso generador de datos (DGP por sus siglas en inglés) que sigue una distribución aproximadamente normal. Por eso es común que antes de emplear estas pruebas, el primer paso sea comprobar la normalidad de los datos utilizando análisis visual y recurriendo a pruebas de normalidad formales. No obstante, aquí aparece un problema práctico delicado, pues la existencia de valores atípicos puede hacer que las pruebas tradicionales de normalidad pierdan su poder. Es decir, en presencia de valores atípicos, las pruebas formales de normalidad tienden a rechazar la hipótesis nula de normalidad cuando en realidad los datos sí provienen de un DGP que sigue una distribución normal. Es por eso que es más común la inspección gráfica del supuesto de normalidad que el uso de las pruebas formales de normalidad.

3.2 Pruebas

En esta sección discutiremos cuatro pruebas estadísticas para determinar si existe o no outliers en una muestra de una variable. Para esta sección emplearemos la siguiente notación:

\(X\): variable cuantitativa para la que se quiere probar la presencia o no de datos atípicos.
\(X_i\): la \(i\)-ésima observación muestral de la variable \(X\). Además, tendremos \(i=1, 2, \dots , n\).
\(\bar{X}\): media muestral para todas las observaciones de la variable \(X\).
\(\bar{X}_k\): media de la muestra que queda tras remover las \(k\) observaciones más extremas (o todas las \(k\) más pequeñas o todas las \(k\) más grandes) de la variable \(X\).
\(\min(X)\): el valor mínimo observado para la muestra de la variable \(X\).
\(\max(X)\): el valor máximo observado para la muestra de la variable \(X\).
\(s\): desviación estándar para la muestra de la variable \(X\).
\(X_{(i)}\): la \(i\)-esima observación tras ordenar de menor a mayor los datos. Es decir, \(X_{(1)} < X_{(2)} < X_{(3)} < \dots X_{(n-1)}<X_{(n-1)}\). Además, \(X_{(1)} =\min(X)\) y \(X_{(n)} =\max(X)\).

3.2.1 Prueba de Grubbs

La prueba propuesta por Grubbs (1969) es de las pruebas más empleadas para detectar un único outlier en una variable cuantitativa (\(X\)). Esta prueba permite probar las siguientes hipótesis nula (\(H_0\)) y alterna (\(H_A\)):

\(H_0\): La muestra proviene de una distribución normal sin outliers.
\(H_A\): Hay un outlier en la muestra.

Grubbs (1969) demostró que para probar esta hipótesis nula se puede emplear el siguiente estadístico de prueba: \[\begin{equation} G = \frac{\max{|X_{i} - \bar{X}|}} {s} \tag{3.1} \end{equation}\]

Grubbs (1969) además demostró que \(G\) sigue una distribución t de Student con \(n-2\) grados de libertad. Nota que la anterior prueba corresponde a una prueba de dos colas al estar buscando valores atípicos tanto en la cola inferior como en la superior de la distribución. También es posible probar si el valor mínimo (máximo) es un valor atípico. En este caso la hipótesis nula y alterna son:

\(H_0\): El valor mínimo (máximo) no es un outlier.
\(H_A\): El valor mínimo (máximo) es un outlier.

En el caso de probar si el valor mínimo es un valor atípico, el estadístico de prueba será: \[\begin{equation} G = \frac{\bar{X} - \min(X)} {s} \tag{3.2} \end{equation}\] Y para el valor máximo tendremos: \[\begin{equation} G = \frac{\max(X) - \bar{X}} {s} \tag{3.3} \end{equation}\] En estos dos últimos casos, los estadísticos de prueba siguen la misma distribución; la única diferencia es que se trata de pruebas de una sola cola.

La prueba de Grubbs tiene un supuesto muy fuerte: se supone que la muestra fue generada a partir de una distribución normal univariada. Este test funciona relativamente bien con muestras grandes, aunque el supuesto no se cumpla, pero puede ser muy sensible a la violación del supuesto de normalidad en muestras pequeñas. Otra desventaja de esta prueba es que está diseñada únicamente para detectar un outlier. Si se intuye (con el análisis gráfico o con métricas como las estudiadas en el Capítulo 2) la existencia de más de un dato atípico, esta prueba no es una buena opción.

3.2.2 Prueba de Dixon

Dixon (1950) propuso otra prueba conocida como la prueba de Dixon, la Q de Dixon (Dixon’s Q test) o prueba Q. Esta prueba permite probar las mismas tres \(H_0\) que la de Grubbs. Para el caso de la prueba de una cola cuya \(H_0\) es que el valor mínimo no es un outlier, el estadístico de prueba propuesto por Dixon (1950) corresponde a: \[\begin{equation} Q_{\min} = \frac{X_{(2)}-\min(X)} {\max(X)-\min(X)} \tag{3.4} \end{equation}\]

Y para el caso de que la \(H_0\) sea que el valor máximo no es un outlier, el estadístico de prueba propuestos por Dixon (1950) corresponde a: \[\begin{equation} Q_{\max} = \frac{\max(X) - X_{(n-1)}} {\max(X)-\min(X)} \tag{3.5} \end{equation}\] Dixon (1950) demostró que estos estadísticos siguen una distribución especial que depende del tamaño de la muestra y del nivel de significancia. Posteriormente, Dixon (1951) provee unas tablas para tomar la decisión de esta prueba. Más adelante, Rorabacher (1991) propone una forma alternativa de encontrar los valores críticos para tomar la decisión de la prueba de Dixon. En todo caso, y al igual que la prueba de Grubbs, la prueba depende del supuesto de que la muestra proviene de una distribución normal univariada. Esta prueba no funciona bien (ni en muestras grandes) cuando se viola el supuesto de normalidad. Además, está documentado que la prueba de Dixon es útil principalmente para muestras pequeñas (\(3 \leqslant n \leqslant30\)).

3.2.3 Prueba de Rosner

La prueba de Rosner (Rosner, 1975) se emplea para detectar outliers en un conjunto de datos univariados, pero a diferencia de las pruebas de Grubbs y Dixon, se enfoca en detectar múltiples outliers.

Esta prueba tiene como hipótesis:

\(H_0\): La muestra proviene de una distribución normal sin outliers.
\(H_A\): Hay \(k\) outliers en la muestra.

La estadística de prueba para la prueba de Rosner se basa en el cálculo de las distancias máximas a la media estudentizada, que se obtienen al dividir la diferencia de cada valor extremo y la media por la desviación estándar ajustada (Ver Rosner (1975) para una descripción en detalle de esta prueba).

El estadístico de Rosner, al igual que el de Dixon, no sigue una distribución convencional y depende del número de outliers a probar (\(k\)). La decisión se toma comparando el estadístico calculado con los valores provistos por Rosner (1975) para diferentes niveles de significancia y tamaños de muestra.

Al igual que las pruebas anteriores, esta prueba tiene como supuesto que la muestra proviene de una distribución normal univariada. Es sensible a violaciones de la normalidad y al tamaño de la muestra. Como se mencionó anteriormente, la gran ventaja de esta prueba es que se puede emplear para identificar \(k\) valores atípicos. A diferencia de las dos pruebas anteriores (Grubbs y Dixon), para las cuales se debe recurrir a realizar el proceso de forma iterativa para verificar más de un posible atípico, si bien este procedimiento iterativo no es recomendable, en especial para la prueba de Dixon. Comúnmente, esta prueba se emplea cuando el tamaño de la muestra es grande (\(n \geqslant 20\)).

3.3 Empleando R para realizar pruebas de la presencia de outliers univariados

Empecemos por cargar los mismos datos del Capítulo 2. Recuerda que la base de datos correspondía a un banco comercial alemán que contenía datos de clientes a los que se les ha otorgado un crédito y se han calificado como buenos o malos deudores. Los datos provienen de Hofmann (1994) y se encuentran en el archivo datos_credito.RData que se puede descargar de la página web del libro (https://www.icesi.edu.co/editorial/deteccion-anomalias). La descripción de las variables se encuentra en la Sección 2.4.

Carguemos los datos:

load("./datos/datos_credito.RData")

Los datos están cargados en el objeto de clase data.frame que denominamos german. Ese objeto tiene 14 variables y 1000 clientes. Miremos rápidamente los datos cargados empleando la función glimpse() del paquete dplyr (Wickham et al., 2021).

library(dplyr)
glimpse(german)

## Rows: 1,000
## Columns: 14
## $ cuenta.corriente      <fct> less than 0 DM, 0 or less than 200 DM, no checki…
## $ historial.crediticio  <fct> critical account/ other credits existing (not at…
## $ proposito             <fct> radio/television, radio/television, education, f…
## $ monto.credito         <int> 1169, 5951, 2096, 7882, 4870, 9055, 2835, 6948, …
## $ cuenta.ahorros        <fct> unknown/ no savings account, less than 100 DM, l…
## $ porcentaje.disponible <int> 4, 2, 2, 2, 3, 2, 3, 2, 2, 4, 3, 3, 1, 4, 2, 4, …
## $ estadocivil.sexo      <fct> male : single, female : divorced/separated/marri…
## $ residente             <int> 4, 2, 3, 4, 4, 4, 4, 2, 4, 2, 1, 4, 1, 4, 4, 2, …
## $ edad                  <int> 67, 22, 49, 45, 53, 35, 53, 35, 61, 28, 25, 24, …
## $ propiedad.hogar       <fct> own, own, own, for free, for free, for free, own…
## $ numero.creditos       <int> 2, 1, 1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, …
## $ ocupacion             <fct> skilled employee / official, skilled employee / …
## $ dependientes          <int> 1, 1, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
## $ trabajador.extranjero <fct> yes, yes, yes, yes, yes, yes, yes, yes, yes, yes…

Recuerda que contamos con 6 variables cuantitativas: monto.credito, porcentaje.disponible, residente, edad, numero.creditos, dependientes. En el Capítulo 2 concentramos nuestro análisis de datos atípicos en la variable monto.credito. Y las Figuras 2.4, 2.5 y 2.6 nos mostraban que la distribución de los datos es asimétrica. Por eso sería muy difícil asumir que los datos siguen una distribución normal como lo requieren las pruebas estudiadas anteriormente.

Indaguemos si podemos asumir que alguna de las otras 5 variables cuantitativas en nuestra base de datos sigue una distribución normal.

3.3.1 Verificación gráfica del cumplimiento del supuesto de normalidad

Una forma rápida de verificar si una muestra de datos univariados (una variable) sigue una distribución normal es empleando un diagrama qq o también conocido como un qq plot (Quantile-Quantile Plot). El diagrama qq permite comparar la distribución de un conjunto de datos con una distribución de referencia, como por ejemplo la distribución normal. En otras palabras, permite visualizar si los datos siguen una distribución específica o si se alejan significativamente de ella.

Para construir un diagrama qq, se ordenan los datos de menor a mayor y se calculan sus respectivos cuantiles (cuantiles observados). Por otro lado, se calculan los cuantiles de la distribución de referencia (por ejemplo, normal). El diagrama qq implica construir un diagrama de dispersión que tiene en el eje horizontal los cuantiles teóricos (los de la distribución de referencia) y en el eje vertical los cuantiles de la distribución de referencia.

Si los puntos del diagrama qq se encuentran aproximadamente sobre una línea recta, significa que la distribución de los datos es similar a la distribución de referencia. En cambio, si los puntos se alejan significativamente de la línea recta, indica que la distribución de los datos se diferencia de la distribución de referencia. Si se observa una curva hacia arriba, esto implica que los datos observados tienen una cola superior más pesada que la distribución de referencia. Y si se observa una curva hacia abajo, los datos tienen una cola izquierda (inferior) más pesada que la distribución de referencia. Es importante anotar que la presencia de outliers puede afectar significativamente la forma del diagrama.

El diagrama qq se puede construir en R de muchas maneras. Por ejemplo, se puede emplear la función qqplot() de la base de R. También se puede emplear la función qqPlot() del paquete car (Fox & Weisberg, 2019). ¡Inténtalo! En este libro emplearemos el paquete ggplot2 (Wickham, 2016) para construir el diagrama qq. En este paquete se cuenta con las capas stat_qq() y stat_qq_line(). La primera de estas capas grafica los puntos correspondientes al diagrama qq y la segunda traza la correspondiente línea recta. Para emplear estas dos capas, necesitaríamos emplear en la capa de estética el argumento sample que mapeará los datos de la variable observada al diagrama qq. Por ejemplo, para la variable edad el correspondiente diagrama qq (Ver Figura 3.2) se puede construir con el siguiente código:

library(ggplot2)

german %>% 
 ggplot( aes(sample = edad))+ 
  stat_qq(color = "steelblue", alpha = 0.5) + 
  stat_qq_line(color = "steelblue") +  
  xlab("Cuantiles teóricos") +
  ylab("Cuantiles observados") +
  theme_minimal()

Figura 3.2: Diagrama qq para la variable edad

Fuente: elaboración propia.

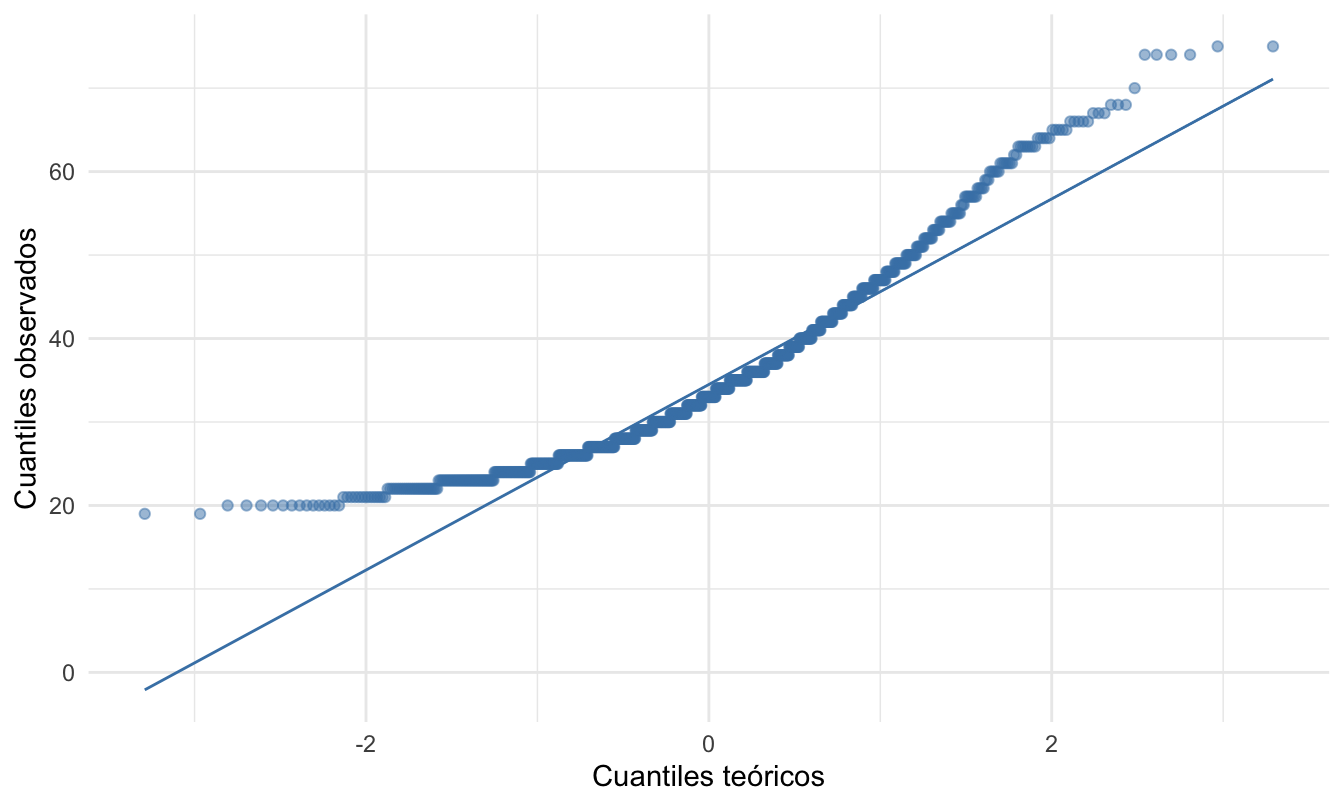
Como se puede evidenciar en la Figura 3.2, las observaciones se desvían de la línea de referencia formando una curva hacia arriba. Esto es reflejo de que los datos observados tienen una cola superior más pesada que la distribución de referencia. Puedes constatar esto construyendo el respectivo histograma y boxplot. Es decir, la variable no evidencia seguir una distribución normal.

Te podrás estar preguntando qué tan alejados de la línea de referencia deben estar los puntos para determinar que la variable observada se distancia de la distribución normal. Para resolver esta pregunta, podemos construir intervalos de confianza para la línea de referencia, de tal manera que, si los puntos caen en el intervalo, podemos concluir que los datos no se distancian de la distribución de referencia. Esto lo podemos hacer en R empleando el paquete qqplotr (Almeida et al., 2018) . Este paquete provee una capa adicional que construye el intervalo de confianza para la línea de referencia, esto lo logramos con la función stat_qq_band(). Para poder emplear esta capa se debe reemplazar la capa stat_qq() por stat_qq_point(). El código para generar la Figura 3.3 que muestra el diagrama qq con sus respectivas bandas es el siguiente:

# install.packages("qqplotr")
library(qqplotr)

german %>% 
 ggplot( aes(sample = edad))+ 
  stat_qq_band() + 
  stat_qq_point(color = "steelblue", alpha = 0.5)    +           
  stat_qq_line(color = "steelblue") +  
  xlab("Cuantiles teóricos") +
  ylab("Cuantiles observados") +
  theme_minimal()

Figura 3.3: Diagrama qq con su intervalo de confianza para la variable edad

Fuente: elaboración propia.

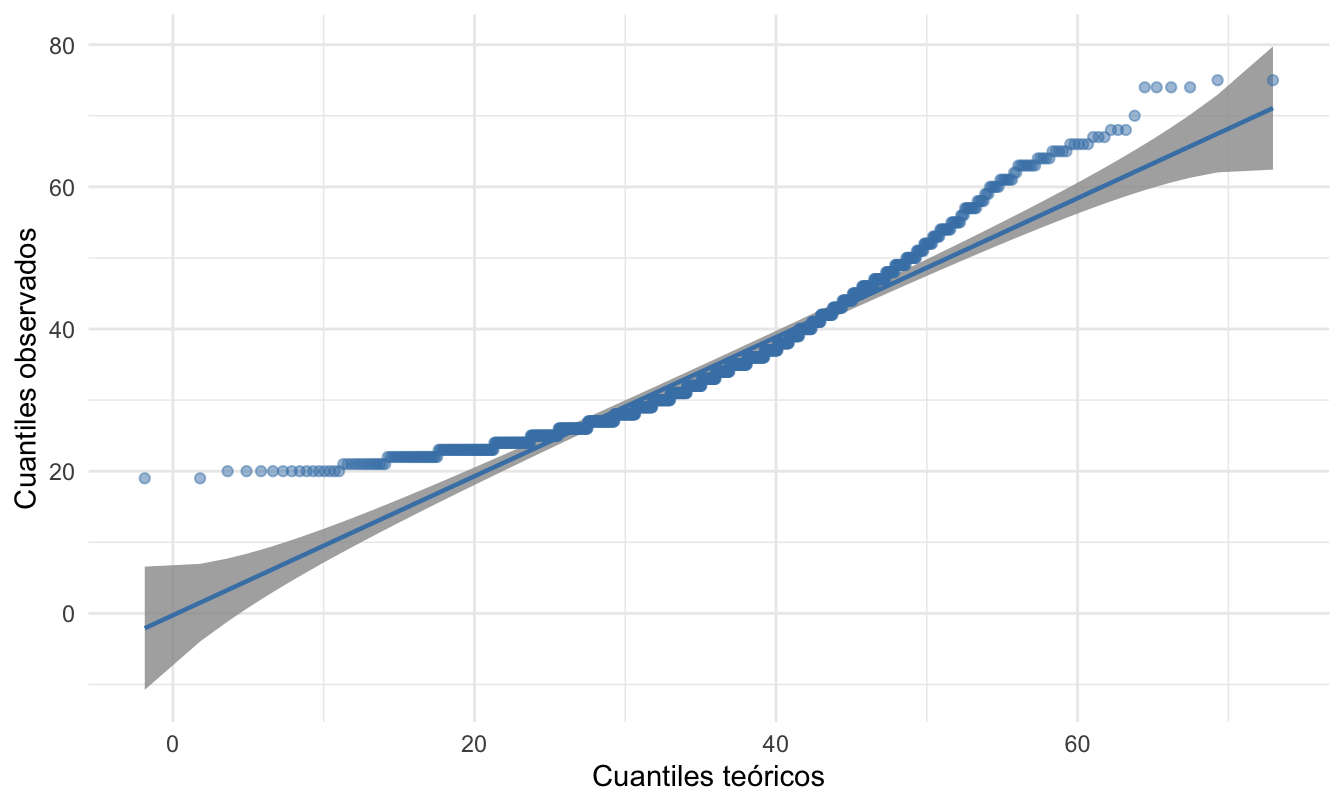
Con las bandas, la decisión es mucho más sencilla. ¡Comprueba que las variables porcentaje.disponible, residente, numero.creditos y dependientes no provienen de una distribución normal! Esto implica que las técnicas estudiadas en este capítulo no deberíamos emplearlas.

Para continuar nuestra ilustración de cómo emplear estas pruebas para detectar outliers, creemos dos series. Una variable W generada a partir de una distribución normal con un solo outlier y una variable Z con 7 outliers, 3 en la parte inferior y 4 en la parte superior.

Con el siguiente código podemos generar estas dos variables:

set.seed(1234)
datos_prueba <- data.frame(W=c(rnorm(999), 6), 
                           Z=c(rnorm(993), -9, -6, -10, 10, 8, 6, 7.5))

Constatemos que las dos series generadas siguen una distribución normal. ¡Intenta reproducir los dos paneles de la Figura 3.4!

Figura 3.4: Diagrama qq para las dos series generadas aleatoriamente

Fuente: elaboración propia.

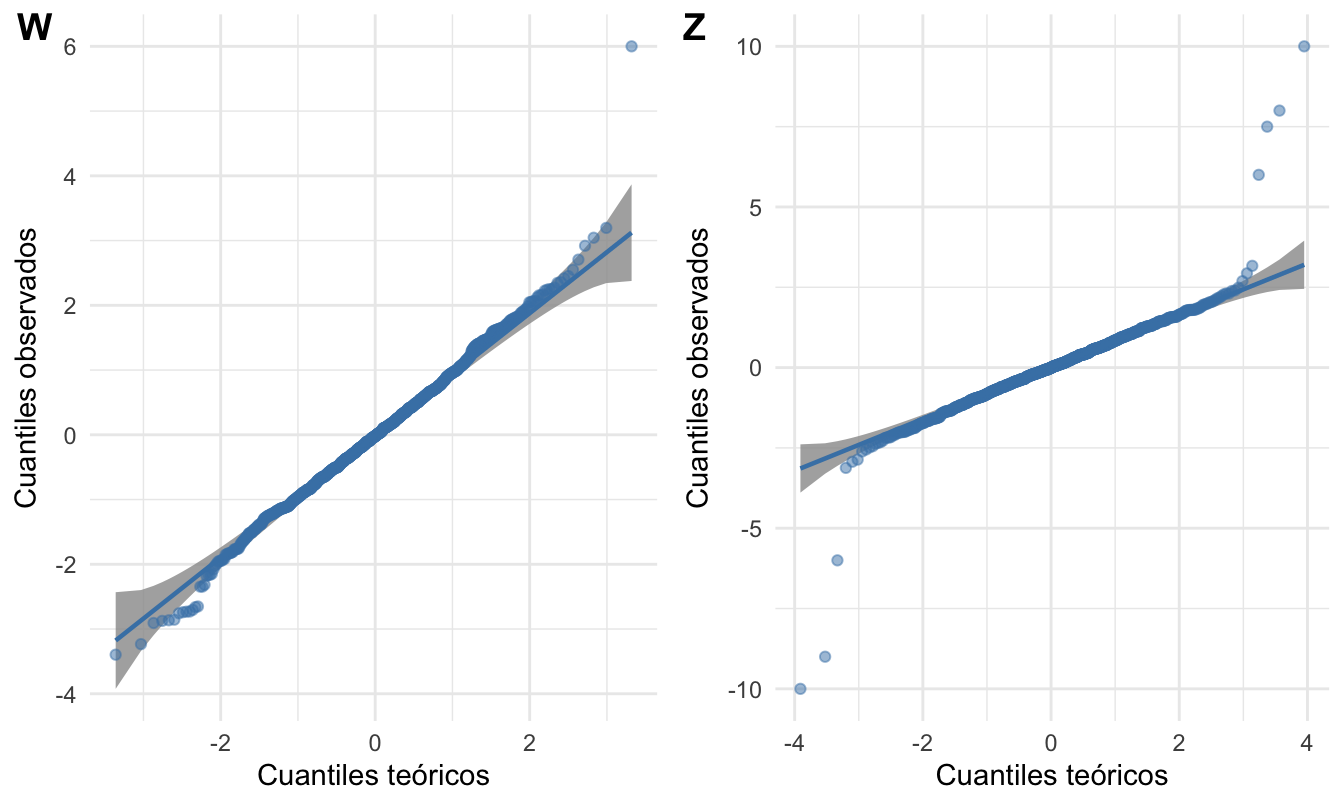
Como se puede observar en la Figura 3.4, para ambas series, la mayoría de las observaciones no se desvían de la línea de referencia (con excepción de los datos atípicos). Esto permite concluir que los datos provienen de una distribución normal. Naturalmente, en este caso sabemos que ambas variables sí fueron generadas de una distribución normal.

3.3.2 Pruebas en R

Una vez constatado que el supuesto de normalidad es plausible para la muestra, podemos proceder a realizar las pruebas para detectar la presencia de outliers. En esta sección estudiaremos cómo implementar las pruebas de Grubbs, Dixon y Rosner en R.

3.3.3 Prueba de Grubbs

La prueba de Grubbs se puede implementar en R por medio de la función grubbs.test() del paquete outliers (Komsta, 2022). Esta función tiene como argumento x los datos de la variable que deseamos chequear y el otro argumento importante de la función es type que especifica el tipo de prueba que se quiere realizar. Si type = 10 se realizará una prueba para detectar si la muestra contiene un valor atípico. El lado en el que estará el valor atípico es detectado automáticamente. Si type = 11 se comprobará si el valor más bajo y el más alto son dos valores atípicos.

Realicemos la prueba para la variable W que sabemos que solo tiene un valor atípico en la parte superior. En este caso el código será:

# install.packages("outliers")
library(outliers) 
grubbs.test(datos_prueba$W ,  type = 10)

## 
##  Grubbs test for one outlier
## 
## data:  datos_prueba$W
## G = 5.92947, U = 0.96477, p-value = 1.107e-06
## alternative hypothesis: highest value 6 is an outlier

El estadístico de la prueba es 5.9885, con un valor p³⁶ muy pequeño. Por tanto, con un nivel de confianza del 99%, rechazamos la hipótesis de que el valor más alto 6 no es un valor atípico. En otras palabras, con base en esta prueba, concluimos que el valor más alto es un valor atípico.

En este caso, la función detectó automáticamente que se deseaba encontrar si el máximo era un outlier. Si queremos que la función pruebe si el mínimo es un outlier, podemos emplear el argumento opposite = FALSE. Este argumento le dice a la función si deseamos comprobar si el valor con mayor diferencia respecto a la media es outlier (opposite = TRUE) o el lado opuesto.

Por ejemplo, para probar si el mínimo es un outlier el código sería:

grubbs.test(datos_prueba$W,  type = 10, opposite = TRUE)

## 
##  Grubbs test for one outlier
## 
## data:  datos_prueba$W
## G = 3.32506, U = 0.98892, p-value = 0.4288
## alternative hypothesis: lowest value -3.39606353457436 is an outlier

El valor p es mayor que 0.05. Con un nivel de confianza del 95%, no rechazamos la hipótesis nula, la cual plantea que el valor más bajo no es un valor atípico. En otras palabras, no podemos concluir que el valor más bajo sea un valor atípico de acuerdo con el conjunto de datos con el que estamos trabajando.

Finalmente, si queremos detectar si el valor mínimo y máximo son valores atípicos tendríamos el siguiente código:

grubbs.test(datos_prueba$W,  type = 11)

## 
##  Grubbs test for two opposite outliers
## 
## data:  datos_prueba$W
## G = 9.25453, U = 0.95373, p-value < 2.2e-16
## alternative hypothesis: -3.39606353457436 and 6 are outliers

La prueba tiene un valor p aproximadamente de cero. En este caso podemos rechazar la hipótesis nula porque es inferior al nivel de significancia (\(\alpha = 0.01\)), por lo que concluimos que tenemos evidencia suficiente para determinar que los valores mínimo y máximo son valores atípicos (o solo uno de ellos) en la variable W.

3.3.4 Prueba de Dixon

La prueba de Dixon puede ser implementada empleando la función dixon.test.test() del paquete outliers (Komsta, 2022). Esta prueba funciona relativamente bien en muestras pequeñas, por eso la misma función solo permite muestras pequeñas entre 3 y 25 observaciones (\(3 \leqslant n \leqslant25\)). Para seguir con nuestro ejemplo, utilizaremos un subconjunto de los datos simulados que tendrá 24 observaciones y el valor atípico.

datos_test_dixon <- c(datos_prueba$W[1:23], max(datos_prueba$W))

Si queremos probar la \(H_{0}:\) de que el máximo valor no es una atípico, el código será el siguiente:

dixon.test(datos_test_dixon)

## 
##  Dixon test for outliers
## 
## data:  datos_test_dixon
## Q = 0.70238, p-value < 2.2e-16
## alternative hypothesis: highest value 6 is an outlier

La prueba tiene un valor p muy pequeño; dado que este valor es inferior al nivel de significancia, tenemos evidencia suficiente para rechazar la hipótesis nula (con un 99% de confianza) y determinar que el valor máximo es un valor atípico. De la misma manera que la función grubbs.test(), esta función detecta automáticamente dónde está la observación con la mayor dispersión con respecto a la media. Si se desea probar (con estos datos) la \(H_{0}\) de que el mínimo valor no es una atípico, se puede emplear el siguiente código:

dixon.test(datos_test_dixon, opposite = TRUE)

## 
##  Dixon test for outliers
## 
## data:  datos_test_dixon
## Q = 0.39279, p-value = 0.1379
## alternative hypothesis: lowest value -2.34569770262935 is an outlier

Dado el valor p obtenido, y aún empleando un nivel de significancia del 10%, no podemos rechazar la hipótesis nula. La cual implica que el valor más bajo no es un valor atípico. En otras palabras, no podemos concluir que el valor mínimo sea un valor atípico de acuerdo al conjunto de datos con el que estamos trabajando.

3.3.5 Prueba de Rosner

Por otro lado, la prueba de Rosner se emplea cuando el tamaño de la muestra es superior a 20 (\(n \geqslant 20\)). Esta se puede implementar con la función rosnerTest() del paquete EnvStats (Millard, 2013). Esta función requiere los siguientes tres argumentos:

rosnerTest(x, k, alpha)

donde:

x: vector numérico de observaciones.
k: número entero positivo que indica el número de observaciones atípicas sospechosas. El argumento k debe estar comprendido entre 1 y \(n-2\). El valor por defecto es k = 3.
alpha: número que puede tomar valores entre 0 y 1 y que corresponde al error tipo I asociado a la prueba (como predeterminado alpha = 0.05).

Por ejemplo, para la serie Z probemos la existencia de 10 valores atípicos, recuerden que generamos solo 7 outliers. Eso lo podemos realizar con el siguiente código.

#Cargar el paquete
library(EnvStats)
# Realizar la prueba de Rosner
rst <- rosnerTest(datos_prueba$Z, k=10, alpha = 0.01)

print(rst)

## 
## Results of Outlier Test
## -------------------------
## 
## Test Method:                     Rosner's Test for Outliers
## 
## Hypothesized Distribution:       Normal
## 
## Data:                            datos_prueba$Z
## 
## Sample Size:                     1000
## 
## Test Statistics:                 R.1  = 8.385497
##                                  R.2  = 8.650771
##                                  R.3  = 8.132802
##                                  R.4  = 7.435410
##                                  R.5  = 7.175184
##                                  R.6  = 5.920776
##                                  R.7  = 5.993057
##                                  R.8  = 3.218524
##                                  R.9  = 3.209715
##                                  R.10 = 3.031358
## 
## Test Statistic Parameter:        k = 10
## 
## Alternative Hypothesis:          Up to 10 observations are not
##                                  from the same Distribution.
## 
## Type I Error:                    1%
## 
## Number of Outliers Detected:     7
## 
##    i      Mean.i      SD.i      Value Obs.Num    R.i+1 lambda.i+1 Outlier
## 1  0 0.019401810 1.1948490 -10.000000     996 8.385497   4.396763    TRUE
## 2  1 0.029431241 1.1525642  10.000000     997 8.650771   4.396529    TRUE
## 3  2 0.019440691 1.1090200  -9.000000     994 8.132802   4.396295    TRUE
## 4  3 0.028487272 1.0721014   8.000000     998 7.435410   4.396061    TRUE
## 5  4 0.020483745 1.0424145   7.500000    1000 7.175184   4.395826    TRUE
## 6  5 0.012966643 1.0155707  -6.000000     995 5.920776   4.395592    TRUE
## 7  6 0.019015905 0.9979856   6.000000     999 5.993057   4.395357    TRUE
## 8  7 0.012992759 0.9802460   3.167938     816 3.218524   4.395122   FALSE
## 9  8 0.009812371 0.9756012  -3.121590     661 3.209715   4.394886   FALSE
## 10 9 0.012972212 0.9710017  -2.930482     122 3.031358   4.394650   FALSE

Como se puede evidenciar en los resultados, vemos que existen 7 valores atípicos con un nivel de confianza del 99%, observaciones que corresponden a aquellas que generamos.

3.4 Comentarios finales

En este capítulo continuamos el análisis de anomalías univariadas. Incorporamos en nuestra caja de herramientas 3 pruebas estadísticas para detectar la presencia de ouliers (anomalías puntuales). Las pruebas estadísticas permiten una decisión formal sobre la presencia de outliers, pero deben usarse con cautela. Sus resultados dependen de los supuestos de normalidad y del tamaño de muestra, por lo que conviene complementarlas con la validación de los supuestos y cuando sea pertinente con las herramientas gráficas y métricas descriptivas presentadas en el Capítulo 2.

Antes de continuar con el estudio de técnicas para detectar anomalías multivariadas en el Capítulo 4, es importante resaltar que cuando se realiza una prueba de valores atípicos se puede caer en lo que se conoce en la jerga de la literatura de detección de anomalías como enmascaramiento (masking) y swamping³⁷.

Para entender estos dos conceptos reconozcamos que cuando se realiza una prueba de valores atípicos, es necesario elegir un procedimiento basado en el número de valores atípicos (como por ejemplo las pruebas de Grubbs y Dixon) o especificar el número de valores atípicos para una prueba (como la prueba de Rosner). Las pruebas de Grubbs y Dixon solo comprueban un valor atípico. Sin embargo, otros procedimientos, como la prueba de Rosner y la de Tietjen-Moore (Tietjen & Moore, 1972)³⁸, requieren que se especifique el número de valores atípicos. Es difícil hacerlo correctamente. Al fin y al cabo, estamos realizando la prueba para encontrar valores atípicos. El enmascaramiento y el swamping son dos problemas que pueden producirse cuando se especifica un número incorrecto de valores atípicos en un conjunto de datos.

El enmascaramiento se produce cuando se especifican muy pocos valores atípicos. En general, se dice que un valor atípico enmascara un segundo valor atípico, si el segundo valor atípico puede considerarse un valor atípico solo por sí mismo, pero no en presencia del primer valor atípico. Así, tras la eliminación del primer valor atípico, el segundo aparece como tal. Los valores atípicos adicionales que existan pueden afectar a la prueba para que no detecte ningún valor atípico. Por ejemplo, si se especifica un valor atípico cuando hay dos, la prueba puede pasar por alto ambos valores atípicos.

Por el contrario, cuando se especifica un número excesivo de valores atípicos, se produce un efecto swamping. Se dice que un valor atípico “empantana” una segunda observación, si esta última solo puede considerarse un valor atípico en presencia del primero. En este caso, la prueba identifica demasiados puntos de datos como valores atípicos. Por ejemplo, si especifica dos valores atípicos cuando solo hay uno, la prueba podría determinar que hay dos valores atípicos.

Así, cuando estamos empleando técnicas de detección de anomalías, como las pruebas de Grubbs y Dixon, es importante tener en cuenta la posibilidad del masking y swamping.

En el Capítulo 4 continuaremos nuestro estudio de herramientas para la detección de anomalías concentrándonos en técnicas para detectar outliers multivariados. Por ahora recuerda que las anomalías pueden ser de diferentes tipos y por eso es importante que tengamos diversas herramientas para su detección.

Referencias

Almeida, A., Loy, A., & Hofmann, H. (2018). ggplot2 compatible quantile-quantile plots in r. In The R Journal (No. 2; Vol. 10, pp. 248–261). https://doi.org/10.32614/RJ-2018-051

Dixon, W. J. (1950). Analysis of extreme values. The Annals of Mathematical Statistics, 21(4), 488–506.

Dixon, W. J. (1951). Ratios involving extreme values. The Annals of Mathematical Statistics, 22(1), 68–78.

Fox, J., & Weisberg, S. (2019). An R companion to applied regression (Third). Sage. https://socialsciences.mcmaster.ca/jfox/Books/Companion/

Grubbs, F. E. (1969). Procedures for detecting outlying observations in samples. Technometrics, 11(1), 1–21.

Hofmann, H. (1994). Statlog (German Credit Data). UCI Machine Learning Repository.

Komsta, L. (2022). Outliers: Tests for outliers. https://CRAN.R-project.org/package=outliers

Millard, S. P. (2013). EnvStats: An r package for environmental statistics. Springer. https://www.springer.com

Rorabacher, D. B. (1991). Statistical treatment for rejection of deviant values: Critical values of dixon’s" q" parameter and related subrange ratios at the 95% confidence level. Analytical Chemistry, 63(2), 139–146.

Rosner, B. (1975). On the detection of many outliers. Technometrics, 17(2), 221–227.

Tietjen, G. L., & Moore, R. H. (1972). Some grubbs-type statistics for the detection of several outliers. Technometrics, 14(3), 583–597.

Wickham, H. (2016). ggplot2: Elegant graphics for data analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org

Wickham, H., François, R., Henry, L., & Müller, K. (2021). Dplyr: A grammar of data manipulation. https://CRAN.R-project.org/package=dplyr

Recuerda, que como lo hemos discutido en los capítulos anteriores, no toda anomalía es un outlier pero todo outlier es una anomalía.↩︎
El ETL típicamente es responsabilidad del ingeniero de datos, pero en algunas ocasiones a los científicos de datos les corresponde realizar esta tarea.↩︎
Como ocurre con cualquier prueba estadística, para rechazar o no la hipótesis nula podemos comparar el estadístico de prueba con el valor de la respectiva distribución o podemos emplear el valor p. Si el valor p es menor al nivel de significancia (generalmente \(\alpha=0.05\) o \(\alpha=0.01\)) entonces podemos afirmar que se rechaza la hipótesis nula con una confianza del \(100 \cdot (1 - \alpha)\)%. Por el contrario, si el valor p es mayor o igual al nivel de significancia, no se cuenta con evidencia suficiente para rechazar la hipótesis nula.↩︎
La traducción sería “empantanamiento” o “embarrada”. Un swamp es un pantano.↩︎
Esta prueba no la estudiamos en este capítulo.↩︎