8 Métricas de origen en el ML: distancia kNN y LOF

En los Capítulos 2, 3 y 6 estudiamos métodos de origen en la estadística para detectar anomalías puntuales y univariadas. En el Capítulo 4 discutimos cómo encontrar outliers multivariados puntuales. Como lo discutimos en el Capítulo 7, todas las métricas y pruebas empleadas hasta aquí tienen en común su origen en la estadística.

En este capítulo estudiaremos dos métricas cuyo origen se encuentra en el aprendizaje de máquina: la distancia kNN y el LOF (por la sigla del inglés Local Outlier Factor). Ambas son técnicas para detectar anomalías multivariadas puntuales o globales que tienen origen en métodos de aprendizaje de máquina. La diferencia entre estas aproximaciones es la filosofía de cómo encontrar las anomalías.

La distancia kNN, como su nombre lo indica, es un método basado en la distancia como aquellos estudiados en los Capítulos 2, 3 y 4. Intuitivamente, la distancia kNN busca encontrar observaciones que estén “lejos” de sus vecinos más próximos. Por otro lado, el LOF es un método basado en la densidad. Intuitivamente, el LOF busca encontrar observaciones que se encuentren en regiones de baja densidad de datos. En otras palabras, el LOF busca encontrar observaciones que estén alejadas de sus vecinos, pero cuyos vecinos estén “densamente” agrupados. En las secciones de este capítulo discutiremos cada una de estas métricas en detalle y cómo implementarlas en R.

8.1 Distancia kNN

Si te son familiares los modelos de clasificación, debes conocer el modelo de \(k\) vecinos más próximos (kNN por sus siglas en inglés k-nearest neighbors)59. Intuitivamente, el modelo kNN clasifica una observación basándose en la clase mayoritaria de sus \(k\) vecinos más cercanos. Por ejemplo, si \(k=5\)60 y 3 de los vecinos más cercanos a una observación pertenecen a la clase A y 2 a la clase B, entonces la observación se clasifica como A. La distancia kNN que emplearemos en este capítulo es un concepto que se deriva de dicho modelo.

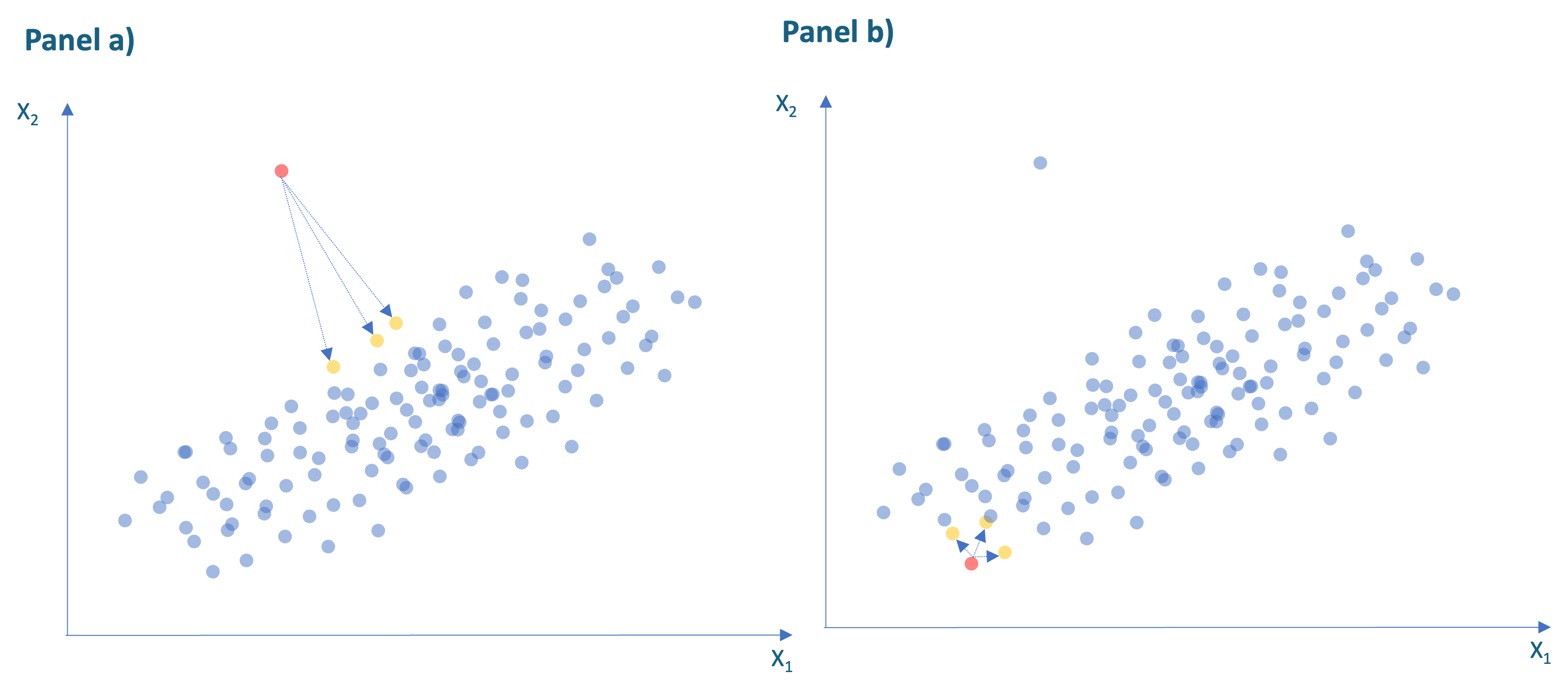
La distancia kNN mide la distancia promedio de un individuo a cada uno de los k individuos más cercanos. En la Figura 8.1 se ilustran las distancias para los tres vecinos más cercanos (\(k=3\)) de la observación en rojo. Las distancias individuales están representadas por las flechas azules y los tres vecinos más cercanos que se presentan en amarillo. En el panel a) se observa un punto con distancia promedio a los vecinos (kNN) relativamente grande y por tanto se considerará como una anomalía. Por otro lado, en el panel b) se presenta una observación con una distancia kNN (promedio)) relativamente pequeña. De esta manera, la distancia kNN proporciona una medida intuitiva de qué tan aislada está un individuo de sus vecinos, de tal manera que los valores más grandes son más probables de estar asociados a anomalías.



Figura 8.1: Relación entre las tareas de analítica y los tipos de analítica

Relación entre las tareas de analítica y los tipos de analítica
Fuente: elaboración propia.



Ramaswamy et al. (2000) propuso emplear la distancia kNN para detectar las observaciones que se encuentran “más alejadas” de las otras. En general, los pasos para encontrar la distancia kNN son:

  1. Estandarizar61 los datos.
  2. Seleccionar una observación y calcular la distancia de esta a cada una de las demás observaciones.
  3. Identificar los \(k\) vecinos más cercanos a la observación seleccionada.
  4. Calcular la distancia promedio del punto a sus \(k\) vecinos más cercanos.
  5. Repetir pasos 2 a 4 hasta agotar la muestra.

La distancia entre cada observación se puede calcular de diferentes maneras; por ejemplo, empleando la distancia euclidiana. Pero existen más tipos de distancias, como lo discutimos en la Sección 4.2.

La distancia euclidiana entre dos individuos se define como la distancia al cuadrado entre los dos vectores62. En otras palabras, se calcula la distancia cuadrada entre los dos individuos para cada una de las \(d\) dimensiones (variables), posteriormente se suman esas distancias y finalmente se regresan a la escala original calculando la raíz cuadrada63.

Formalmente, definamos el vector de las observaciones64 para las \(d\) variables para un individuo \(i\), como \(\mathbf{x_i}= [ x_{i,1} \quad x_{2,1} \quad \cdots \quad x_{i,d}]\). Entonces, la distancia euclidiana se define como:

\[\begin{equation} d(\mathbf{x_i},\mathbf{x_j}) = \sqrt{\left (\sum_{m = 1}^ {d} \left ( x_{i,m} - x_{j,m} \right)^{2} \right)}=\sqrt{ \left ( \mathbf{x_{i}} - \mathbf{x_{j}} \right)^{T} \left ( \mathbf{x_{i}} - \mathbf{x_{j}} \right) } \tag{8.1} \end{equation}\]

La distancia euclidiana es la medida de distancia más común, pero tiene un problema; a medida que aumenta la cantidad de variables involucradas en el cálculo de las distancias (dimensionalidad de los datos), la distancia euclidiana resulta menos útil65. Existen otras medidas como la de Chebyshev (o Distancia máxima), Manhattan, Canberra, Minkowski y binaria66.

La distancia de Chebyshev Distancia máxima o también conocida como la norma vectorial máxima se define como: \[\begin{equation} d(\mathbf{x_i},\mathbf{x_j}) = \max_{1 \leq m \leq d} \left | x_{i,m} - x_{j,m} \right | \tag{8.2} \end{equation}\]

La distancia de Manhattan también conocida como la distancia del taxi (en inglés Taxicab distance) o distancia de la manzana (en inglés City Block distance) está definida como: \[\begin{equation} d(\mathbf{x_i},\mathbf{x_j}) = \sum_{m = 1}^ {d} \left | x_{i,m} - x_{j,m} \right | \tag{8.3} \end{equation}\]

La distancia de Canberra es una versión ponderada de la distancia Manhattan que se define como:

\[\begin{equation} d(\mathbf{x_i},\mathbf{x_j}) = \sum_{m = 1}^ {d}{ \frac{\left | x_{i,m} - x_{j,m} \right |}{\left | x_{i,m} \right | + \left | x_{j,m} \right |}} \tag{8.4} \end{equation}\]

La distancia de Minkowski es una generalización de las tres primeras distancias anteriores. Esta se define como la norma vectorial de orden \(p\). Es decir, la distancia de Minkowski es la \(p\)-ésima raíz de la suma de las \(p\)-ésima potencia de las diferencias de los componentes. En otras palabras,

\[\begin{equation} d(\mathbf{x_i},\mathbf{x_j}) = \left (\sum_{m = 1}^ {d} \left ( x_{i,m} - x_{j,m} \right)^ {p} \right)^{\frac{1}{p}} \tag{8.5} \end{equation}\]

Nota que cuando \(p = 1\), entonces esta distancia es exactamente igual a la de Manhattan. Con \(p = 2\) esta distancia es igual a la euclidiana. Y finalmente, cuando \(p = \infty\) entonces obtendremos la distancia de Chebyshev.

Así, el primer paso para calcular la distancia kNN es estandarizar los datos. El segundo paso implica seleccionar una observación y calcularle a esa observación la distancia a todas las otras observaciones empleando alguna de las distancias discutidas anteriormente. Después, el tercer paso implica encontrar para esa observación seleccionada cuáles son las \(k\) observaciones que tienen la distancia más pequeña a ella; es decir, los \(k\) vecinos más cercanos. El cuarto paso es calcular la distancia promedio a la observación seleccionada de los \(k\) vecinos cercanos. Y finalmente, este procedimiento se repite para todas las observaciones de la muestra.

De esta manera, la distancia kNN se emplea para encontrar aquellas observaciones que tengan la distancia kNN más grande (la distancia promedio a sus \(k\) vecinos cercanos) de tal manera que se puede considerar como anomalía. Si el punto de datos se encuentra dentro del rango esperado de los \(k\) vecinos más cercanos, se considera un punto “normal” (no anómalo). Lastimosamente, no existe un umbral para determinar cuándo una distancia kNN se considera “grande”. La evaluación de si una distancia es grande o no dependerá del contexto.

Por otro lado, nota que para emplear este algoritmo, es necesario definir \(k\) (el número de vecinos cercanos). Está documentado que la elección del valor de \(k\) puede afectar sustancialmente los resultados de la detección de anomalías. Un valor de \(k\) demasiado pequeño puede conducir a la detección de falsos positivos, mientras que un valor demasiado grande puede omitir anomalías reales. En la práctica, se recomienda probar diferentes valores de \(k\) y evaluar la estabilidad de los resultados.

8.2 LOF

El LOF (Local Outlier Factor, que sería algo así como factor de “atípicidad” local) es una técnica para detectar anomalías propuesta por Breunig et al. (2000) que, a diferencia de métodos basados en la distancia como la distancia kNN, busca encontrar la densidad local para cada observación. Y empleando dicha densidad identifica como anomalías aquellos puntos que se encuentran en regiones de baja densidad.

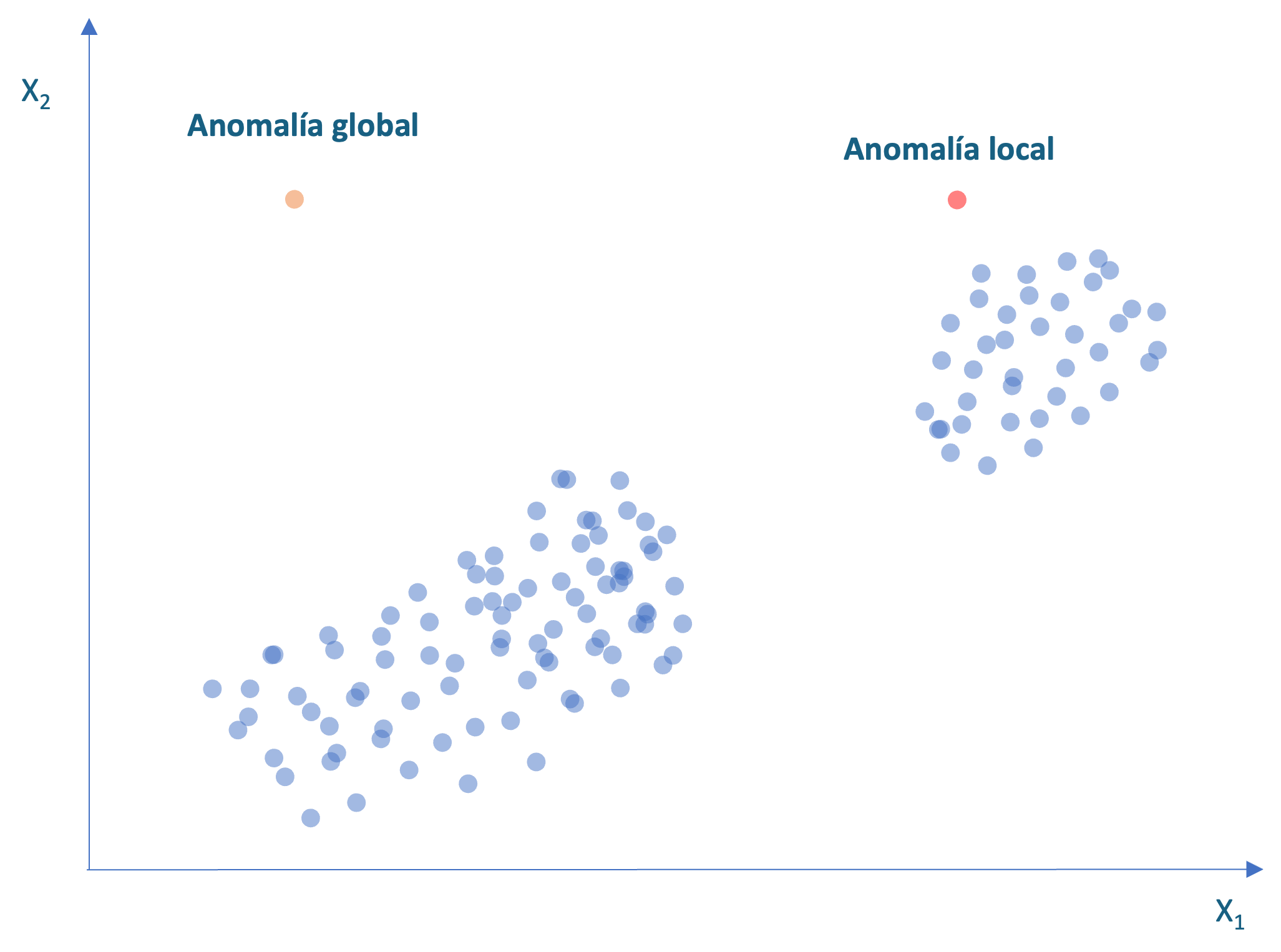
La distancia kNN es una métrica buena para detectar puntos que están realmente lejos de sus vecinos (anomalías globales). Por ejemplo, en la Figura 8.2 el punto naranja (situado en la parte superior izquierda) tendrá la distancia kNN más grande y por tanto será marcado como una anomalía. No obstante, un punto como el rojo (parte superior derecha) no es detectado como una anomalía por la distancia kNN porque está relativamente cerca de sus vecinos más cercanos y, por tanto, tiene una distancia kNN baja. Sin embargo, esa observación se encuentra alejada de sus vecinos más próximos, que están “densamente” agrupados. Este tipo de observaciones se denominan anomalías locales y se identifican más fácilmente con el LOF.



Figura 8.2: Anomalía global y local

Anomalía global y local
Fuente: elaboración propia.



El LOF para una observación se define como la densidad promedio alrededor de los \(k\) vecinos más próximos del individuo dividida por la densidad alrededor del propio individuo.

Antes de estudiar la formalidad del LOF, veamos un poco la intuición detrás de este factor. Consideremos una observación como el punto A en rojo en el panel a) de la Figura 8.3 y supongamos que \(k\) = 3.

El primer paso es considerar los 3 vecinos más cercanos a esta observación (Ver observaciones en naranja en el panel b) de la Figura 8.3). Para determinar la densidad del punto A, calculamos la distancia de cada vecino a la observación analizada. Y en vez de sacar el promedio de las distancias de los vecinos, como se hace en el método de la distancia kNN, consideramos la distancia más grande y esta se convierte en el radio del área para establecer la densidad del punto A. Noten que entre más grande es el radio, más baja es la densidad de puntos al rededor del punto bajo observación.



Figura 8.3: Ejemplo del cálculo del LOF

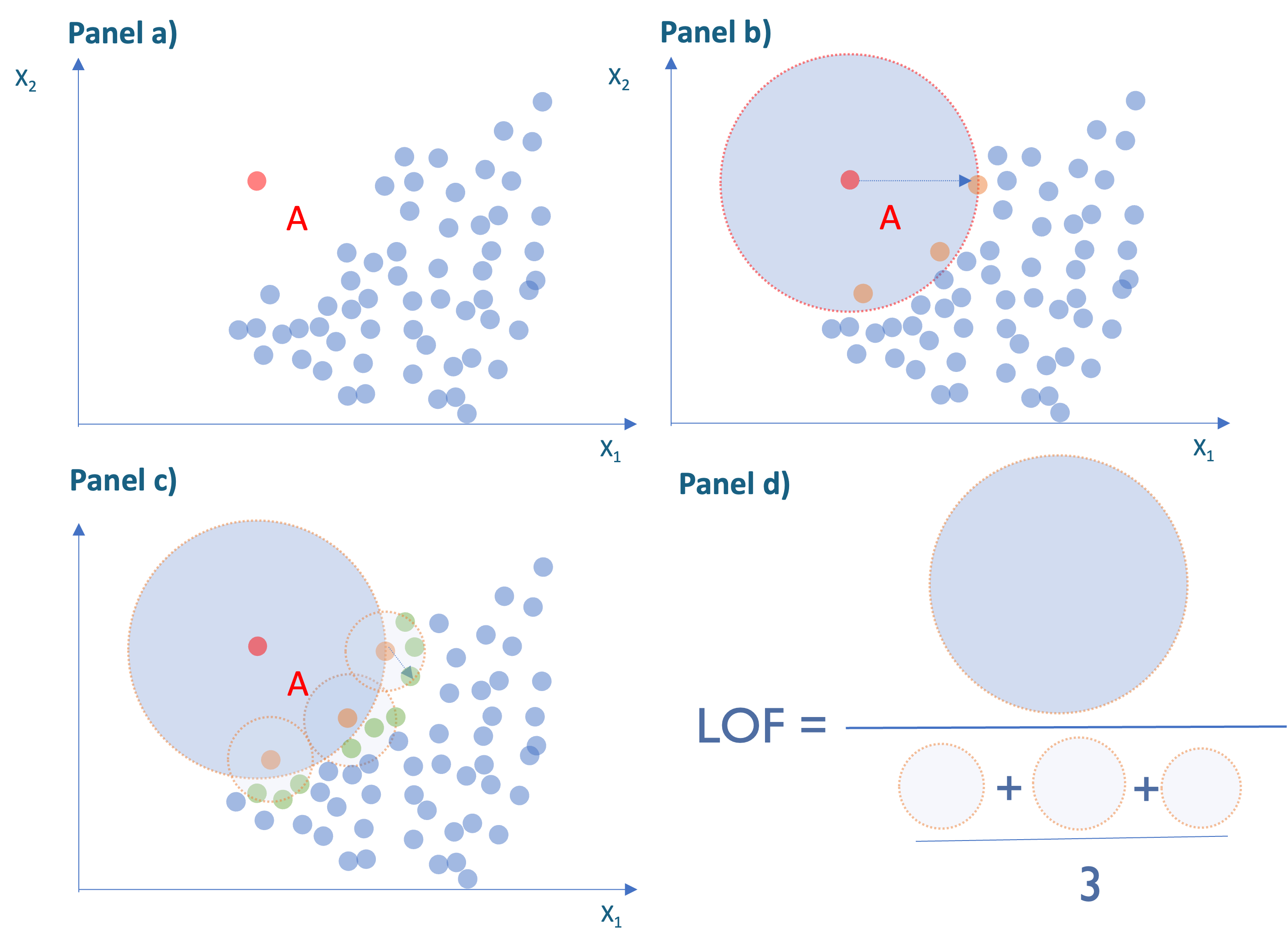
Ejemplo del cálculo del LOF
Fuente: elaboración propia.



Ahora realizamos el mismo ejercicio de establecer la densidad para cada uno de los vecinos de A (Ver panel c) de la Figura 8.3). Finalmente, el LOF para el individuo A es la razón entre el área de la densidad de A y el promedio de sus vecinos. Nota que en este caso el LOF será mayor que uno, lo cual es un indicador de que probablemente es una anomalía; más adelante discutiremos esto en detalle.

Recordemos que hemos definido \(d(x_i,x_j)\) como la distancia entre las observaciones \(i\)-ésima y \(j\)ésima. Además, sean:

  • \(d_{i,k}\): la distancia entre la observación \(i\)-ésima y \(k\)-ésimo vecino más próximo.
  • \(N_{i,k}\): el conjunto de \(k\) vecinos más próximos dentro de \(d_{i,k}\) de67 \(x_i\).
  • \(r_k(x_i,x_j) = \max(d_{i,k},d(x_i,x_j))\): es el “alcance” (en inglés reachability) de \(x_i\) desde \(x_j\). Es decir, \(r_k(x_i,x_j)\) es la distancia entre las observaciones \(x_i\) y \(x_j\) cuando están alejados entre sí, pero es igual a \(d_{i,k}\) si \(x_i\) es uno de los \(k\) vecinos más cercanos de68 \(x_j\).

Siguiendo a Breunig et al. (2000), podemos definir la densidad de “alcance” local (en inglés local reachability density) de la observación \(x_i\) (\(lrd_k(x_i)\)) como69:

\[\begin{equation} lrd_k(x_i)=\frac{1}{\frac{\sum_{x_j \in N_{i,k}}r_k(x_i,x_j)}{N_{i,k}}} \tag{8.6} \end{equation}\]

El LOF corresponde al cociente de la media de los \(lrd_k(x_i)\) de todos los \(k\) vecinos y el lrd de ese punto. Es decir, \[\begin{equation} LOF_k(x_i)=\frac{\sum_{x_j \in N_{i,k}}\frac{lrd_k(x_j)}{lrd_k(x_i)}}{N_{i,k}}=\frac{\sum_{x_j \in N_{i,k}}lrd_k(x_j)}{N_{i,k} \cdot lrd_k(x_i)} \tag{8.7} \end{equation}\]

Esto proporciona una medida relativa de la densidad de cada observación en comparación con sus vecinos. Se considera que una observación es anómala si se encuentra en una región de baja densidad (lejos de sus vecinos) mientras que sus vecinos se encuentran en regiones de mayor densidad (con muchos vecinos cerca). Un valor de \(LOF_k(x_i)\) mucho mayor que 1 puede ser señal de que la observación tiene un reachability promedio mucho mayor en comparación con sus vecinos, por lo que se considera una anomalía.

Una de las ventajas del LOF frente a la distancia kNN es precisamente la interpretación más sencilla. En este caso tenemos que:

  • Si \(LOF_k(x_i) > 1\) entonces es probable que la observación \(i\) sea una anomalía
  • Si \(LOF_k(x_i) \leqslant 1\) entonces es poco probable que la observación \(i\) sea una anomalía

Así, en la práctica, cuanto más lejos de uno sea el LOF para una observación, se considera una anomalía, ya que es significativamente más raro que sus vecinos, indicando que se encuentra en una región de baja densidad. Y entre más cerca esté el LOF de una observación a 0, se considerará la observación como normal, ya que su densidad local es similar a la de sus vecinos.

Dado que el LOF es un método basado en la densidad (local) y no en la distancia como la distancia kNN, es más robusto a los outliers que la distancia kNN. En ambos casos se requiere definir el número de vecinos (\(k\)).

8.3 Implementación en R

Para estudiar cómo implementar las aproximaciones estudiadas emplearemos los mismos datos que empleamos en los Capítulos 2, 3 y 4. Los datos provienen de Hofmann (1994) y se encuentran en el archivo datos_credito.RData que se puede descargar de la página web del libro (https://www.icesi.edu.co/editorial/deteccion-anomalias). La descripción de las variables se encuentra en la Sección 2.4. Carguemos los datos:

load("./datos/datos_credito.RData")

Los datos están cargados en el objeto de clase data.frame que denominamos german. Ese objeto tiene 14 variables y 1000 clientes. Seleccionemos solo las variables cuantitativas para poder aplicar las técnicas estudiadas en las secciones anteriores. Empleemos la función select_if() del paquete dplyr (Wickham et al., 2021) para hacer esta tarea más sencilla. Y finalmente estandaricemos los datos empleando la función scale() de la base de R. 

library(dplyr)
german_cuanti_est <- german %>% 
     select_if(is.numeric) %>% 
    scale()

8.3.1 Detectando anomalías con la distancia kNN

Para calcular la distancia kNN existen diferentes funciones, en este libro emplearemos la función kNNdist() del paquete dbscan (Hahsler et al., 2019). Esta función típicamente incluye los siguientes argumentos:

kNNdist(x, k, all)

donde:

  • x: Una matriz de datos, un objeto de clase dist (distancia) o un objeto de clase kNN.
  • k: Número de vecinos.
  • all: Un valor lógico para expresar si se quieren que se calcule la distancia kNN para todos los posibles vecinos hasta el establecido en k. Por defecto, all = FALSE.

Si como argumento se le entrega a esta función un objeto con datos, entonces la distancia kNN será calculada empleando la distancia euclidiana. Si deseamos calcular la distancia kNN con otro tipo de distancia, podemos emplear un objeto de clase dist que previamente haya calculado la distancia con el método deseado. Esta función, a diferencia de la mayoría de las funciones disponibles en otros paquetes, es de las pocas que permite la inclusión de otro tipo de distancias diferentes a la euclidiana.

Para nuestro caso, el código para calcular la distancia kNN para 10 vecinos, empleando la distancia euclidiana, es:

# Cargar paquete
library(dbscan)

# Calcular la distancia kNN con distancia euclidiana.

anomalias_DkNN <- kNNdist(german_cuanti_est, k =10)

En el objeto anomalias_DkNN obtenemos las distancias kNN para todas las observaciones. Con la siguiente línea de código podemos ver la observación con la mayor distancia kNN: 

# Identificar el número de la observación con la distancia kNN más grande

which.max(anomalias_DkNN)
## [1] 757
# La distancia kNN mas alta

anomalias_DkNN[which.max(anomalias_DkNN)]
## [1] 3.81735

También podemos visualizar las distancias kNN con un boxplot (ajustado según Hubert & Vandervieren (2008)) como el que se presenta en la Figura 8.470.



Figura 8.4: Boxplot ajustado según Hubert y Vandervieren (2008) para la distancia kNN (k=10 y distancia euclidiana)

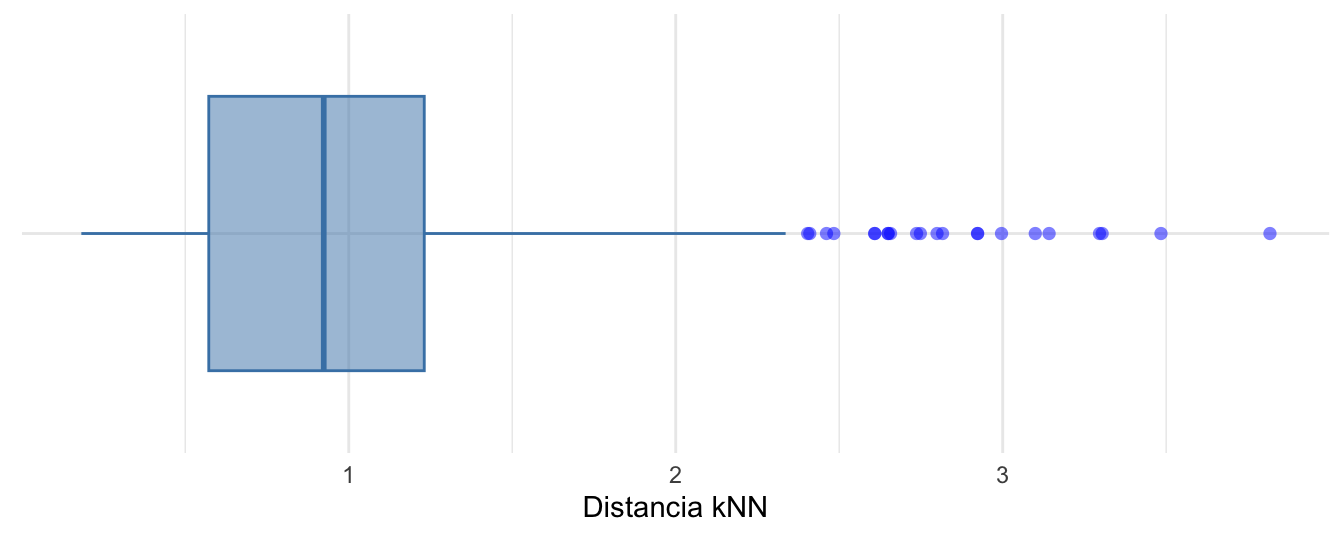
Boxplot ajustado según Hubert y Vandervieren (2008) para la distancia kNN (k=10 y distancia euclidiana)
Fuente: elaboración propia.



En la Figura 8.4 podemos ver que existen 22 valores anómalos. Es decir, observaciones con distancias kNN relativamente grandes.

Otra alternativa para visualizar las distancias kNN es la función kNNdistplot() del paquete dbscan; ¡intenta usar esta función!

Nota que el \(k\) de 10 fue seleccionado arbitrariamente. En la práctica deberíamos emplear diferentes valores de \(k\) y ver qué tan robusta es nuestra decisión. Por ejemplo, calculemos la distancia kNN hasta 100 vecinos.

# Calcular la distancia kNN con distancia euclidiana hasta 100 vecinos.

anomalias_DkNN_100 <- kNNdist(german_cuanti_est, k =100, all = TRUE)

# identificar la observación con el mayor kNN para cada uno de los números de vecinos (columnas)
apply(anomalias_DkNN_100,2,which.max)
##   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20 
## 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 
##  21  22  23  24  25  26  27  28  29  30  31  32  33  34  35  36  37  38  39  40 
## 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 
##  41  42  43  44  45  46  47  48  49  50  51  52  53  54  55  56  57  58  59  60 
## 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 
##  61  62  63  64  65  66  67  68  69  70  71  72  73  74  75  76  77  78  79  80 
## 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 
##  81  82  83  84  85  86  87  88  89  90  91  92  93  94  95  96  97  98  99 100 
## 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757 757

Podemos observar que sin importar el número de vecinos que empleemos, la observación 757 es considerada una anomalía.

Por otro lado, si queremos emplear otra distancia podemos emplear la función dist() que está en el paquete central de R. El argumento method determina el tipo de medida de distancia que se quiere emplear. Las opciones para este argumento son: “euclidean”, “maximum”, “manhattan”, “canberra”, “binary” o “minkowski”. Por defecto, method = “euclidean”. Así mismo, está el argumento p para establecer la potencia que se desea emplear para la distancia de Minkowski, , por defecto p = 2.

Por ejemplo, para calcular la distancia kNN (para \(k=10\)) empleando la distancia de Chebyshev (o Distancia máxima) podemos emplear las siguientes líneas de código:

# Calcular Matriz de distancia de Chebyshev 
dist_Chebyshev <- dist(german_cuanti_est, method = "maximum")


# Calcular la distancia kNN con distancia de Chebyshev .

anomalias_DkNN_Chebyshev  <- kNNdist(dist_Chebyshev, k =10)


# Identificar el número de la observación con la distancia kNN más grande

which.max(anomalias_DkNN_Chebyshev)
## [1] 891
# La distancia kNN mas alta

anomalias_DkNN_Chebyshev[which.max(anomalias_DkNN_Chebyshev)]
## [1] 2.761777

Y visualicemos estas nuevas distancias kNN con un boxplot (ajustado según Hubert & Vandervieren (2008))) como el que se presenta en la Figura 8.571.



Figura 8.5: Boxplot ajustado según Hubert y Vandervieren (2008) para la distancia kNN (k=10 y distancia de Chebyshev)

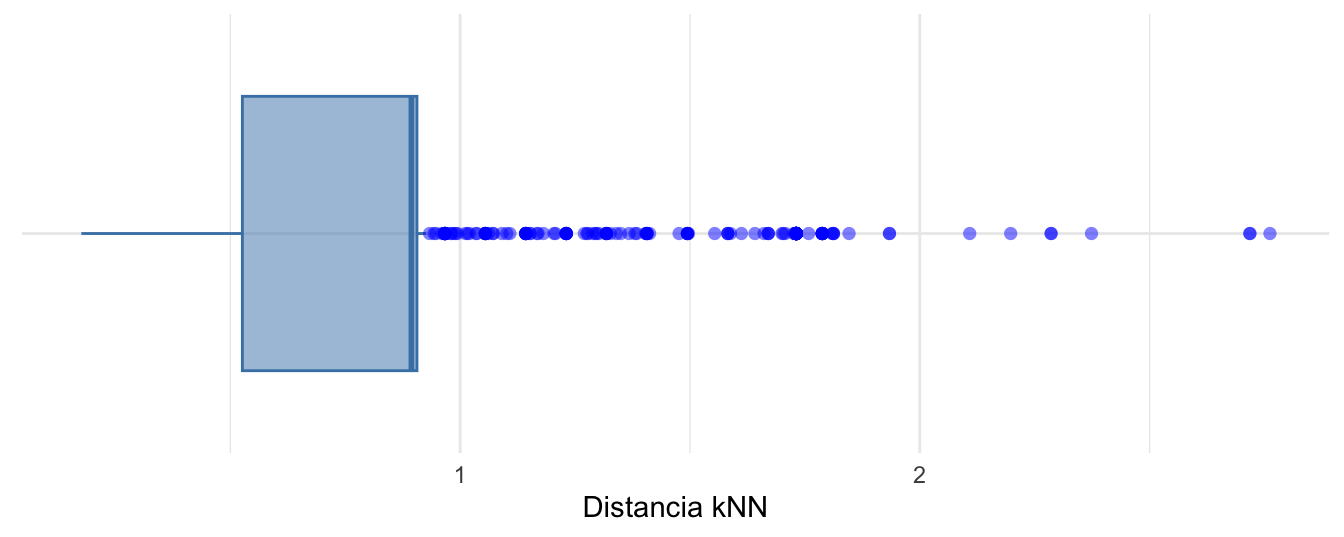
Boxplot ajustado según Hubert y Vandervieren (2008) para la distancia kNN (k=10 y distancia de Chebyshev)
Fuente: elaboración propia.

En la Figura 8.5 podemos ver que existen 185 valores anómalos. Es decir, observaciones con distancias kNN relativamente grandes.

8.3.2 Detectando anomalías con LOF

Para calcular LOF existen diferentes funciones. No obstante, en este libro, seguiremos empleando las funciones provistas por el paquete dbscan (Hahsler et al., 2019). En este caso, la función que nos permite calcular el LOF es lof(). Esta función típicamente incluye los siguientes argumentos:

lof(x, minPts = 5)

donde:

  • x: Una matriz de datos, un objeto de clase dist (distancia) o un objeto de clase kNN.
  • minPts: Número de vecinos. Al igual que la función kNNdist(), si a esta función se le entrega como argumento x un objeto con datos, entonces el LOF será calculado empleando la distancia euclidiana. Si deseamos calcular el LOF con otro tipo de distancia, podemos emplear un objeto de clase dist que previamente haya calculado la distancia con el método deseado, como se mostró anteriormente.

En este caso para calcular el LOF para nuestros datos con 10 vecinos, tendremos:

# Cargar paquete
library(dbscan)

# Calcular LOF con distancia euclidiana.

anomalias_LOF<- lof(german_cuanti_est, minPts = 10)

Filtremos las observaciones que tengan un LOF mayor a uno.

anomalias_LOF_org <- as.data.frame(anomalias_LOF) %>% 
  mutate(id = row_number()) %>% 
  filter(anomalias_LOF >1) %>% 
  arrange(desc(anomalias_LOF))

Nota que en este caso se encuentran 763 observaciones con un LOF por encima de 1. La observación con el LOF más grande es la 139 con un LOF de 4.1198627. Esta observación parece ser una anomalía local. Ahora, puedes chequear tu mismo la consistencia de este resultado para diferentes valores de \(k\). ¡Inténtalo!

8.4 Comentarios finales

En este capítulo hemos explorado las técnicas de distancia kNN y LOF para la detección de anomalías multivariadas. Hemos discutido cómo calcular la distancia kNN empleando diferentes distancias, como la distancia euclidiana y la de Chebyshev, y cómo representar visualmente las distancias resultantes usando boxplots ajustados. La distancia kNN permite detectar anomalías globales, así como las técnicas que estudiamos en los Capítulos 2, 3, 4 y 6.

Además, hemos estudiado el proceso de cálculo de LOF y la identificación de observaciones anómalas basándonos en un umbral de uno. Esta aproximación permite identificar anomalías locales (también conocidas como contextuales), esta es una gran diferencia con todos los métodos que hemos estudiado hasta el momento en este libro. En los próximos capítulos continuaremos estudiando herramientas que permiten detectar anomalías locales.

El LOF es una herramienta poderosa para la detección de anomalías individuales debido a su enfoque en la densidad local, pero esta ventaja es una desventaja para identificar anomalías grupales. Para detectar anomalías grupales, se pueden emplear técnicas que analicen las relaciones y patrones en subconjuntos más grandes de datos, como lo veremos en los Capítulo 9 y 10.

Ya hemos adquirido una base sólida en la detección univariada y multivariada de anomalías a través de técnicas tanto estadísticas como de aprendizaje de máquina. Sin embargo, vale la pena mencionar que nuestro viaje en este campo está lejos de terminar. En los siguientes capítulos, profundizaremos en estos métodos para ampliar aún más nuestra caja de herramientas para la detección de anomalías.



Referencias

Alonso, J. C., & Hoyos, C. C. (2025). Una introducción a los modelos de clasificación empleando r. Universidad Icesi. https://doi.org/https://doi.org/10.18046/EUI/bda.h.5
Alonso, J. C., Hoyos, C. C., & Largo, M. F. (2025). Una introducción a los modelos de clústering empleando r. Universidad Icesi. https://doi.org/https://doi.org/10.18046/EUI/bda.h.6
Breunig, M. M., Kriegel, H.-P., Ng, R. T., & Sander, J. (2000). LOF: Identifying density-based local outliers. Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, 93–104. https://doi.org/10.1145/342009.335388
Hahsler, M., Piekenbrock, M., & Doran, D. (2019). dbscan: Fast density-based clustering with R. Journal of Statistical Software, 91(1), 1–30. https://doi.org/10.18637/jss.v091.i01
Hofmann, H. (1994). Statlog (German Credit Data). UCI Machine Learning Repository.
Hubert, M., & Vandervieren, E. (2008). An adjusted boxplot for skewed distributions. Computational Statistics & Data Analysis, 52(12), 5186–5201.
Ramaswamy, S., Rastogi, R., & Shim, K. (2000). Efficient algorithms for mining outliers from large data sets. Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, 427–438.
Wickham, H., François, R., Henry, L., & Müller, K. (2021). Dplyr: A grammar of data manipulation. https://CRAN.R-project.org/package=dplyr

  1. Puedes ver Alonso & Hoyos (2025) para una introducción a los modelos de clasificación.↩︎

  2. Es decir, se consideran 5 vecinos para clasificar cada observación.↩︎

  3. Es decir, se emplean variables centradas (se resta la respectiva media) y con varianza igual (se divide cada una por la respectiva desviación estándar) para evitar que las escalas de medición de las variables y su volatilidad afecten el resultado, a esto lo llamaremos estandarizar los datos.↩︎

  4. Esta es la norma vectorial de orden 2.↩︎

  5. Esta es la razón por la que los datos originales deben ser centrados, como se discutirá más adelante. Es decir, se emplean variables centradas (se resta la media) y escaladas (divididas por su desviación estándar) para evitar que las escalas de medición de las variables afecten el resultado, a esto lo llamaremos estandarizar los datos.↩︎

  6. Como se mencionó anteriormente, típicamente estas variables estarían centradas en un ejercicio de detección de anomalías.↩︎

  7. Esto se conoce como la “maldición de la dimensionalidad”. ↩︎

  8. Ver Sección 2.2 de Alonso et al. (2025) para una discusión de esas medidas de distancia.↩︎

  9. Si hay múltiples observaciones todas exactamente a \(d_{i,k}\) de \(x_i\), entonces \(N_{i,k}\) puede contener más de \(k\) observaciones, pero por simplicidad omitiremos este caso. Es decir, puedes suponer que \(N_{i,k} = k\). Por otro lado, nota que una observación \(x_j\) puede estar dentro de \(N_{i,k}\), mientras que \(x_i\) no está en el conjunto \(N_{j,k}\) como se puede observar en los puntos verdes del panel c de la Figura 8.3.↩︎

  10. Nota que reachability es parecida a la distancia euclidiana pero truncada para que no sea menor a \(d_{j,k}\).↩︎

  11. Nota que el \(lrd_k(x_i)\) corresponde a la reachability promedio de la observación \(x_i\) hacia sus \(k\) vecinos más próximos. El denominador de esta expresión es equivalente al denominador representado en el panel d) de la Figura 8.3.↩︎

  12. Intencionalmente se omite el código que genera la Figura 8.4. ¡Intenta reproducir esta visualización!↩︎

  13. Intencionalmente se omite el código que genera la Figura 8.4. ¡Intenta reproducir esta visualización!↩︎