2 Estadísticas descriptivas para detectar anomalías univariadas

2.1 Introducción

Los problemas de detección de anomalías tienen múltiples facetas y las técnicas de detección de anomalías son muy diferentes. En el Capítulo 1 definimos anomalía como una observación o un conjunto de ellas que no parece seguir el mismo patrón que el resto de los datos en una o varias de sus características. También vimos cómo los tipos de valores anómalos pueden ser muy diferentes. Adicionalmente hemos hablado de diferentes aproximaciones para la detección de anomalías que nacen desde la estadística y desde el aprendizaje de máquina. En este capítulo nos concentraremos en técnicas estadísticas para la detección de anomalías que se emplean en los análisis estadísticos de datos.

Antes de continuar, recordemos que en el contexto de la estadística un outlier es una observación que se desvía significativamente del resto de la muestra, ya sea en una o varias de sus características (features o variables)¹⁷. Como lo discutimos en el Capítulo 1, todo outlier es una anomalía, pero no toda anomalía es un outlier. Recuerda que el concepto de anomalía es más amplio que el de outlier, pues abarca no solo desviaciones puntuales extremas respecto de una distribución, sino también irregularidades dependientes del contexto y patrones colectivos. En este capítulo nos concentraremos en detectar anomalías puntuales univariadas con métodos estadísticos descriptivos. Así, en sentido estricto, en este capítulo estudiaremos métodos para detectar outliers en una sola variable que se emplean en el análisis estadístico de datos.

Cuando se realiza un análisis estadístico de datos, es común que se inicie con un análisis exploratorio de los datos. El análisis exploratorio de los datos, también conocido por su sigla en inglés EDA (Exploratory Data Analysis), implica examinar y analizar la muestra para comprender su estructura, características y patrones. El EDA se realiza utilizando una combinación de técnicas visuales y estadísticas, con el objetivo de:

Obtener una visión general de los datos: Esto incluye comprender el tipo de datos, la distribución de las variables, su tendencia central y volatilidad, así como la presencia de valores atípicos (outliers) y las relaciones entre las variables.
Identificar patrones y tendencias: El EDA puede ayudar a descubrir patrones y tendencias interesantes en los datos que podrían no ser evidentes a simple vista.
Formular hipótesis: El EDA puede ayudar a formular hipótesis sobre las relaciones entre las variables y los posibles factores que influyen en los resultados.
Guiar el proceso de limpieza de los datos: El EDA puede ayudar a identificar y corregir problemas en los datos, como valores faltantes o inconsistencias, antes de realizar análisis estadísticos más formales.

De hecho, el primer objetivo está relacionado directamente con la tarea de detectar outliers¹⁸. Recuerda que en el análisis tradicional estadístico es importante detectar los valores atípicos, pues estos pueden generar que algunas técnicas estadísticas o estimadores no funcionen bien o no provean una buena idea de lo que está ocurriendo con la muestra. Por esto, el primer paso de cualquier análisis de anomalías típicamente inicia con un EDA. Al analizar los datos es importante distinguir entre los outliers univariados y multivariados.

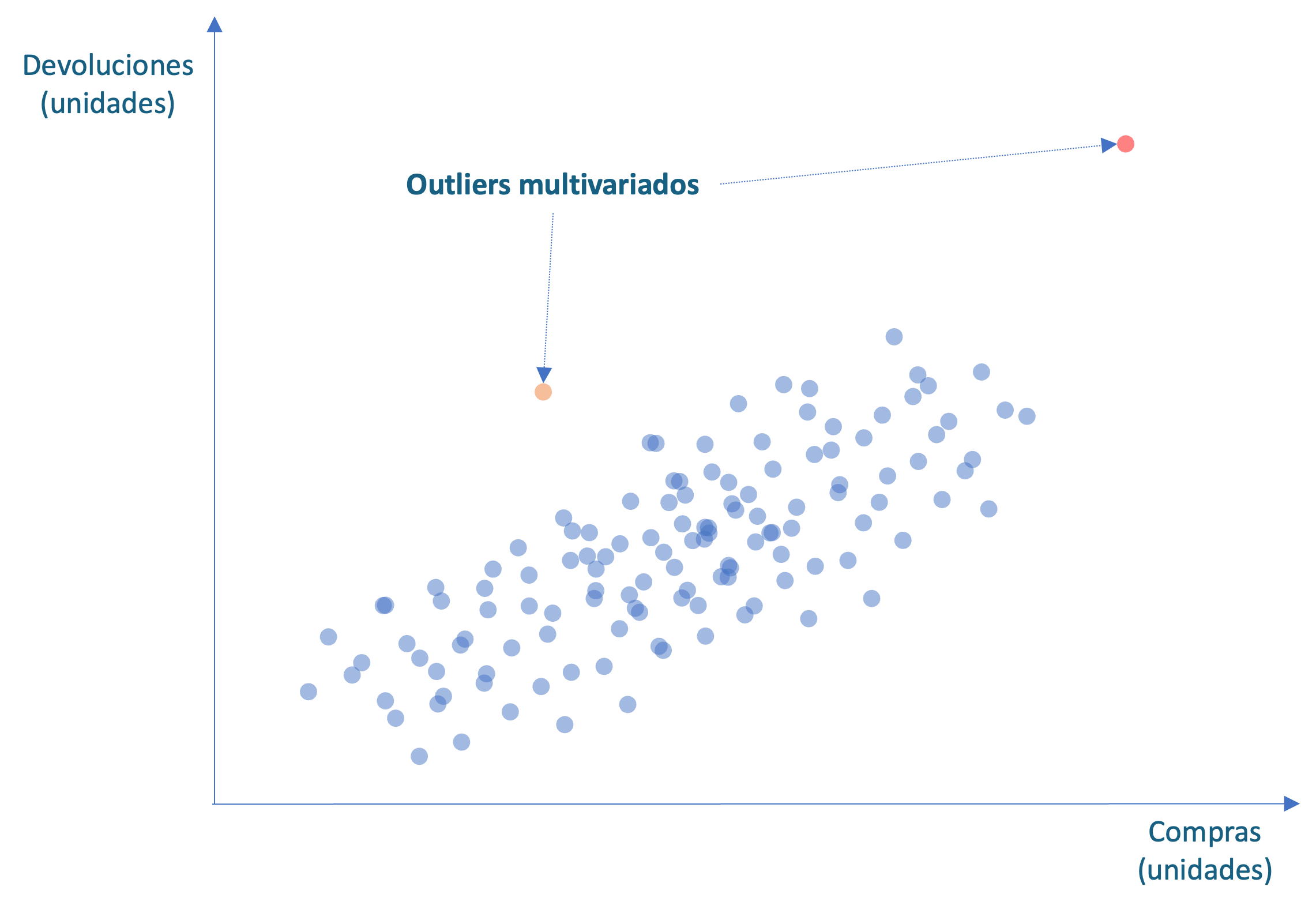
Recuerda que en el Capítulo 1 definimos un outlier univariado como una observación que se desvía significativamente del resto en una sola variable. Estos datos pueden ser el resultado de errores de medición, errores de registro o eventos inusuales. Por otro lado, también definimos un outlier multivariado como una observación que se desvía significativamente del resto en múltiples variables simultáneamente. A diferencia de los outliers univariados que se destacan en una sola variable, los outliers multivariados rompen el patrón por completo. Esta observación anómala puede ser el resultado de una combinación de factores, como errores de medición, errores de registro o eventos inusuales que ocurren en varias variables al mismo tiempo. La detección de outliers multivariados es más compleja que la detección de outliers univariados, ya que requiere considerar las relaciones entre las variables. Por ejemplo, en la Figura 2.1 podemos identificar una observación atípica multivariada (en rojo) que se distancia del patrón de las otras observaciones, pero si consideramos cada una de esas variables de manera individual, no se observa un dato atípico. Ahí es cuando se presenta la dificultad para identificar esta anomalía.

Figura 2.1: Ejemplo de anomalías multivariadas

Fuente: elaboración propia.

Por ejemplo, si observamos para una de las 1000 tiendas de una organización unas ventas muy superiores a las demás en el año anterior, entonces estamos frente a un outlier univariado. Esto podría ser fruto de un error de registro, una estrategia de marketing excepcional o un fraude.

Por otro lado, consideramos un caso en el que tenemos dos features (variables) para cada cliente: unidades compradas y unidades devueltas (Ver Figura 2.1). De los miles de clientes de una organización, podríamos tener un cliente con compras inusualmente grandes y devoluciones de artículos relativamente grandes (Ver punto naranja en la Figura 2.1). Este cliente será un outlier multivariado¹⁹. También podemos encontrar un cliente que tiene compras muy parecidas al promedio y devoluciones ligeramente superiores al promedio (Ver punto rojo en la Figura 2.1). Este cliente se distancia del patrón que siguen los otros clientes y, por tanto, sería un outlier multivariado, si bien el cliente no presenta valores inusualmente diferentes al resto de clientes para cada variable. Lo que hace anómalo a este individuo es la combinación de valores para las dos variables. Esto podría indicar un fraude, un error en el registro o un problema con el producto o servicio recibido por ese cliente.

En este capítulo nos concentraremos en detectar anomalías univariadas; en el Capítulo 4 estudiaremos las técnicas estadísticas basadas en métricas para encontrar outliers multivariados.

Regresando al EDA, típicamente un EDA implica por lo menos los siguientes pasos:

Graficar los datos: Hacer gráficas de los datos es una herramienta importante para el inicio de un EDA pues nos permite entender gráficamente lo que ocurre con nuestra muestra. Típicamente se emplean gráficos como histogramas para ver la distribución de cada variable y, en especial, los boxplot²⁰ para hacer visibles los outliers. Así mismo, los diagramas de dispersión se suelen emplear para detectar los valores atípicos multivariados.
Calcular estadísticas descriptivas para cada variable (análisis univariado): En este paso, se analiza cada variable y dependiendo del tipo (numérica, categórica, etc.) se calculan estadísticas de tendencia central, dispersión, posición (por ejemplo como los cuartiles) y forma.

En este capítulo estudiaremos algunas de las métricas de origen estadístico más populares empleadas en un EDA para detectar valores atípicos y repasaremos las dos gráficas más comunes cuando se está indagando por valores atípicos: el histograma y el boxplot.

2.2 Aproximación gráfica

Los gráficos más empleados para detectar outliers univariados son los histogramas y los boxplots. Recuerden que un histograma agrupa los datos en intervalos pequeños que se miden típicamente en el eje horizontal, y en el eje vertical se representa la frecuencia de aparición de las observaciones dentro de los límites del intervalo.

No obstante, el histograma presenta la distribución de los datos, el boxplot fue diseñado por Tukey (1970) para detectar outliers²¹. El boxplot o diagrama de cajas²² permite observar el primer, segundo (mediana) y tercer cuartil, la distancia intercuartílica (distancia entre el primer y tercer cuartil de los datos) y la existencia o no de datos atípicos.

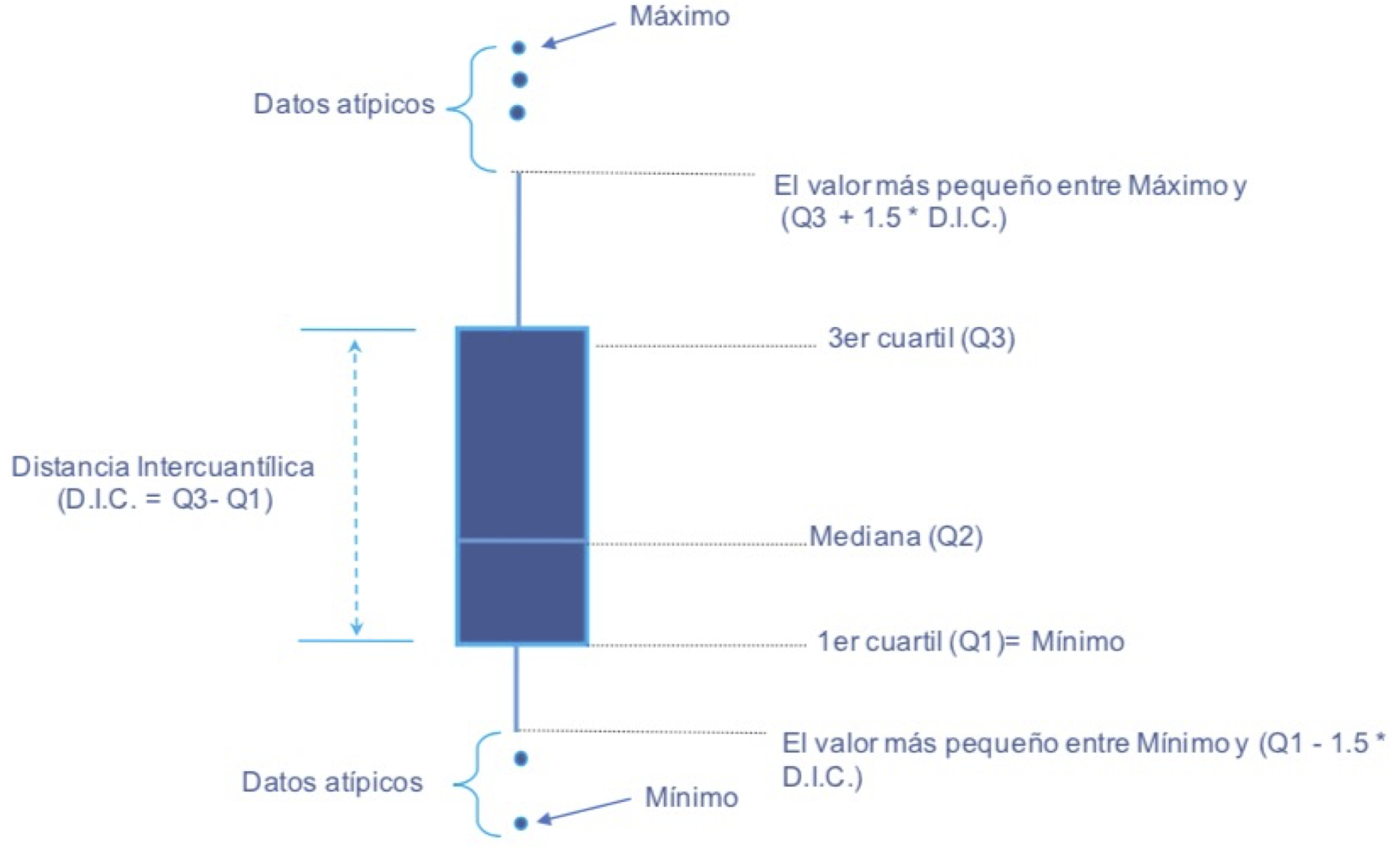
La caja central del boxplot se extiende desde el primer cuartil (Q1) hasta el tercer cuartil (Q3) (Ver Figura 2.2). De esta manera, el 50% de los datos están contenidos en la caja. Dentro de la caja, se traza una línea que marca la mediana (Q2) de los datos (Ver Figura 2.2). La longitud de la caja se conoce como Distancia intercuartílica (DIC) o rango intercuartílico (IQR). Por otro lado, tenemos los bigotes (Whiskers en inglés) que son las líneas que se extienden de los extremos de la caja. El bigote superior se extiende desde el extremo superior de la caja (Q3) a lo que sea menor entre el valor máximo de las observaciones o 1.5 veces el IQR (o DIC). Y el otro bigote sale de la parte inferior de la caja (Q2) hasta lo que sea más pequeño entre el valor mínimo de los datos y 1.5 veces el IQR (o DIC). Los bigotes indican la variabilidad de los datos fuera de los cuartiles superior e inferior. Si existen observaciones que se encuentren por fuera de los bigotes, estas observaciones se representan con un punto y se consideran valores atípicos (Ver Figura 2.2).

Figura 2.2: Elementos de un Boxplot

Fuente: tomado de Alonso y Largo (2024).

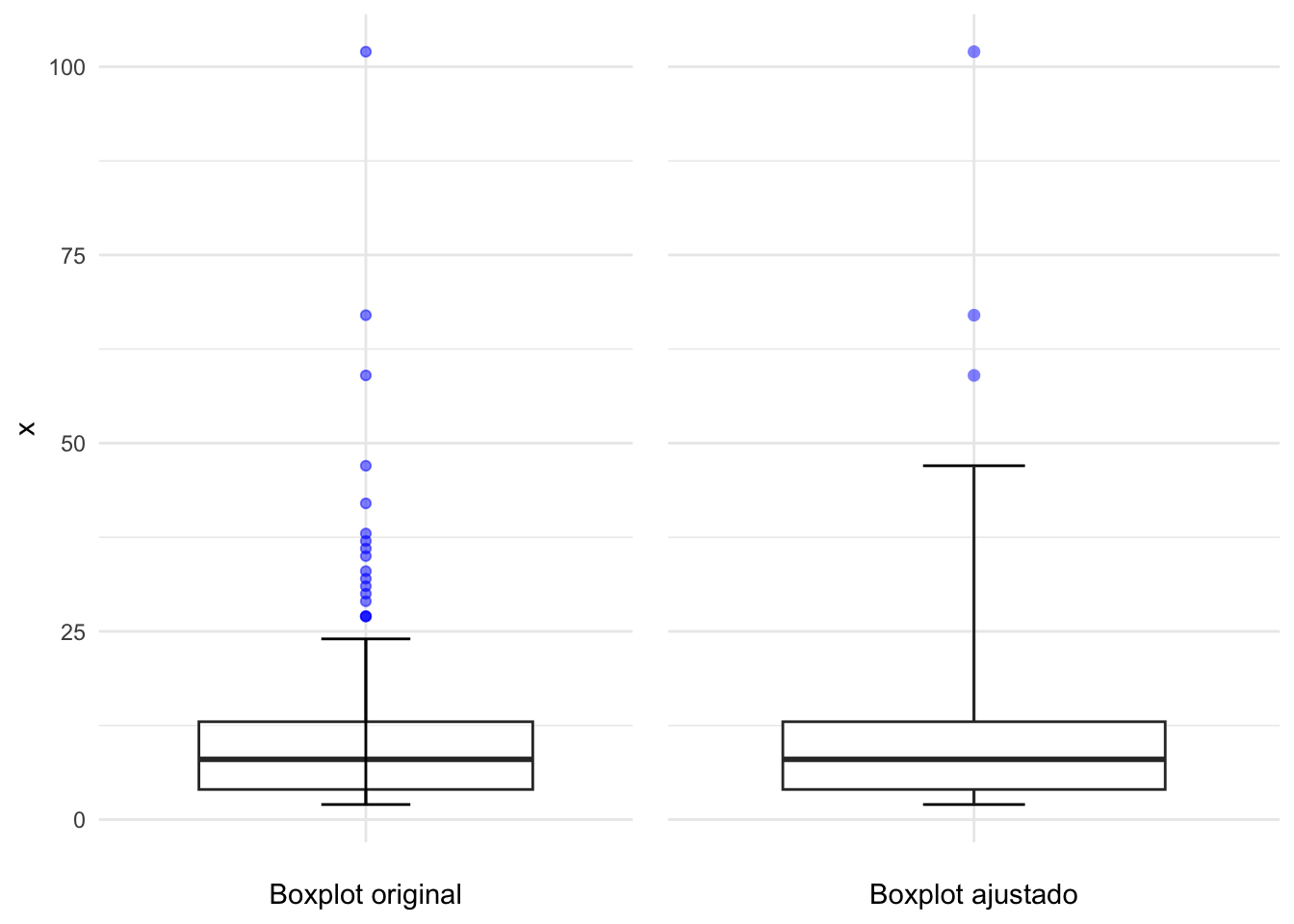
En distribuciones asimétricas, el boxplot puede “marcar” muchos puntos no anómalos como valores atípicos. Hubert & Vandervieren (2008) propuso un ajuste al boxplot para resolver este problema: el boxplot ajustado por asimetría. Este boxplot corrige la asimetría utilizando una medida robusta en presencia de asimetría para determinar el “umbral” para los valores atípicos. Esto implica cambiar el límite de 1.5 la distancia intercuartílica por una medida corregida. Para un mayor detalle, ver Hubert & Vandervieren (2008).

Figura 2.3: Comparación del boxplot original y el ajustado según Hubert y Vandervieren (2008)

Fuente: elaboración propia.

2.3 Métricas para detectar outliers en una variable

Una aproximación complementaria a la aproximación gráfica para detectar anomalías univariadas es emplear estadísticas o métricas que permitan estandarizar los datos o construir “umbrales” o intervalos que sirvan como “fronteras” para determinar a partir de qué valor se determinará que una observación es o no anomalía. A continuación discutiremos 4 aproximaciones diferentes.

2.3.1 Uso de percentiles

Un método utilizado para la detección de valores atípicos se basa en los percentiles. Para este método, todas las observaciones que se encuentren fuera del intervalo formado por los percentiles \(2.5\) y \(97.5\) se considerarán posibles valores atípicos. Dependiendo del caso, también se pueden considerar otros percentiles como límites para construir el intervalo; por ejemplo, los percentiles \(1\) y \(99\), o \(5\) y \(95\).

Un gran problema de este método es que siempre encontraremos outliers con esta aproximación, pues siempre podremos encontrar las observaciones menores al percentil 1 y al percentil 99. Por ejemplo, si se cuenta con 100 observaciones, una observación siempre estará por debajo del primer percentil y otra estará por encima del percentil 99. Esto no necesariamente implica que estas observaciones sean atípicas. Esta aproximación tendrá que ser empleada con mucho cuidado.

2.3.2 Z-score

El z-score, también conocido como puntaje Z o índice de desviación estándar, es una medida estadística que nos permite comparar una observación con la media y la desviación estándar de la muestra. Es decir, el z-score estandariza los datos restándole la media (\(\bar X\)) y dividiéndolos por la desviación estándar (\(S\)). De esta manera, las puntuaciones z son el número de desviaciones estándar por encima y por debajo de la media de cada valor.

Formalmente el puntaje z para la observación \(i\) de la variable \(X\) es: \[\begin{equation} Z_i=\frac{X_i-\bar X}{S} \tag{2.1} \end{equation}\]

Cuanto más se aleja de cero la puntuación z de una observación, más inusual es. Un valor de corte “estándar” para encontrar valores atípicos es las puntuaciones Z mayores que 3 y menores que -3. Este umbral tiene origen en la distribución normal, en la que se espera que más allá de tres desviaciones estándar solo se encuentren 0.27% de las observaciones. Es decir, si los datos vienen de una distribución normal, es poco probable obtener una observación con un z-score mayor en valor absoluto que 3.

Sin embargo, si los datos no siguen la distribución normal, esta aproximación podría no ser conveniente. Por otro lado, la misma presencia del valor atípico distorsiona las puntuaciones z, ya que infla la media y la desviación estándar. En otras palabras, si una muestra contiene valores atípicos, los valores z están sesgados de tal forma que parecen ser menos extremos (más cercanos a cero).

2.3.3 Rango intecuartílico

La prueba de Tukey, también conocida como el método de los “bigotes” o el criterio del rango intercuartílico, es una técnica estadística utilizada para identificar valores atípicos en una variable o característica (datos univariados). Funciona creando un intervalo empleando la distancia entre el primer y tercer cuartil de los datos (rango intercuartílico) (IQR). El intervalo se construye restándole al primer cuartil (\(q_{0.25}\)) 1.5 veces la IRQ y sumándole al tercer cuartil (\(q_{0.75}\)) 1.5 veces la IQR. Si un valor está por fuera del intervalo, se considera un outlier.

En otras palabras, el intervalo \(I_T\) para esta prueba se construye de la siguiente manera:

\[\begin{equation} I_T =[q_{0.25}-1.5 IQR ; q_{0.75}+1.5 IQR ] \tag{2.2} \end{equation}\]

Así, cualquier valor por encima del límite superior es considerado un outlier; de manera similar, las observaciones por debajo del límite inferior son consideradas outliers. La prueba de Tukey es útil para identificar valores atípicos en un conjunto de datos de manera rápida y corresponde al mismo análisis que se realizaría empleando un boxplot.

2.3.4 Método de Hampel

El método de Hampel²³ (en inglés se conoce como Hampel Outlier Threshold) es un método estadístico no paramétrico para la detección de outliers que se basa en la idea de comparar cada observación con sus vecinos más cercanos. Los puntos de datos que se desvían sustancialmente de sus vecinos se identifican como outliers. Para identificar si la desviación a los vecinos es grande se crea el intervalo \(I_H\): \[\begin{equation} I_{H} = [median - k \cdot MAD; median + k \cdot MAD] \tag{2.3} \end{equation}\] donde \(MAD\) corresponde a la desviación absoluta de la mediana (Median Absolute Deviation en inglés) que se define como la mediana de las desviaciones absolutas con respecto a la mediana de los datos (\(\tilde{X}\)). Es decir, \[\begin{equation} MAD = median(|X_i - \tilde{X}|) \tag{2.4} \end{equation}\] Típicamente, se emplea \(k=3\) en (2.3) siguiendo la denominada regla de Pearson²⁴. En últimas \(k\) es un factor que determina la sensibilidad del método a los outliers. Si \(k\) es demasiado pequeño, esto puede conducir a la detección de muchos outliers; mientras que si \(k\) es muy grande puede que no se encuentren outliers.

2.3.5 Metricas que emplean estimadores robusto de varianza

Otra forma de encontrar outliers es crear umbrales o puntos de corte que empleen estimadores de varianza y media robustos a la presencia de valores atípicos. En este caso, el primer paso es encontrar una medida robusta de la raíz cuadrada media (\(RRMS\) por el término robust root mean square). En general la raíz cuadrada media (\(RMS\)) para una variable \(X_i\) se define como:

\[\begin{equation} RMS = \sqrt{\bar{X}^2 + S^2} \tag{2.5} \end{equation}\] donde \(\bar{X}\) representa la media y \(S^2\) es la varianza. La raíz cuadrada media (\(RMS\)), también conocida como valor cuadrático medio o valor eficaz, es una estadística descriptiva de volatilidad que permite calcular la variación promedio.

Por otro lado, recordemos que la existencia de valores atípicos implica que la media y la varianza se verán afectadas por esos valores atípicos. La \(RRMS\) emplea estimadores robustos de la tendencia central y de la varianza para mitigar el impacto de los valores atípicos en la media y varianza. Así, el \(RRMS\) será: \[\begin{equation} RRMS = \sqrt{ med(X)^2 + est.var(X)} \tag{2.6} \end{equation}\] donde \(med(X)\) es la mediana y \(est.var(X)\) es un estimador robusto para la varianza. Por ejemplo, el \(est.var(X)\) puede ser la desviación absoluta de la mediana (\(MAD\)) como se define en (2.4).

Empleando el \(RRMS\) se pueden escalar los datos²⁵ y así poderlos comparar con una distribución estadística. Así, podríamos discriminar entre los valores atípicos.

Esta aproximación implica construir un intervalo para los valores que no se consideran atípicos (como lo realizamos en las aproximaciones anteriores). En este caso el umbral superior estará dado por: \[\begin{equation} Umbral_{Superior} = med(X/RRMS) + F^{-1}(p) \cdot RRMS \tag{2.7} \end{equation}\] donde \(F()\) es una función de distribución acumulativa como por ejemplo la distribución t o normal. Así, \(F^{-1}()\) es la función cuantil. Y \(p\) es la probabilidad de \(F^{-1}()\) a partir de la cual deseamos definir el corte para los valores críticos. De manera similar se puede encontrar el umbral inferior. Así, una vez que se tienen los umbrales, podemos constatar que las observaciones superan dichos umbrales y, por tanto, se podrían catalogar como datos atípicos.

2.4 Empleando R para encontrar anomalías univariadas

En un EDA, inicialmente, los valores atípicos se pueden detectar evaluando los valores que son lógicamente imposibles. Por ejemplo, un ingreso para un cliente negativo. Para lograr identificar un outlier debemos comparar la observación con otras observaciones realizadas sobre el mismo fenómeno, pues es posible que la existencia misma del valor atípico pueda deberse a la variabilidad inherente al fenómeno que se observa. Adicionalmente, estas observaciones atípicas pueden aparecer debido a un error de medición o de codificación. Por tanto, es importante distinguir entre un outlier y un valor errado.

En esta sección implementaremos las métricas discutidas anteriormente en R. Para esto, emplearemos una base de datos de un banco comercial alemán que contiene información de clientes a los que se les ha otorgado un crédito y se han calificado como buenos o malos deudores. Los datos provienen de Hofmann (1994) y se encuentran en el archivo datos_credito.RData que se puede descargar de la página web del libro (https://www.icesi.edu.co/editorial/deteccion-anomalias). La base de datos contiene las siguientes variables:

edad (numérica) = edad,
residente (numérica) = años que lleva residiendo en Alemania,
propiedad.hogar = con las siguientes categorías: “rent”, “own”,“for free”,
trabajo = con las siguientes categorías: “unemployed/ unskilled - non-resident”, “unskilled - resident”,“skilled employee / official”, “management/ self-employed/”, “highly qualified employee/ officer”,
dependientes (numérica)= número de personas que dependen del cliente
trabajador.extranjero = trabajador extranjero con las siguientes categorías: “yes”, “no”,
empleado = tiempo que lleva empleado con las siguientes categorías: “unemployed”, “less than 1 year”, “equal or more than 1 and less than 4 years”,” equal or more than 4 and less than 7 years”, “equeal or more than 7 years”
estadocivil.genero = con las siguientes categorías: “male: divorced/separated”, “female: divorced/separated/married”, “male: single”, “male: married/widowed”, “female: single”.

Por otro lado, se cuenta con las siguientes variables relacionadas con el banco:

numero.creditos (numérica) = número de créditos existentes con el banco,
porcentage.disponible (numérica)= porcentaje del ingreso disponible para pagar cuotas de créditos,
cuenta.corriente (numérica)= estado de la cuenta corriente actual con categoría de respuesta: “less than 0 DM”, “0 or less than 200 DM”, “equal or greater than 200 DM / salary assignments for at least 1 year”, “no checking account”,
proposito.credito: propósito del crédito con las siguientes categorías de respuesta: “car (new)”, “car (used)”, “furniture/equipment”,“radio/television”, “domestic appliances”, “repairs”, “education”, “vacation”, “retraining”, “business”, “others”,
monto.credito (numérica) = monto del crédito,
cuenta.ahorros = estado de la cuenta de ahorros con las siguientes categorías: “less than 100 DM”, “equal or greater than 100 and less than 500 DM”, “equal or greater than 500 and less than 1000 DM”, “greater than 1000 DM”, “unknown/no savings account”.

Finalmente, se cuenta con la variable:

historial.crediticio = con categorías de respuestas: “no credits taken/ all credits paid back duly”, “all credits at this bank paid back duly”, “existing credits paid back duly till now”, “delay in paying off in the past”, “critical account/ other credits existing (not at this bank)”.

Carguemos los datos:

load("./datos/datos_credito.RData")

Los datos están cargados en el objeto de clase data.frame que denominamos german. Ese objeto tiene 14 variables y 1000 clientes. Miremos rápidamente los datos cargados empleando la función glimpse() del paquete dplyr (Wickham et al., 2021).

library(dplyr)
glimpse(german)

## Rows: 1,000
## Columns: 14
## $ cuenta.corriente      <fct> less than 0 DM, 0 or less than 200 DM, no checki…
## $ historial.crediticio  <fct> critical account/ other credits existing (not at…
## $ proposito             <fct> radio/television, radio/television, education, f…
## $ monto.credito         <int> 1169, 5951, 2096, 7882, 4870, 9055, 2835, 6948, …
## $ cuenta.ahorros        <fct> unknown/ no savings account, less than 100 DM, l…
## $ porcentaje.disponible <int> 4, 2, 2, 2, 3, 2, 3, 2, 2, 4, 3, 3, 1, 4, 2, 4, …
## $ estadocivil.sexo      <fct> male : single, female : divorced/separated/marri…
## $ residente             <int> 4, 2, 3, 4, 4, 4, 4, 2, 4, 2, 1, 4, 1, 4, 4, 2, …
## $ edad                  <int> 67, 22, 49, 45, 53, 35, 53, 35, 61, 28, 25, 24, …
## $ propiedad.hogar       <fct> own, own, own, for free, for free, for free, own…
## $ numero.creditos       <int> 2, 1, 1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, …
## $ ocupacion             <fct> skilled employee / official, skilled employee / …
## $ dependientes          <int> 1, 1, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
## $ trabajador.extranjero <fct> yes, yes, yes, yes, yes, yes, yes, yes, yes, yes…

Los datos han sido cargados satisfactoriamente, y la clase de cada variable concuerda con su descripción. Ahora procedamos a realizar el EDA.

2.4.1 Graficandolos datos

Empecemos nuestro análisis graficando los datos y para hacer el ejercicio más ágil, concentremos nuestra atención en la variable monto.credito²⁶.

Inicialmente, vamos a recurrir a los histogramas para detectar valores atípicos. Empleemos el paquete ggplot2 (Wickham, 2016) para construir el histograma²⁷.

source = "Cálculos propios."
library(ggplot2)

german %>% 
ggplot(  aes(x = monto.credito)) +
  geom_histogram(
    bins = round(sqrt(length(german$monto.credito))), 
    fill = "steelblue", color = "steelblue", alpha = 0.5
  ) +  xlab("Monto de crédito (DM)") + ylab("número de clientes") +
  theme_minimal()

Figura 2.4: Histograma de la variable Monto de crédito

Fuente: elaboración propia.

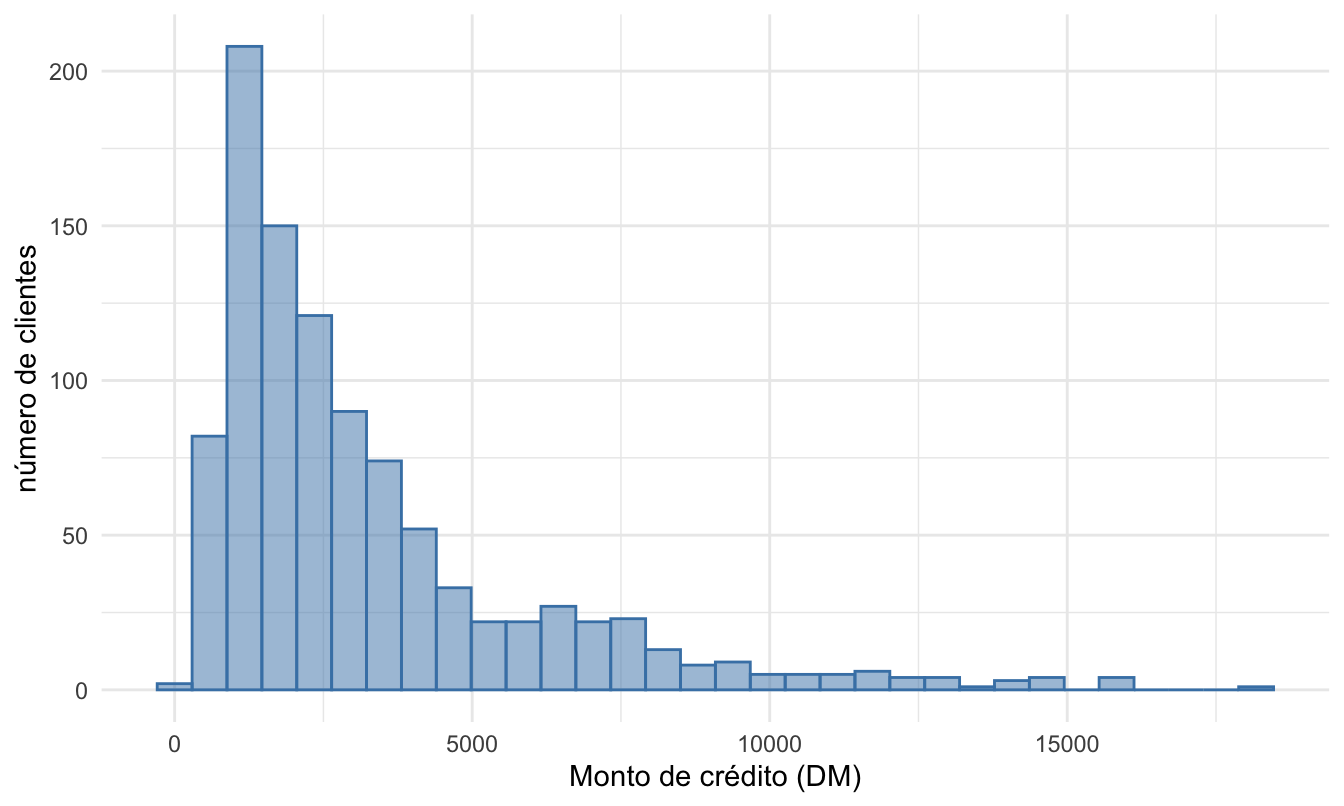
En el histograma vemos que existen unas observaciones de montos de créditos por encima de los 15 mil DM, relativamente grandes con respecto a las demás observaciones de los demás clientes (Ver las barras en el lado derecho de la Figura 2.4). Esto ya nos da unas sospechas de la existencia de valores atípicos (univariados) en esta variable. También podemos ver que los datos presentan asimetría positiva o sesgo a la derecha²⁸.

Ahora construyamos el respectivo boxplot empleando el paquete ggplot2 (Wickham, 2016)²⁹. El código que genera la Figura 2.5 es el siguiente:

german %>% 
ggplot( aes(x = monto.credito) )+
  geom_boxplot(fill = "steelblue", 
               outlier.colour = "blue", 
               alpha= 0.5, 
               color= "steelblue") + 
    xlab("Monto de crédito (DM)") + 
    ylab("") +
    theme_minimal() +
    theme(  axis.text.y=element_blank(),
      axis.ticks=element_blank(),
      axis.title.y=element_blank())

Figura 2.5: Boxplot de la variable Monto de crédito

Fuente: elaboración propia.

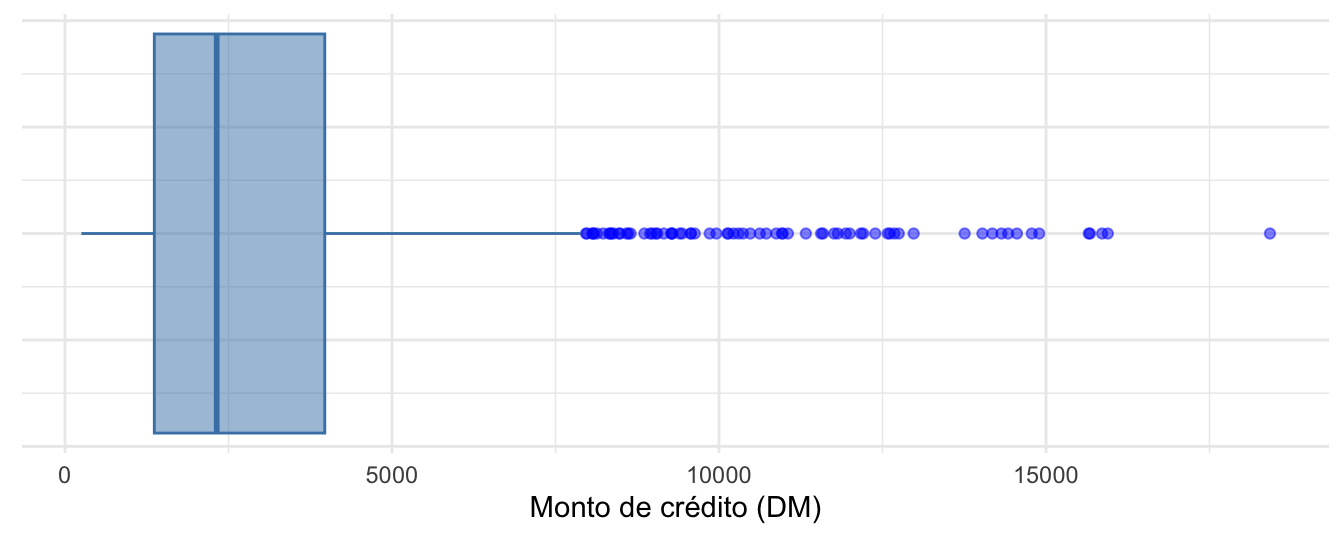
Como se discutió anteriormente, el gráfico de caja y bigotes permite visualizar una variable cuantitativa y permite mostrar estadísticas resumen tales como: mínimo, mediana, primer (\(q_{0.25}\)) y tercer (\(q_{0.75}\)) cuartil, máximo y cualquier observación que se clasifique como un valor atípico sospechoso utilizando el criterio de rango intercuartil (\(IQR\)).

En este caso, los datos atípicos parecen muchos (Ver puntos azules en la Figura 2.5); son 72 observaciones³⁰. Recordemos que este resultado puede estar influenciado por la asimetría de la distribución.

Siguiendo a Hubert & Vandervieren (2008) podemos ajustar al boxplot para resolver este problema. Esto lo podemos realizar empleando la función adjbox() del paquete robustbase (Maechler et al., 2024). Esta función solo necesita como argumento la variable a la que se le generará el boxplot ajustado. Así el boxplot ajustado se puede crear empleando el siguiente código:

# Crear boxplot ajustado según Hubert y Vandervieren (2008)
adjbox(german$monto.credito)

Esta función genera un boxplot ajustado empleando la base de R. Con un poco más de trabajo y empleando la función adjbox_stats() del mismo paquete robustbase podemos construir un boxplot ajustado empleando el paquete ggplot2. El siguiente código genera la Figura 2.6.

library(robustbase)
library(ggplot2)

adjbox_stats <- adjboxStats(german$monto.credito)$stats


ggplot(data.frame(german$monto.credito ), 
       aes(x= german.monto.credito, y = "")) + 
      geom_boxplot(xmin = adjbox_stats[1],
                     xmax = adjbox_stats[5],
                     middle = adjbox_stats[3],
                     upper = adjbox_stats[4],
                     lower = adjbox_stats[2],
                     outlier.shape = NA, 
                     fill = "steelblue", 
                     outlier.colour = "blue", 
                     alpha= 0.5, color= "steelblue") +
    geom_point(data=subset(data.frame(german$monto.credito),
                               german.monto.credito < adjbox_stats[1] | german.monto.credito > adjbox_stats[5]),
                   col = "blue", size = 2, 
                   shape = 16, alpha= 0.5) +
  xlab("Monto de crédito (DM)") + ylab("") +  
  theme_minimal() +
  theme(axis.text.y=element_blank(),
        axis.ticks=element_blank(),
        axis.title.y=element_blank())

Figura 2.6: Boxplot ajustado según Hubert y Vandervieren (2008) para la variable Monto de crédito

Fuente: elaboración propia.

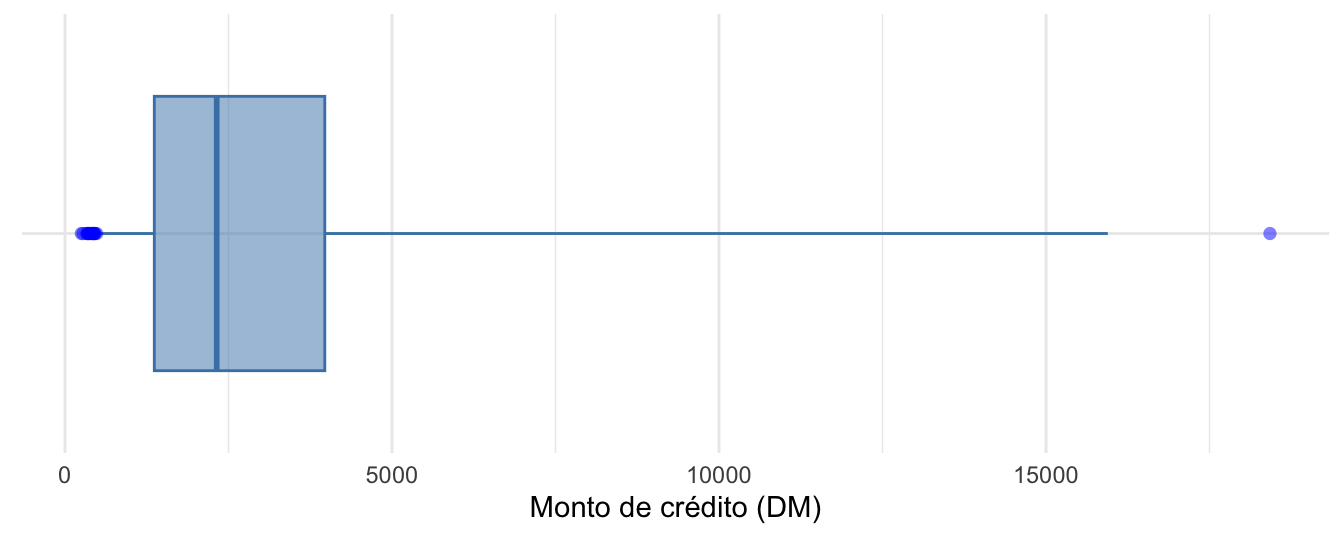
El boxplot ajustado muestra 19 datos atípicos tanto en la cola inferior como en la cola superior (Ver puntos azules en la Figura 2.6). De hecho, solo se encuentra un solo outlier grande y el resto son valores bajos³¹.

2.4.2 Métricas para detectar outliers

Recurrir a la estadística descriptivas y a las gráficas de los datos permite descubrir múltiples aspectos en estos tales como: patrones y en algunas ocasiones outliers. Sin embargo, es necesario recurrir a métricas o estadísticas que permitan estandarizar los datos o construir “umbrales” o intervalos que sirvan como “fronteras” para determinar a partir de qué valor se determinará que una observación es o no atípica. A continuación estudiaremos cómo implementar en R las cuatro métricas discutidas anteriormente.

Para calcular las estadísticas descriptivas hay varias opciones. Por ejemplo, podemos calcular las estadísticas descriptivas, variable por variable, con la función summary() de la base de R.

Por ejemplo,

summary(german$monto.credito)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##     250    1366    2320    3271    3972   18424

Otra opción para calcular las estadísticas descriptivas de una variable es emplear la función describe() del paquete psych (William Revelle, 2023). Por ejemplo:

#install.packages("psych")
library(psych) 
psych::describe(german$monto.credito)

##    vars    n    mean      sd median trimmed     mad min   max range skew
## X1    1 1000 3271.26 2822.74 2319.5 2754.57 1627.15 250 18424 18174 1.94
##    kurtosis    se
## X1     4.25 89.26

Nota que después de la mediana se presenta una estadística descriptiva que se denomina “trimmed”. Esta corresponde a la media truncada; es decir, es la media si se descartan un porcentaje de los datos más altos y de los más bajos. En el caso de la función describe(), del paquete psych, por defecto calcula la media truncada descartando el 10 % superior e inferior de los datos (el 5% más bajo y el 5% más alto). Comparando la media y la media truncada, puede evidenciarse una diferencia relativamente grande entre ellas, mostrando la posible existencia de valores anormalmente grandes. Si se quisiera recortar una proporción diferente, se puede hacer empleando el argumento trim de esa función. Por ejemplo, si se desea recortar solo el 5% de los datos extremos, el código sería:

psych::describe(german$monto.credito, trim= 0.05)

Puedes constatar que la media, truncando el 30% de las observaciones (15% más altas y 15% más bajas), es de 2387.23. Y si se recorta el 20%, es 2495.12. Estos dos números son diferentes pero no tanto como ocurre en el caso en que se elimina solo el 10% de los datos, 2754.57. Claramente hay unos datos anormalmente altos que jalonan la media.

2.4.2.1 Usando percentiles

Encontrar las observaciones que superan (o están por debajo de) un percentil se puede hacer fácilmente empleando el paquete dplyr y la función quantile() de la base de R. Supongamos que queremos detectar cuáles son los montos de crédito más altos. En especial queremos encontrar los clientes tal que el 99.5% de los clientes tengan montos de crédito inferiores. Esto se puede hacer de la siguiente manera³²:

german %>% 
  select(monto.credito) %>% 
filter(monto.credito > quantile(monto.credito, 0.995))

##   monto.credito
## 1         15945
## 2         15653
## 3         15857
## 4         15672
## 5         18424

Nota que por construcción, dado que tenemos 1000 observaciones, las observaciones que están por encima del percentil 99.5 serán 5.

2.4.2.2 z-score

El z-score para cada observación para un feature no es más que el resultado de estandarizar la variable. Esto se puede realizar empleando la función scale() de la base de R. El siguiente código produce los z-scores para la variable monto.credito para cada observación:

z_scores <- as.data.frame(scale(german$monto.credito))
names(z_scores) <- "score"

Y podemos encontrar las observaciones que tengan un z-score menor a -3 de la siguiente manera:

z_scores %>% 
  filter(score < -3)

## [1] score
## <0 rows> (or 0-length row.names)

Como se puede observar, no se encuentran valores atípicamente bajos con esta aproximación. De hecho, esto no es una sorpresa, pues el z-score tiene en mente una variable que provenga de una distribución normal (simétrica), lo cual no es lo adecuado para nuestro caso.

De manera similar, encontramos las observaciones con puntaje z por encima de 3.

out_obs <- z_scores %>% 
  filter(score > 3)

dim(out_obs)

## [1] 25  1

En este caso encontramos 25 observaciones cuyo puntaje z supera el umbral de 3. Nuevamente, esto parece algo excesivo.

2.4.2.3 Rango intercuartílico

Recordemos que el criterio IQR para detectar datos anómalos implica marcar todas las observaciones por encima de \(q_{0.75}+1.5 IQR\) o por debajo de \(q_{0.25}-1.5 IQR\) como valores atípicos (Ver puntos azules en la Figura 2.5).

Es posible extraer los valores de los posibles valores atípicos que se graficaron en el boxplot (Ver Figura 2.5 empleando la función boxplot.stats() del paquete grDevices (R Core Team, 2023). La función típicamente incluye los siguientes dos argumentos:

boxplot.stats(x, coef = 1.5)

donde:

x: Un vector de clase numeric que contiene las observaciones graficadas en el boxplot.
coef: corresponde a la extensión de los “bigotes” del boxplot en términos del \(IQR\). Por defecto, coef = 1.5. Es decir, se emplea 1.5 veces la distancia intercuartílica.

Esta función provee varios resultados importantes para construir la gráfica del boxplot que son guardados en diferentes compartimientos (slots); entre los cuales se destaca el slot out en el que se guardan los valores que se encuentran por encima de \(q_{0.75}+1.5 IQR\) o por debajo de \(q_{0.25}-1.5 IQR\). En nuestro caso, los valores de los outliers de la variable monto.credito pueden ser encontrados con el siguiente código:

#install.packages("grDevices")
library(grDevices)

boxplot.stats(german$monto.credito)$out

##  [1]  9055  8072 12579  9566 14421  8133  9436 12612 15945 11938  8487 10144
## [13]  8613  9572 10623 10961 14555  8978 12169 11998 10722  9398  9960 10127
## [25] 11590 13756 14782 14318 12976 11760  8648  8471 11328 11054  8318  9034
## [37]  8588  7966  8858 12389 12204  9157 15653  7980  8086 10222 10366  9857
## [49] 14027 11560 14179 12680  8065  9271  9283  9629 15857  8335 11816 10875
## [61]  9277 15672  8947 10477 18424 14896 12749 10297  8358 10974  8386  8229

Recurriendo al uso de la función which() es posible obtener el número de la fila correspondiente a los valores atípicos; es decir el número de la observación. En este caso el código es:

out <- boxplot.stats(german$monto.credito)$out
out_ind <- which(german$monto.credito %in% c(out))
out_ind

##  [1]   6  18  19  58  64  71  79  88  96 106 131 135 137 181 206 227 237 269 273
## [20] 275 286 292 296 305 334 374 375 379 382 396 403 418 432 451 492 497 510 526
## [39] 550 564 616 617 638 646 654 658 673 685 715 737 745 764 772 806 809 813 819
## [58] 829 833 855 882 888 896 903 916 918 922 928 946 954 981 984

Con esta información, es posible volver fácilmente a las filas específicas del conjunto de datos para verificarlas o imprimir todas las variables para estos valores atípicos. Según el método, se tiene un total de 72 observaciones atípicas.

out_dataset<-german[out_ind,]

Por otro lado, recordemos que esta aproximación puede generar muchos valores atípicos en presencia de una muestra con sesgo. En la Figura 2.6 aplicamos la técnica propuesta por Hubert & Vandervieren (2008) para ajustar el boxplot a muestras con sesgo. En ese caso encontramos 19 datos atípicos tanto en la cola inferior como en la cola superior (Ver puntos azules en la Figura 2.6).

Para conocer los valores de las observaciones que se considerarían outliers con este ajuste (rango intercuartílico ajustado) lo podemos hacer con la función adjboxStats() del paquete robustbase (Wickham et al., 2021). Esta función es muy similar a la función boxplot.stats() que acabamos de emplear. En este caso solo necesitamos un argumento: los datos que se grafican en el boxplot. El siguiente código permite encontrar los valores de las observaciones atípicas empleando la corrección de Hubert & Vandervieren (2008):

adjboxStats(german$monto.credito)$out

##  [1]   426   409   458   392   339   338   433   276   362   343   448   368
## [13]   385   433   250   428   484 18424   454

De manera similar a lo que hicimos con la \(IRQ\) sin ajuste, es posible obtener el número de la fila correspondiente a los valores atípicos con el siguiente código:

out <- adjboxStats(german$monto.credito)$out
out_ind <- which(german$monto.credito %in% c(out))
out_ind

##  [1]  27  28  40 112 158 178 250 310 380 459 472 494 591 722 726 751 812 916 965

Otra forma de aplicar esta aproximación es empleando la función *tukey_outlier()** del paquete funModeling (Casas, 2024). Tú puedes mirar en la ayuda cómo emplear esta función.

2.4.3 Método de Hampel

El método de Hampel se puede implementar en R con el paquete funModeling (Casas, 2024) y la función hampel_outlier(). Esta función solo necesita dos argumentos. El argumento input que corresponde al vector de datos cuantitativos y el argumento k_mad_value que corresponde al multiplicador de la desviación absoluta mediana; es decir, \(k\) en la expresión (2.3). El valor por defecto de este segundo argumento es k_mad_value = 3 (\(k=3\)).

El siguiente código genera los umbrales de Hampel (Ver expresión (2.3)) para la variable monto.credito:

# install.packages("funModeling")

# Cargar el paquete
library(funModeling)

h_outliers <- hampel_outlier(input = german$monto.credito)
h_outliers

## bottom_threshold    top_threshold 
##         -2561.96          7200.96

El siguiente código permite identificar el número de las observaciones que no se encuentran en el intervalo de Hampel; es decir, las que superan el umbral para la variable monto.credito y por tanto se consideran outliers:

out_ind <- which(german$monto.credito <  h_outliers[1] | german$monto.credito >  h_outliers[2])
out_ind

##   [1]   4   6  18  19  49  58  64  71  79  88  96 106 109 114 131 135 137 154
##  [19] 164 176 181 206 227 228 237 256 269 273 275 286 288 292 295 296 305 333
##  [37] 334 374 375 376 379 382 388 396 403 412 418 432 451 468 492 497 510 526
##  [55] 539 550 564 616 617 638 646 651 654 658 673 685 715 716 737 745 764 772
##  [73] 797 805 806 809 813 816 819 829 833 855 869 871 881 882 888 890 896 903
##  [91] 916 918 922 928 946 954 972 974 981 984

En este caso se encuentran 100 observaciones marcadas como outliers por el método de Hampel. Y con el siguiente código podemos ver los valores de dichas observaciones para la variable monto.credito:

out_obs <- german$monto.credito[out_ind]
out_obs

2.4.4 Métricas que emplean estimadores robusto de varianza

El paquete hotspots (Darrouzet-Nardi, 2018) permite identificar valores atípicos empleando estimadores robustos a la presencia de datos atípicos para la media (mediana) y la varianza (\(MAD\)) y comparándolos con lo esperado con una distribución (como la distribución t y normal).

La función outliers() del paquete hotspots permite hacer esta tarea rápidamente. Esta función típicamente incluye los siguientes argumentos:

outliers(x, p, tail, distribution, var.est = “mad”)

donde:

x: Un vector de clase numeric que contiene las observaciones de la variable de interés.
p: probabilidad para calcular el punto de corte (entre 0 y 1). El valor por defecto de este argumento es p = 0.99.
tail: determina si los límites se calculan para la cola superior (“positive”), inferior (negative) o ambas (“both”. Por defecto es “positivo”, pero también puede ser “negativo” o “ambos”. El valor por defecto es tail = “positive”.
distribution: Función de distribución que se empleará para calcular el umbral para determinar los valores atípicos. Por defecto, este argumento será distribution = “t”. El otro posible valor es “normal”.

Por ejemplo, empleando la distribución t para construir tanto el umbral inferior como superior el código será

library(hotspots)
out_mad<-hotspots::outliers(german$monto.credito, tail = "both")
out_mad

## outlier cutoff (positive): 
## [1] 6711.865
## outlier cutoff (negative): 
## [1] -2072.865

Los resultados se pueden resumir empleando la función summary() de la siguiente manera:

summary(out_mad)

## 
## Source data: german$monto.credito
## Distribution and probability: t, 0.99
## Tail: positive and negative outliers                           
## Mean:             3.271e+03
## Median:           2.320e+03
## Min:              2.500e+02
## Max:              1.842e+04
## mad:              1.627e+03
## CV (mad/median):  7.015e-01
## 
## n =  1000
## 
## positive outliers:
##   Cutoff  number positive outliers  % positive outliers   % sum
##     6712                       117                  11.7   34.1
## 
## 
## negative outliers:
##   Cutoff  number negative outliers  % negativeoutliers   % sum
##    -2073                         0                    0      0

Esta aproximación encuentra 117 outliers en la parte superior y ninguno en la parte inferior. Estos se pueden visualizar empleando la función plot(), de la siguiente manera:

plot(out_mad)

Figura 2.7: Observaciones atípicas (en rojo) con estimador robusto para la varianza y comparando con una distribución t (p = 0.99)

Fuente: elaboración propia.

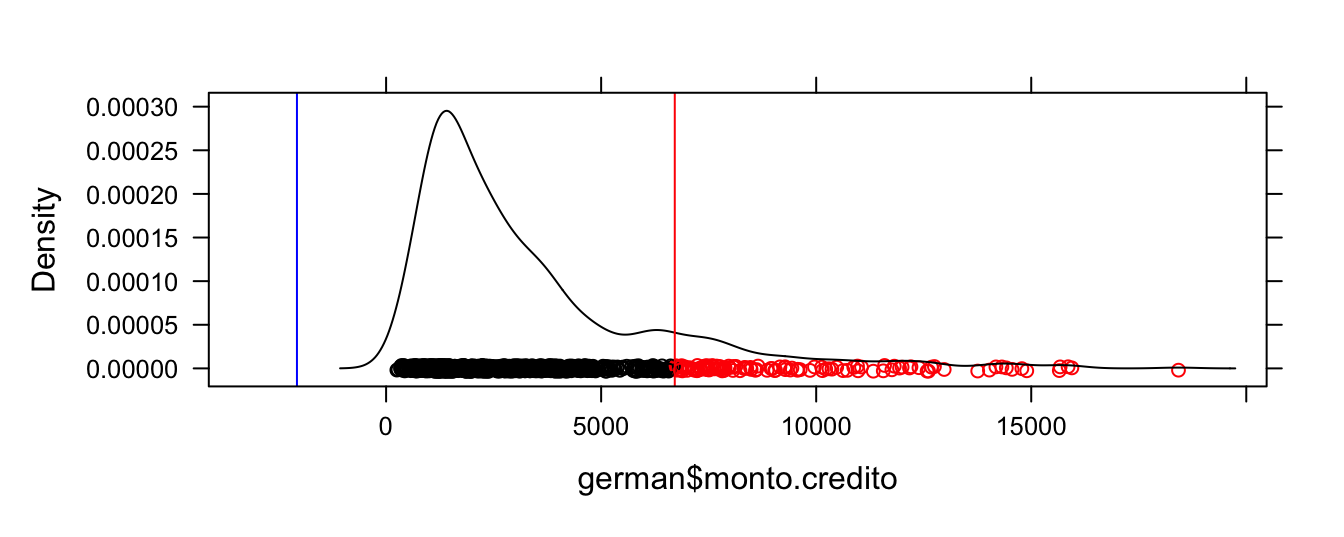
Las observaciones atípicas las podemos obtener de manera similar a como las hemos encontrado en las subsecciones anteriores. En este caso el código sería:

# posición de los outliers
out_ind <- which(german$monto.credito <  out_mad$negative.cut | german$monto.credito > out_mad$positive.cut)
out_ind

##   [1]   4   6   8  18  19  30  49  58  64  71  79  88  96 100 106 109 114 117
##  [19] 131 132 135 137 154 155 164 176 181 206 227 228 237 256 269 273 275 286
##  [37] 288 292 295 296 305 333 334 374 375 376 379 382 388 396 403 412 418 432
##  [55] 451 468 492 497 508 510 518 523 526 539 550 553 564 570 616 617 638 646
##  [73] 651 654 658 673 685 715 716 737 739 745 764 772 797 805 806 809 813 816
##  [91] 819 829 833 847 855 869 871 880 881 882 888 890 896 903 916 918 922 925
## [109] 928 940 946 954 969 972 974 981 984

# valores atípicos
out_obs <- german$monto.credito[out_ind]
out_obs

##   [1]  7882  9055  6948  8072 12579  6836  7228  9566 14421  8133  9436 12612
##  [13] 15945  7057 11938  7721  7855  7174  8487  6887 10144  8613  7758  6967
##  [25]  7308  7485  9572 10623 10961  7865 14555  7418  8978 12169 11998 10722
##  [37]  7582  9398  7629  9960 10127  7408 11590 13756 14782  7685 14318 12976
##  [49]  7374 11760  8648  7253  8471 11328 11054  7238  8318  9034  6850  8588
##  [61]  7127  7119  7966  7763  8858  6999 12389  6758 12204  9157 15653  7980
##  [73]  7476  8086 10222 10366  9857 14027  7596 11560  6761 14179 12680  8065
##  [85]  7511  7472  9271  9283  9629  7432 15857  8335 11816  6761 10875  7409
##  [97]  7678  6742  7814  9277 15672  7824  8947 10477 18424 14896 12749  6872
## [109] 10297  6842  8358 10974  7166  7393  7297  8386  8229

Antes de continuar nuestro estudio, es importante mencionar que el paquete univOutl (D’Orazio, 2022), provee una “infraestructura” que permite implementar casi todos los métodos estudiados en este capítulo. Por ejemplo, la función boxB() permite implementar el método del rango intercuartílico, sin y con el ajuste por distribuciones asimétricas de Hubert & Vandervieren (2008). La función típicamente incluye los siguientes argumentos:

boxB(x, k, method)

donde:

x: Un vector de clase numeric que contiene las observaciones de la variable de interés.
k: Constante no negativa que determina la extensión de los ‘bigotes’. El valor por defecto es 1.5.
method: Determina el método que se va a emplear. La opción method=“resistant” corresponde a la aproximación tradicional y method=“adjbox” implica emplear el boxplot ajustado de Hubert & Vandervieren (2008) para distribuciones sesgadas.

#install.packages("univOutl")
library(univOutl)
boxB(german$monto.credito, k = 1.5, method = 'resistant')

## $quartiles
##     25%     50%     75% 
## 1365.50 2319.50 3972.25 
## 
## $fences
##     lower     upper 
## -2544.625  7882.375 
## 
## $excluded
## integer(0)
## 
## $outliers
##  [1]   6  18  19  58  64  71  79  88  96 106 131 135 137 181 206 227 237 269 273
## [20] 275 286 292 296 305 334 374 375 379 382 396 403 418 432 451 492 497 510 526
## [39] 550 564 616 617 638 646 654 658 673 685 715 737 745 764 772 806 809 813 819
## [58] 829 833 855 882 888 896 903 916 918 922 928 946 954 981 984
## 
## $lowOutl
## integer(0)
## 
## $upOutl
##  [1]   6  18  19  58  64  71  79  88  96 106 131 135 137 181 206 227 237 269 273
## [20] 275 286 292 296 305 334 374 375 379 382 396 403 418 432 451 492 497 510 526
## [39] 550 564 616 617 638 646 654 658 673 685 715 737 745 764 772 806 809 813 819
## [58] 829 833 855 882 888 896 903 916 918 922 928 946 954 981 984

boxB(german$monto.credito,  method = 'adjbox')

## $quartiles
##     25%     50%     75% 
## 1365.50 2319.50 3972.25 
## 
## $fences
##      lower      upper 
##   499.6755 16097.1160 
## 
## $excluded
## integer(0)
## 
## $outliers
##  [1]  27  28  40 112 158 178 250 310 380 459 472 494 591 722 726 751 812 916 965
## 
## $lowOutl
##  [1]  27  28  40 112 158 178 250 310 380 459 472 494 591 722 726 751 812 965
## 
## $upOutl
## [1] 916

En el mismo paquete podemos encontrar la función LocScaleB(), que puede identificar valores anómalos empleando el rango intercuartílico con un ajuste robusto para la varianza y media (method=‘IQR’)³³ y desviación media absoluta (\(MAD\)) sugerida por el método de Hampel (method=‘MAD’).

Veamos dos ejemplos que te permitirán entender cómo funciona esta función. El primer ejemplo emplea el método del rango intercuartílico con un ajuste robusto para la varianza y media y el segundo emplea el método de Hampel.

LocScaleB(german$monto.credito,  method='IQR')

## $pars
##   median    scale 
## 2319.500 1932.357 
## 
## $bounds
## lower.low  upper.up 
## -3477.572  8116.572 
## 
## $excluded
## integer(0)
## 
## $outliers
##  [1]   6  19  58  64  71  79  88  96 106 131 135 137 181 206 227 237 269 273 275
## [20] 286 292 296 305 334 374 375 379 382 396 403 418 432 451 492 497 510 550 564
## [39] 616 617 638 658 673 685 715 737 745 764 806 809 813 819 829 833 855 882 888
## [58] 896 903 916 918 922 928 946 954 981 984
## 
## $lowOutl
## integer(0)
## 
## $upOutl
##  [1]   6  19  58  64  71  79  88  96 106 131 135 137 181 206 227 237 269 273 275
## [20] 286 292 296 305 334 374 375 379 382 396 403 418 432 451 492 497 510 550 564
## [39] 616 617 638 658 673 685 715 737 745 764 806 809 813 819 829 833 855 882 888
## [58] 896 903 916 918 922 928 946 954 981 984

LocScaleB(german$monto.credito,  method='MAD')

## $pars
##   median    scale 
## 2319.500 1627.153 
## 
## $bounds
## lower.low  upper.up 
##  -2561.96   7200.96 
## 
## $excluded
## integer(0)
## 
## $outliers
##   [1]   4   6  18  19  49  58  64  71  79  88  96 106 109 114 131 135 137 154
##  [19] 164 176 181 206 227 228 237 256 269 273 275 286 288 292 295 296 305 333
##  [37] 334 374 375 376 379 382 388 396 403 412 418 432 451 468 492 497 510 526
##  [55] 539 550 564 616 617 638 646 651 654 658 673 685 715 716 737 745 764 772
##  [73] 797 805 806 809 813 816 819 829 833 855 869 871 881 882 888 890 896 903
##  [91] 916 918 922 928 946 954 972 974 981 984
## 
## $lowOutl
## integer(0)
## 
## $upOutl
##   [1]   4   6  18  19  49  58  64  71  79  88  96 106 109 114 131 135 137 154
##  [19] 164 176 181 206 227 228 237 256 269 273 275 286 288 292 295 296 305 333
##  [37] 334 374 375 376 379 382 388 396 403 412 418 432 451 468 492 497 510 526
##  [55] 539 550 564 616 617 638 646 651 654 658 673 685 715 716 737 745 764 772
##  [73] 797 805 806 809 813 816 819 829 833 855 869 871 881 882 888 890 896 903
##  [91] 916 918 922 928 946 954 972 974 981 984

2.5 Comentarios finales

Hasta el momento hemos estudiado cómo detectar anomalías univariadas (outliers) empleando herramientas de la estadística que se emplean en un EDA. Vimos cómo emplear histogramas, el boxplot y ajustar el boxplot para la existencia de asimetría en la distribución. También discutimos técnicas que implican construir umbrales para determinar qué observaciones son atípicas como:

Uso de percentiles
Rango intecuartílico (prueba de Tukey)
Método de Hampel

Así mismo, discutimos una aproximación que implica reescalar los datos para compararlos con umbrales de la distribución normal (z-score) y otra que implica emplear estimadores robustos a la presencia de valores atípicos para la varianza y media y posteriormente comparar los datos reescalados con una distribución.

Es importante anotar que solamente realizamos el análisis de una de las variables cuantitativas de la base de datos. Un EDA completo y un análisis de anomalías univariado completo implicarán replicar nuestro análisis para las otras variables cuantitativas. ¡Inténtalo!

La combinación de la aproximación gráfica y con métricas nos permite empezar a llenar nuestra caja de herramientas con técnicas estadísticas para detectar outliers (anomalías univariadas). En el Capítulo 3 estudiaremos pruebas estadísticas para detectar anomalías univariadas. En los Capítulo 4 y 5 estudiaremos aproximaciones estadísticas para detectar anomalías multivariadas. En estos capítulos seguiremos llenando nuestra caja de herramientas con aproximaciones para la detección de anomalías.

Referencias

Alonso, J. C. (2022). Empezando a transformar bases de datos con r y dplyr. Universidad Icesi. https://doi.org/10.18046/EUI/bda.h.2

Alonso, J. C. (2024). Introducción al modelo clásico de regresión para científico de datos en r. Universidad Icesi. https://doi.org/https://doi.org/10.18046/EUI/bda.h.4

Alonso, J. C., & Largo, M. F. (2023). Empezando a visualizar datos con r y ggplot2. (2. ed.). Universidad Icesi. https://doi.org/10.18046/EUI/bda.h.3.2

Casas, P. (2024). funModeling: Exploratory data analysis and data preparation tool-box. https://CRAN.R-project.org/package=funModeling

D’Orazio, M. (2022). univOutl: Detection of univariate outliers. https://CRAN.R-project.org/package=univOutl

Darrouzet-Nardi, A. (2018). Hotspots: Hot spots. https://CRAN.R-project.org/package=hotspots

Hampel, F. R. (1974). The influence curve and its role in robust estimation. Journal of the American Statistical Association, 69(346), 383–393.

Harrell, F. E., & Davis, C. E. (1982). A new distribution-free quantile estimator. Biometrika, 69(3), 635–640. https://doi.org/10.1093/biomet/69.3.635

Hofmann, H. (1994). Statlog (German Credit Data). UCI Machine Learning Repository.

Hubert, M., & Vandervieren, E. (2008). An adjusted boxplot for skewed distributions. Computational Statistics & Data Analysis, 52(12), 5186–5201.

Maechler, M., Rousseeuw, P., Croux, C., Todorov, V., Ruckstuhl, A., Salibian-Barrera, M., Verbeke, T., Koller, M., Conceicao, E. L. T., & Anna di Palma, M. (2024). Robustbase: Basic robust statistics. http://robustbase.r-forge.r-project.org/

R Core Team. (2023). R: A language and environment for statistical computing. R Foundation for Statistical Computing. https://www.R-project.org/

Tukey, J. W. (1970). Exploratory data analysis - preliminary edition. Addison-Wesley.

Tukey, J. W. (1977). Exploratory data analysis (Vol. 2). Addison-Wesley Series in Behavioral Science: Quantitative Methods.

Wickham, H. (2016). ggplot2: Elegant graphics for data analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org

Wickham, H., François, R., Henry, L., & Müller, K. (2021). Dplyr: A grammar of data manipulation. https://CRAN.R-project.org/package=dplyr

William Revelle. (2023). Psych: Procedures for psychological, psychometric, and personality research. Northwestern University. https://CRAN.R-project.org/package=psych

Estos valores pueden ser causados por errores en la medición, fraude, eventos excepcionales o simplemente por la naturaleza de los datos.↩︎
Los outliers se pueden considerar como sinónimo de anomalía puntual: una observación individual que, bajo un modelo o métrica de referencia, presenta un grado de rareza extremo.↩︎
Si consideramos por separado cada variable para esa observación, la observación también será un outlier univariado (con respecto a las dos variables).↩︎
También conocidos como diagrama de cajas y bigotes.↩︎
Siete años después, Tukey publica el libro que se divulga ampliamente y populariza esta gráfica (Ver Tukey (1977))↩︎
Este gráfico también es conocido como el diagrama de cajas y bigotes.↩︎
Este método fue propuesto por Hampel (1974).↩︎
Esta regla también es conocida como la regla de Tukey-Pearson. La regla de Pearson se basa en la idea de comparar la distancia entre el punto de datos que se está evaluando y la mediana con la distribución de las distancias entre los puntos de datos dentro de la ventana.↩︎
Algo similar a lo que se desea hacer con el z-score, pero en este caso teniendo en cuenta que para la escalada necesitamos medidas robustas a la presencia de outliers.↩︎
En un EDA es necesario replicar el análisis que se presenta en esta sección a todas las demás variables. El análisis se debe realizar variable por variable. Por razones de espacio no realizamos dicho análisis en esta obra.↩︎
Para el detalle de cómo funciona el paquete y este gráfico puedes ver la sección 3.1 de Alonso & Largo (2023). Puedes acceder a esa sección con el siguiente enlace: https://www.icesi.edu.co/editorial/empezando-visualizar-2ed-web/dist.html#histograma.↩︎
Para una discusión sobre el tema puedes consultar la sección 15.6 de Alonso (2024) empleando el siguiente enlace: https://www.icesi.edu.co/editorial/modelo-clasico-web/Estadistica.html#varianza-y-momentos-alrededor-de-la-media-de-una-variable-aleatoria. ↩︎
Para el detalle de cómo funciona el paquete y esta gráfica puedes ver la sección 3.3 de Alonso & Largo (2023). Puedes acceder a esa sección con el siguiente enlace: https://www.icesi.edu.co/editorial/empezando-visualizar-2ed-web/dist.html#box.↩︎
En la Sección 2.4.2.3 veremos en detalle cómo encontrar las observaciones que corresponden a anomalías.↩︎
En la Sección 2.4.2.3 veremos en detalle cómo encontrar las observaciones que corresponden a anomalías empleando este boxplot ajustado.↩︎
Para entender cómo funciona el paquete dplyr y cómo se filtran observaciones, puedes consultar la Sección 2.1 de Alonso (2022). Ese documento lo puedes consultar en el siguiente enlace: https://www.icesi.edu.co/editorial/empezando-transformar-web/filtrar.html#filtrar-1.↩︎
Cuando se utiliza el argumento method=‘IQR’ se implementa una versión robusta del método tradicional de detección de valores atípicos basada en el rango intercuartílico que estudiamos previamente. En este caso, los cuantiles son calculados mediante técnicas de bootstrap o el método robusto propuesto por Harrell & Davis (1982). Para mayor detalle puedes consultar la ayuda de esta función.↩︎