4 Técnicas estadísticas para detectar outliers multivariados
4.1 Introducción
En el Capítulo 1, discutimos que existen diferentes tipos de anomalías y por tanto diferentes tipos de aproximaciones para su detección. En el Capítulo 2 estudiamos el uso de la aproximación gráfica (histogramas y boxplots) y el uso de métricas para “marcar” observaciones como posibles outliers. Las métricas que estudiamos fueron: percentiles, z-score, rango intercuartílico, método de Hampel y métricas que emplean estimadores robustos de varianza y media. En el Capítulo 3 estudiamos métodos de origen en la estadística para detectar anomalías univariadas con un determinado nivel de confianza, específicamente cuatro diferentes pruebas que permiten hacer inferencia estadística sobre la presencia o no de datos atípicos (outliers) en una variable; es decir, la existencia de anomalías univariadas39.
En este capítulo discutimos aproximaciones desde la estadística para detectar outliers multivariados. Así como en el caso de las anomalías univariadas, la estadística ha desarrollado métricas y pruebas para detectar outliers multivariados. En este capítulo y en este libro solo cubriremos las aproximaciones estadísticas que implican el cálculo de una métrica de distancia y la comparación de las métricas de las observaciones con un umbral para ser consideradas como valores atípicos. Más adelante en el Capítulo 5 estudiaremos una técnica matemática de reducción de dimensionalidad que es empleada en la estadística para la detección de outliers. Y posteriormente, en los capítulos 8 a 10 estudiaremos técnicas del aprendizaje de máquina que sirven para encontrar anomalías multivariadas.
4.2 Métricas basadas en distancias
Las medidas de distancia (o similitudes) nos permiten cuantificar la proximidad entre dos objetos estadísticos. Estos objetos pueden ser dos variables aleatorias, dos distribuciones de probabilidad o una observación frente a otras observaciones. Las distancias se emplean en muchas tareas de la analítica como en la tarea de clústering en que las medidas de similitud juegan un papel importante en determinar qué observaciones se parecen entre si y cuáles no40 y la tarea de clasificación en modelos como el kNN (k vecinos próximos) donde las medidas de distancia permiten escoger los vecinos más próximos41.
En la tarea de detección de anomalías, las medidas de distancia son una herramienta natural para medir qué tan cerca se encuentra una observación de otra. En especial son útiles para medir la cercanía entre observaciones cuando tenemos múltiples variables (features). Existen muchas medidas de distancia como la distancia euclidiana, la distancia de Chebyshev (también conocida como la distancia máxima), la distancia de Manhattan, la distancia de Canberra, la distancia de Minkowski y la distancia binaria (Ver sección 8.1 para una breve discusión de estas distancias42).
De todas las distancias, la más conocida y empleada es la distancia euclidiana. Desde el punto de vista geométrico, la distancia euclidiana entre dos observaciones es la distancia más corta posible entre ellas.
Formalmente, definamos el vector de las observaciones para las \(d\) variables para un individuo \(i\), como \(\mathbf{x_i}= [ x_{i,1} \quad x_{2,1} \quad \cdots \quad x_{i,d} ]\); en otras palabras, la \(i\)-ésima fila de la matriz de datos \(\textbf{X}_{n \times d}\). Entonces, la distancia euclidiana se define como:
\[\begin{equation} d(\mathbf{x_i},\mathbf{x_j}) = \sqrt{\left (\sum_{m = 1}^ {d} \left ( x_{i,m} - x_{j,m} \right)^{2} \right)}=\sqrt{ \left (\mathbf{x_i} - \mathbf{x_j} \right)^{T} \left ( \mathbf{x_i} -\mathbf{x_j} \right) } \tag{4.1} \end{equation}\]
Nota que para cada observación se puede calcular la distancia con respecto a las otras \(n-1\) observaciones, de tal manera que terminamos con \((n(n-1))/2\) pares de distancias.
4.2.1 Distancia de Mahalanobis
Un problema de la medida de distancia euclidiana es que no tiene en cuenta la correlación entre las variables. En caso de existir correlación entre las variables, la distancia euclidiana asigna el mismo peso a dichas variables y, puesto que estas variables miden esencialmente la misma característica, esta única característica recibe un peso adicional (Mclachlan, 1999).
Mahalanobis (1936) propuso una medida de distancia que resolviera este problema. La medida propuesta por el autor terminó tomando su apellido y hoy se conoce como la distancia Mahalanobis. La idea en esta distancia es escalar la contribución de las variables individuales con el valor de la distancia en función de la variabilidad de cada variable43. A diferencia de las distancias más conocidas como la euclidiana, en la que se asume independencia entre las variables, la distancia Mahalanobis usa la correlación entre las variables para ajustar su separación; este aspecto la hace muy útil en el caso en que el conjunto de datos tiene correlaciones entre sí.
La distancia de Mahalanobis se calcula para cada observación con respecto al centro de la distribución de datos; es decir, la media multivariada del conjunto de datos. De esta manera tendremos una distancia de Mahalanobis por cada observación. A diferencia de la distancia euclidiana que se calcula entre las parejas de observaciones.
Formalmente, la distancia de Mahalanobis para la \(i\)-ésima observación \(MD(\mathbf{x_i})\) se define como: \[\begin{equation} MD(\mathbf{x_i}) = \sqrt{(\mathbf{x_i} - \bar{\mathbf{X}})^T \Sigma^{-1} (\mathbf{x_i} - \bar{\mathbf{X}})} \tag{4.2} \end{equation}\] donde \(\bar{\mathbf{X}}\) corresponde al vector que contiene las medias para cada variable; es decir, la media de cada columna de la matriz \(\textbf{X}_{n \times d}\). Y finalmente, \[\begin{equation} \Sigma = \begin{bmatrix} S_1^2 & S_{1,2} & \cdots & S_{1,d} \\ S_{1,2} &S_2^2 & \cdots & S_{2,d} \\ \vdots & \vdots & \ddots & \vdots \\ S_{1,d} & S_{2,d} & \cdots &S_d^2 \\ \end{bmatrix} \tag{4.3} \end{equation}\] donde \(S_{k,l}\) es la covarianza entre la \(k\)-ésima variable (columna \(k\) de la matriz \(\textbf{X}_{n \times p}\)) y la \(l\)-ésima variable y \(S_k^2\) es la varianza de la \(k\)-ésima variable. No sobra enfatizar que mientras que la distancia euclidiana mide la distancia directa entre dos observaciones, la distancia de Mahalanobis mide qué tan lejos está una observación del centro de su distribución (multivariada), ajustando por la varianza y la covarianza de los datos.
Nota que en últimas, la distancia de Mahalanobis mide el número de desviaciones estándar que hay entre una observación y la media de una distribución. Por esta razón, la distancia Mahalanobis es muy empleada para la detección de múltiples valores atípicos (outliers) en variables cuantitativas.
Adicionalmente, se ha documentado que la distancia de Mahalanobis es menos sensible a la presencia de outliers en el conjunto de datos. Por otro lado, el cálculo de la distancia de Mahalanobis requiere la inversión de la matriz de varianzas y covarianza, lo que puede ser computacionalmente costoso para conjuntos de datos grandes.
Para identificar los valores atípicos, la distancia de Mahalanobis entre cada observación \(i\) y el centro en los datos de \(n\) dimensiones se necesita fijar un umbral. Algunos autores suelen fijarse arbitrariamente el umbral en 3 desviaciones estándar. Sin embargo, autores como P. J. Rousseeuw & Van Zomeren (1990) han demostrado que la distancia de Mahalanobis puede aproximarse mediante una distribución Chi-cuadrado (\(\chi^2\)) con \(d\) (el número de variables o features) grados de libertad. De esta manera, las observaciones con una distancia de Mahalanobis (\(MD(\mathbf{x_i})\)) mayor que \(\chi^2_{d,\alpha}\) serán marcadas como outliers por esta aproximación. Por otro lado, algunos autores como Cabana et al. (2021) sugieren emplear \(\alpha\) en 0,025; es decir, emplear el umbral en el 2,5% de observaciones más extremas.
4.2.2 Distancia robusta de Mahalanobis
En la Sección 2.3.5 discutimos cómo los estimadores tanto de la media como de la desviación estándar pueden tener problemas de sesgo en la presencia de outliers. La situación que observamos en el análisis univariado también está presente en el caso multivariado; y ahora se le suma el sesgo posible en la covarianza y por tanto en la correlación. Una solución natural es emplear estimadores robustos a la presencia de valores atípicos para resolver el problema, tal como lo realizamos en el caso univariado.
Autores como P. Rousseeuw & Zomeren (1990) propusieron emplear una distancia robusta de Mahalanobis. Esta propuesta implica sustituir los estimadores de los parámetros de la media (\(\bar{\mathbf{X}}\)) y la matriz de varianzas y covarianzas (\(\Sigma\)). Por ejemplo, P. Rousseeuw & Zomeren (1990) sugieren estimar esos parámetros a través del método elipsoide de volumen mínimo (MVE por las siglas en inglés). Otros autores como EStimator (1999) y P. Rousseeuw (1984) sugieren un método alternativo conocido como MCD (Minimum Covariance Determinant).
En general la distancia robusta Mahalanobis (RMD) viene dada por la siguiente expresión:
\[\begin{equation} RMD(\mathbf{x_i}) = \sqrt{(\mathbf{x_i} - \bar{\mathbf{X}}_{R})^T {\Sigma_R}^{-1} (\mathbf{x_i} - \bar{\mathbf{X}}_R)} \tag{4.4} \end{equation}\]
donde \(\bar{\mathbf{X}}_{R})\) y \({\Sigma_R}\) son los estimadores robustos para media y matriz de covarianza. Por ejemplo, se podría emplear el estimador robusto MVE o el MCD u otro. De igual manera a lo realizado anteriormente, la \(RMD(\mathbf{x_i})\) se comparará con el umbral que provee la distribución \(\chi^2\) con \(d\) grados de libertad.
Leys et al. (2018) sostienen que la distancia de Mahalanobis no es una buena aproximación para identificar valores atípicos, ya que utiliza las medias y las covarianzas de todos los datos (incluidos los outliers) para determinar las distancias individuales. P. Rousseeuw (1984) sugiere calcular la matriz robusta de covarianza mediante el uso del Determinante Mínimo de Covarianza (MCD por la sigla del término en inglés Minimum Covariance Determinant). La idea detrás de MCD es encontrar observaciones cuya covarianza tenga el menor determinante, produciendo un subconjunto de observaciones a partir del cual calcular las estimaciones de la media y covarianza.
El MCD calcula la media y la matriz de varianzas y covarianza empleando el subconjunto más central de datos (típicamente dos tercios de los datos), antes de calcular la distancia de Mahalanobis. Se considera que este es un método más sólido para identificar y eliminar valores atípicos que la distancia de Mahalanobis original.
El MCD implica los siguientes pasos:
- Buscar aquellas \(h\) observaciones cuya matriz de covarianza tiene el determinante más bajo posible.
- Calcular la media de estas \(h\) observaciones.
- Calcular la matriz de varianzas y covarianza de muestra de estas \(h\) observaciones (multiplicada por el factor de consistencia).
- Calcular la distancia de Mahalanobis con estos nuevos estimadores de la media y la matriz de varianzas y covarianzas y la expresión (4.4).
El cálculo de MCD es computacionalmente demandante, pero existen algunos algoritmos que pueden agilizar el cálculo.
4.3 Implementación en R
Para realizar un ejemplo práctico seguiremos usando los mismos datos que empleamos en los Capítulos 2 y 3. Los datos provienen de Hofmann (1994) y se encuentran en el archivo datos_credito.RData que se puede descargar de la página web del libro (https://www.icesi.edu.co/editorial/deteccion-anomalías). La descripción de las variables se encuentra en la Sección 2.4.
Carguemos los datos:
Los datos están cargados en el objeto de clase data.frame que denominamos german. Ese objeto tiene 14 variables y 1000 clientes. Seleccionemos solo las variables cuantitativas para poder aplicar las técnicas estudiadas en las secciones anteriores. Empleemos la función select_if() del paquete dplyr (Wickham et al., 2021) para hacer esta tarea más sencilla.
Noten que contamos con una matriz \(\textbf{X}_{n \times d}\) de dimensiones \(1000 \times 6\) (mil observaciones y 6 variables).
4.3.1 Distancia de Mahalanobis
La distancia de Mahalanobis se puede implementar en R por medio de la función mahalanobis() del paquete stats (R Core Team, 2013). Esta función calcula las distancias entre cada observación y el punto central de los datos empleando tres argumentos: x, center y cov. Similar a lo ya estudiado, el argumento x corresponde a los datos multivariados (de clase matrix o data.frame), center es el vector de medias de las variables y cov es la matriz de varianzas y covarianza de los datos.
La distancia de Mahalanobis para cada una de las observaciones teniendo en cuenta todas las variables cuantitativas se puede calcular con la siguiente línea de código:
# Encontrar las distancias de Mahalanobis para cada observación
MD <- mahalanobis(x = german_cuanti, center = colMeans(german_cuanti), cov = cov(german_cuanti))En la anterior línea de código hemos empleado las funciones colMeans() y cov() de la base de R para calcular el vector de medias (\(\bar{\mathbf{X}}\)) y la matriz de varianzas y covarianzas (\(\Sigma\)) de los datos, respectivamente.
Para determinar qué observaciones se pueden considerar outliers, comparemos la (\(MD(\mathbf{x_i})\)) con \(\chi^2_{6,0.025}\), tal como lo sugieren Cabana et al. (2021). El umbral lo podemos construir empleando la función qchisq() de la base de R. El código que genera el umbral será:
# Valor de corte
# p = 0.95 df = 6 con ncol(german_cuanti)
umbral <- qchisq(p = 0.975 , df = ncol(german_cuanti))Finalmente, para determinar que observaciones son outliers, podemos emplear el siguiente código:
## Obtener las observaciones superiores al valor de corte
anomalias_MD <- german_cuanti[MD > umbral,]Con este método hemos detectado 41 outliers. Una forma de visualizar estas observaciones es emplear un gráfico como el que se presenta en la Figura 4.1.
Figura 4.1: Clientes clasificados como outliers según la distancia de Mahalanobis
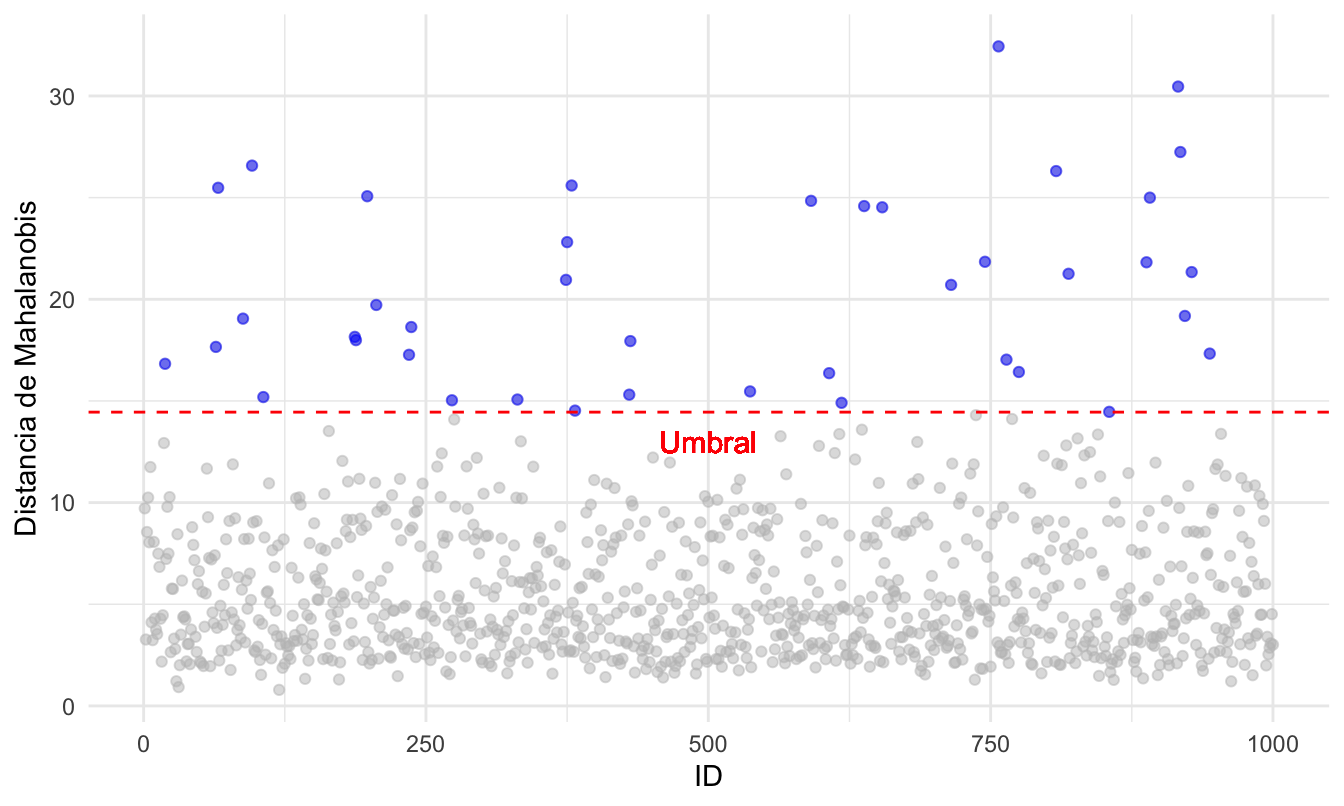
La Figura 4.1 fue creada empleando el paquete ggplot2 y la función gghighlight() del paquete gghighlight (Yutani, 2022). El código empleado fue el siguiente:
# Crear datos para la visaulización
MD_datos <- data.frame(ID = 1:1000, MD = MD)
library(ggplot2)
library(gghighlight)
# Construir la viualización
MD_datos %>%
ggplot(aes(x = ID, y = MD)) +
geom_point(color = "blue" , alpha= 0.5) +
ylab("Distancia de Mahalanobis") +
theme_minimal() +
gghighlight(MD > umbral, use_direct_label = F) +
geom_hline(yintercept=umbral, linetype="dashed", color = "red") +
geom_text( x=500, y=13,
label="Umbral",
size=4, color = "red") 4.3.2 Distancia robusta de Mahalanobis
La distancia robusta de Mahalanobis se puede obtener en R recurriendo a la función robustMD() del paquete faoutlier (Chalmers & Flora, 2015). Recuerden que esta función solo es posible aplicarla a variables continuas.
Los argumentos de esta función son los datos multivariados que pueden ser de clase matrix o data.frame (x) y el método robusto de estimación de los parámetros de la media (\(\bar{\mathbf{X}}\)) y la matriz de varianzas y covarianzas (\(\Sigma\)) (method). Si empleamos method = “mve”, se estimarán estos parámetros con el método elipsoide de volumen mínimo (MVE) sugerido por P. Rousseeuw & Zomeren (1990). Si method = “mcd” se empleará el método MCD sugerido por autores como EStimator (1999) y P. Rousseeuw (1984).
Ahora calculemos primero la distancia robusta de Mahalanobis empleando el método MVE. En este caso el código será:
#install.packages("faoutlier")
library(faoutlier)
RMD_MVE <- robustMD(german_cuanti, method ="mve" )Si corres este código, obtendrás un mensaje de error44. El error ocurre porque la variable dependientes solo toma dos valores (1 y 2) y por tanto el IQR es cero. Esto no permite el cálculo de la matriz de varianzas y covarianzas con el método MVE. Por eso, para emplear este método retiraremos esta variable (la sexta columna) que no genera variabilidad. En este caso el código será:
#install.packages("faoutlier")
library(faoutlier)
RMD_MVE <- robustMD(german_cuanti[,1:5], method ="mve" )
RMD_MVE## mah p sig
## 916 146.15509 0 ****
## 96 116.24271 0 ****
## 638 107.19605 0 ****
## 819 105.74878 0 ****
## 888 102.73827 0 ****
## 918 102.23408 0 ****
## 375 100.93038 0 ****
## 379 98.65572 0 ****
## 745 92.45154 0 ****
## 715 87.81617 0 ****La salida de esta función no solo muestra la distancia robusta de Mahalanobis sino que también la compara con el respectivo umbral y presenta el respectivo valor p. Pero tienes que tener cuidado, pues por defecto solo presenta las primeras 10 observaciones con la mayor distancia. Esto no significa que estas sean las únicas observaciones consideradas outliers. En el slot $mahdel objeto RMD_MVE podemos encontrar la distancia robusta de Mahalanobis. De manera similar a lo que hicimos anteriormente, podemos ver cuáles son los outliers con el siguiente código:
# Valor de corte
# p = 0.95 df = 5 con ncol(german_cuanti)-1
umbral <- qchisq(p = 0.975 , df = ncol(german_cuanti)-1)
## Obtener las observaciones superiores al valor de corte
anomalias_RMD_MVE <- german_cuanti[RMD_MVE$mah > umbral,]En este caso obtenemos 187 outliers. Una forma alternativa para obtener los outliers es empleando el valor p con el siguiente código:
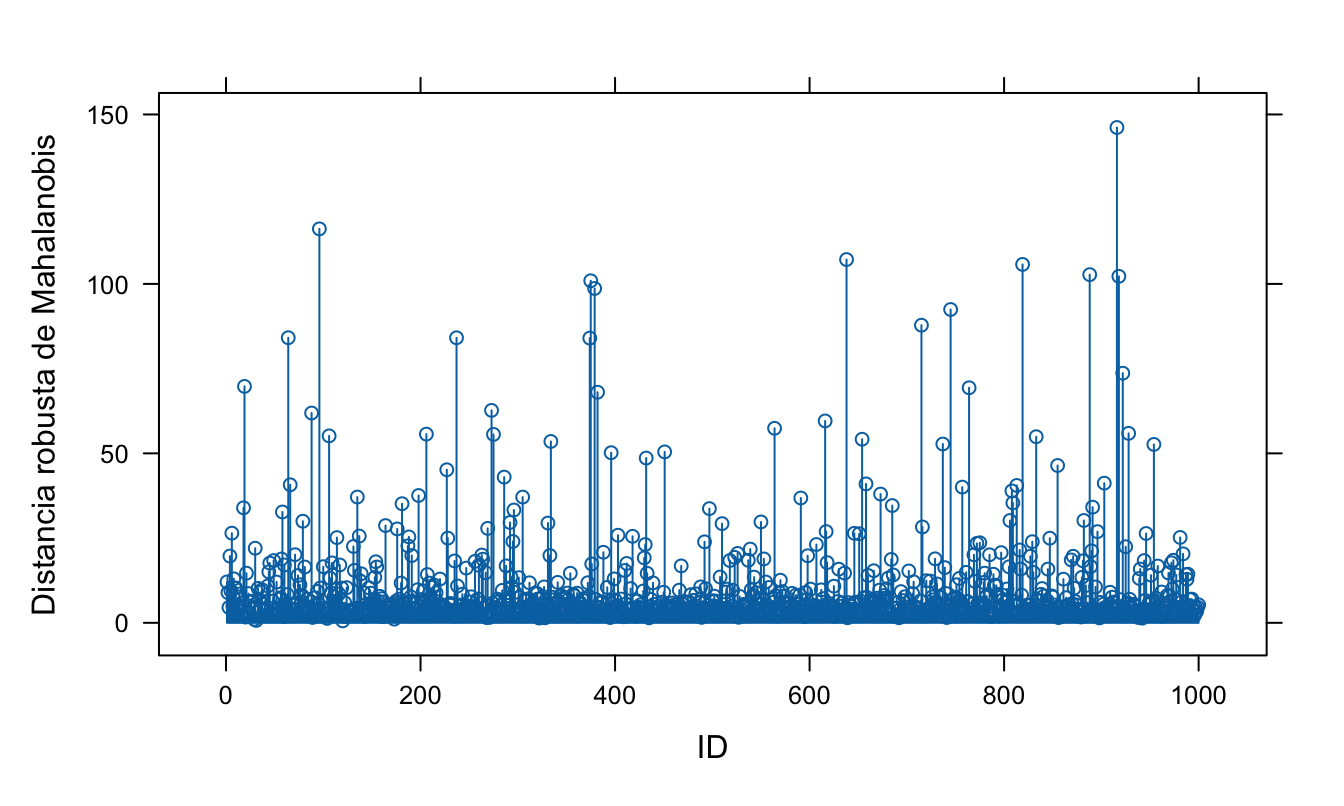
Por otro lado, el paquete faoutlier permite construir rápidamente una visualización similar a la Figura 4.1, pero la gráfica se generará con la base de R y no con el paquete ggplot2. El código que genera la Figura 4.2 es el siguiente:
Figura 4.2: Clientes atípicos según la distancia robusta de Mahalanobis calculada con el método MVE
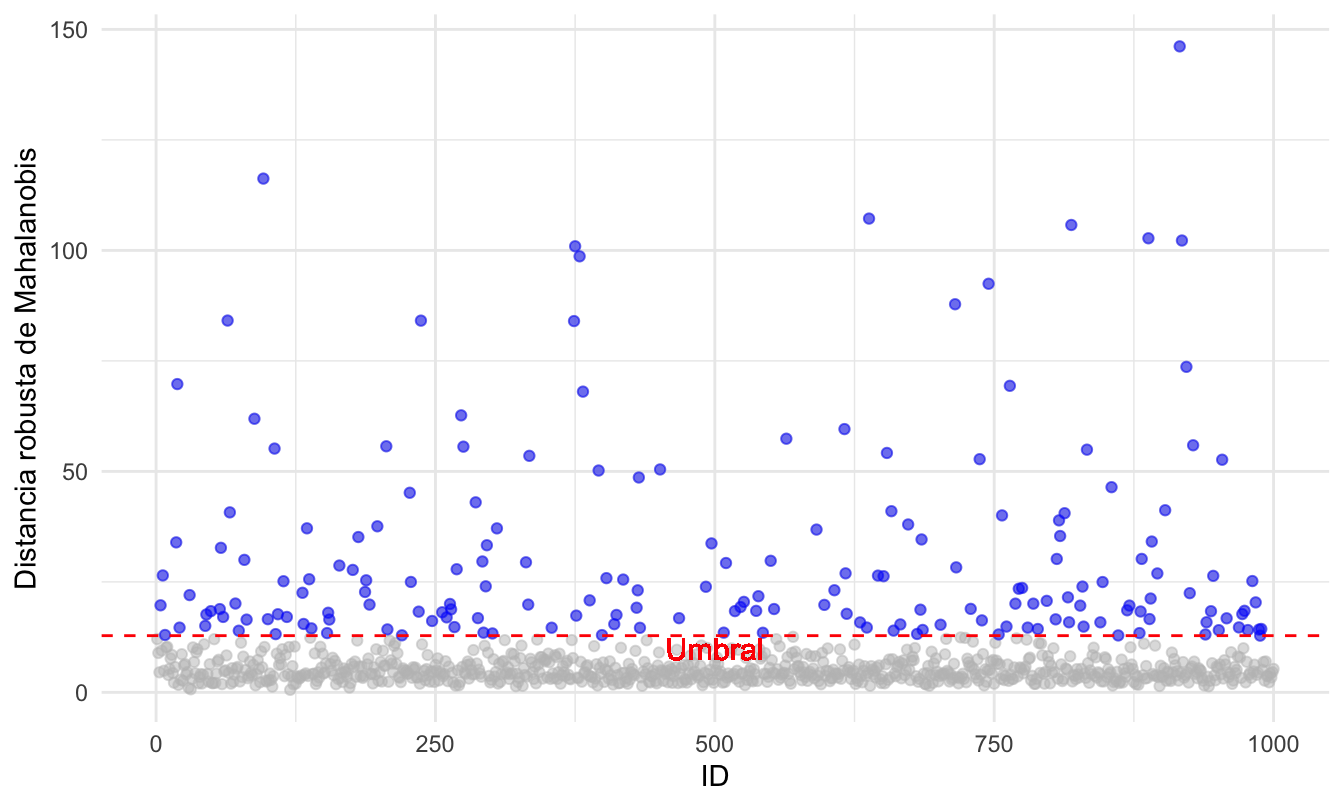
Podemos mejorar la Figura 4.2 empleando el paquete ggplot, obteniendo una visualización como la que se presenta en la Figura 4.3. Intencionalmente no presentamos el código que genera dicha figura, ¡intenta reproducirla!
Figura 4.3: Clientes atípicos según la distancia robusta de Mahalanobis calculada con el método MVE empleando ggplot2
Ahora calculemos la distancia robusta de Mahalanobis empleando el método MCD. El código sería:
Si corres este código, nuevamente obtendrás el mismo mensaje de error que antes45 Eliminando la variable dependientes la función tampoco podrá calcular esta distancia. Ahora la razón es diferente46, no se puede encontrar la inversa de la matriz de varianzas y covarianzas porque existen unas columnas que están muy correlacionadas (no son linealmente independientes). Si inspeccionamos con más cuidado los datos, las variables porcentaje.disponible, residente y numero.creditos solo toman cuatro valores (1, 2, 3 y 4) y por tanto funcionan más como variables cualitativas que cuantitativas, no presentan mucha dispersión. Por eso el cálculo de la matriz de varianzas y covarianzas con el método MCD no es posible. Por eso, para emplear este método retiraremos estas variables, dejando solo monto.credito y edad (la primera y cuarta columnas). En este caso el código será:
En este caso, los outliers los obtenemos (de manera análoga al caso anterior) de la siguiente manera:
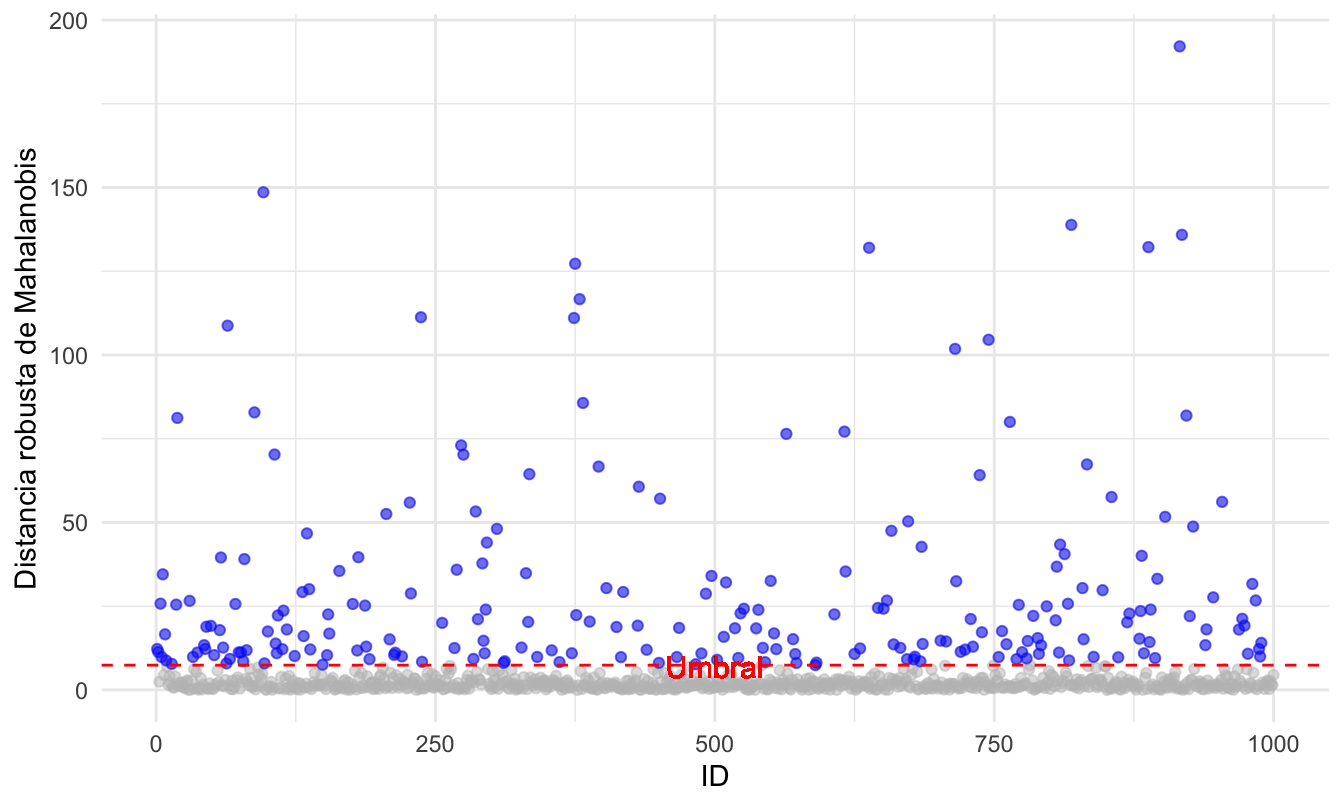
Ahora tenemos 222 outliers. Y en la Figura 4.4 se visualizan estas distancias. Intencionalmente no presentamos el código que genera dicha figura, ¡intenta reproducirla!
Figura 4.4: Clientes atípicos según la distancia robusta de Mahalanobis calculada con el método MCD empleando ggplot2
4.4 El caso de dos features
Cuando se cuenta con solo dos variables, es común que se emplee una aproximación gráfica para identificar los outliers multivariados con la distancia de Mahalanobis. La visualización implica tener en los ejes cada una de las variables y dibujar elípses para representar niveles de igual distancia de Mahalanobis. Cada elipse corresponde a un valor constante de distancia de Mahalanobis y el centro de las elípses corresponde a las medias de las variables. También es común no pintar todas las elípses, sino solo la que corresponde al umbral a partir del cual la distancia de Mahalanobis se considera muy grande y por tanto las observaciones por fuera de la elipse son etiquetadas como outliers.
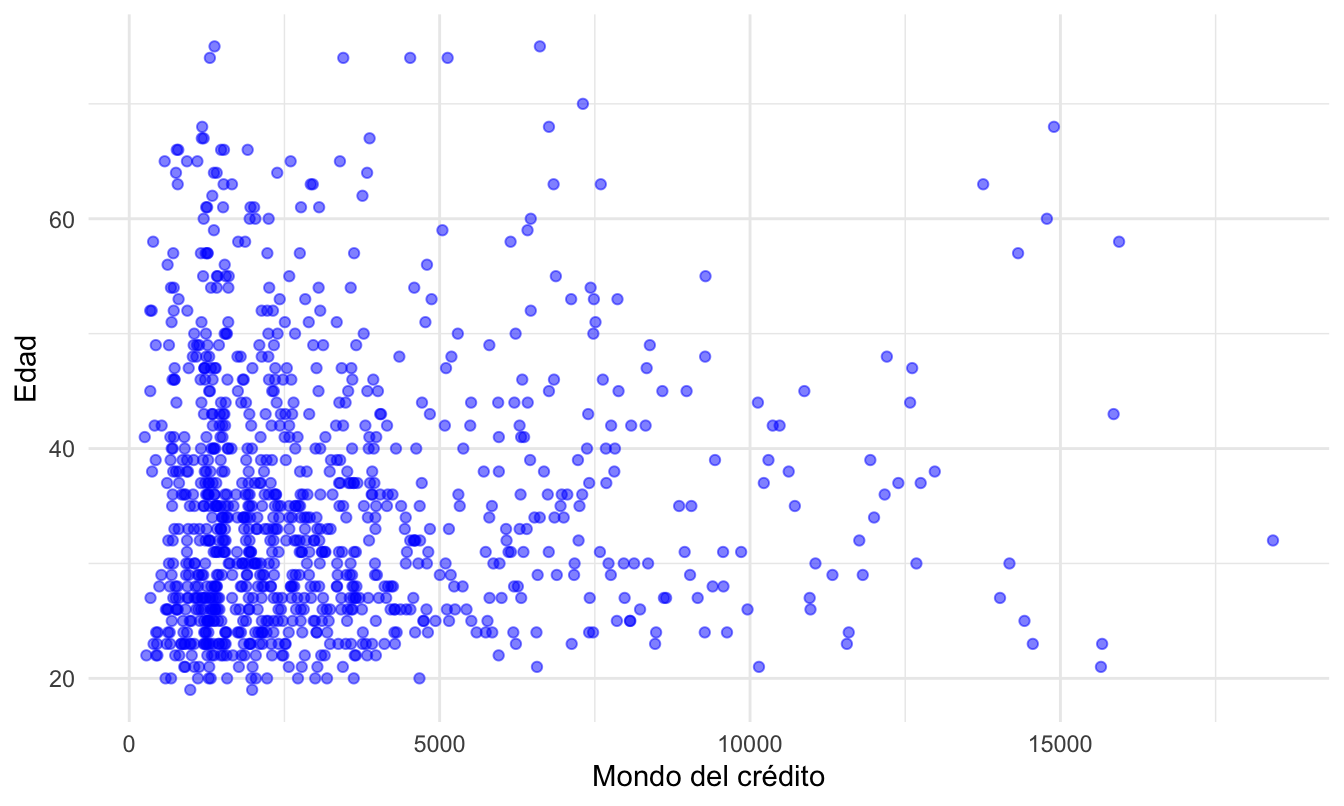
Por ejemplo, consideremos solo las variables monto.credito y edad. El correspondiente diagrama de dispersión se presenta en la Figura 4.5. Intencionalmente no presentamos el código que genera dicha figura.
Figura 4.5: Edad y monto de crédito para los clientes del banco
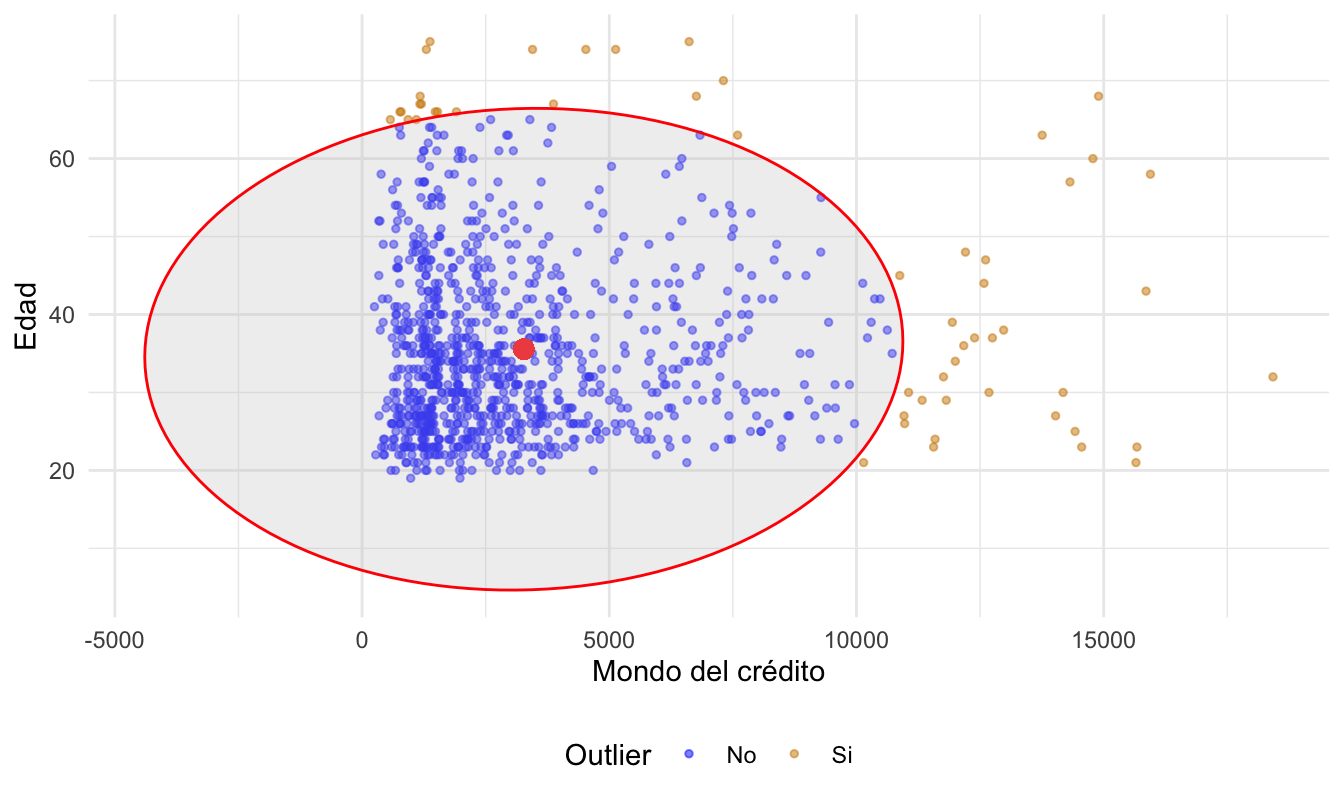
Ahora podemos incluir una elipse con el umbral para la distancia de Mahalanobis para visualizar los outliers como en la Figura 4.6. El código se ha omitido intencionalmente.
Figura 4.6: Edad y monto de crédito para los clientes del banco con umbral de la distancia de Mahalanobis.
Este tipo de visualizaciones como la Figura 4.6 es muy común cuando solo se cuenta con dos variables, pero en el business analytics es muy rara la situación en la que solo contemos con dos features. Si deseas obtener una visualización como la Figura 4.6 sin tener que construirla manualmente (como fue nuestro caso), podemos emplear la función drawMahal() que viene en el paquete chemometrics (Filzmoser, 2023).
La función drawMahal() emplea cuatro argumentos principalmente:
donde:
- x: los datos multivariados que pueden ser de clase matrix o data.frame.
- center: El centro de los datos; es decir, los valores medios de las variables.
- covariance: La matriz de varianzas y covarianzas de los datos.
- quantile. Los cuantiles de distancia a graficar. Recuerda que Cabana et al. (2021) sugieren emplear \(\alpha\) en 0,025; es decir, emplear el umbral en el 2,5% de observaciones más extremas. que equivale a emplear el cuantil 0.975 (probabilidad de 97.5%) Es decir, cualquier observación fuera de 97.5% de probabilidad se considerará un valor atípico.
En este caso, el código para tener todos los elementos necesarios para crear la Figura 4.7 es:
# install.packages("chemometrics")
library(chemometrics)
# Seleccionar las variables a analizar
datos_mah <- german_cuanti[c("monto.credito" , "edad")]
# Encontrar el punto central
datos_mah.center = colMeans(datos_mah)
# Encontrar la matriz de covarianzas
datos_mah.cov = cov(datos_mah)Ahora sí podemos emplear la función drawMahal() para obtener la Figura 4.7. El código correspondiente es:
Figura 4.7: Edad y monto de crédito para los clientes del banco con umbral de la distancia de Mahalanobis creada automáticamente.
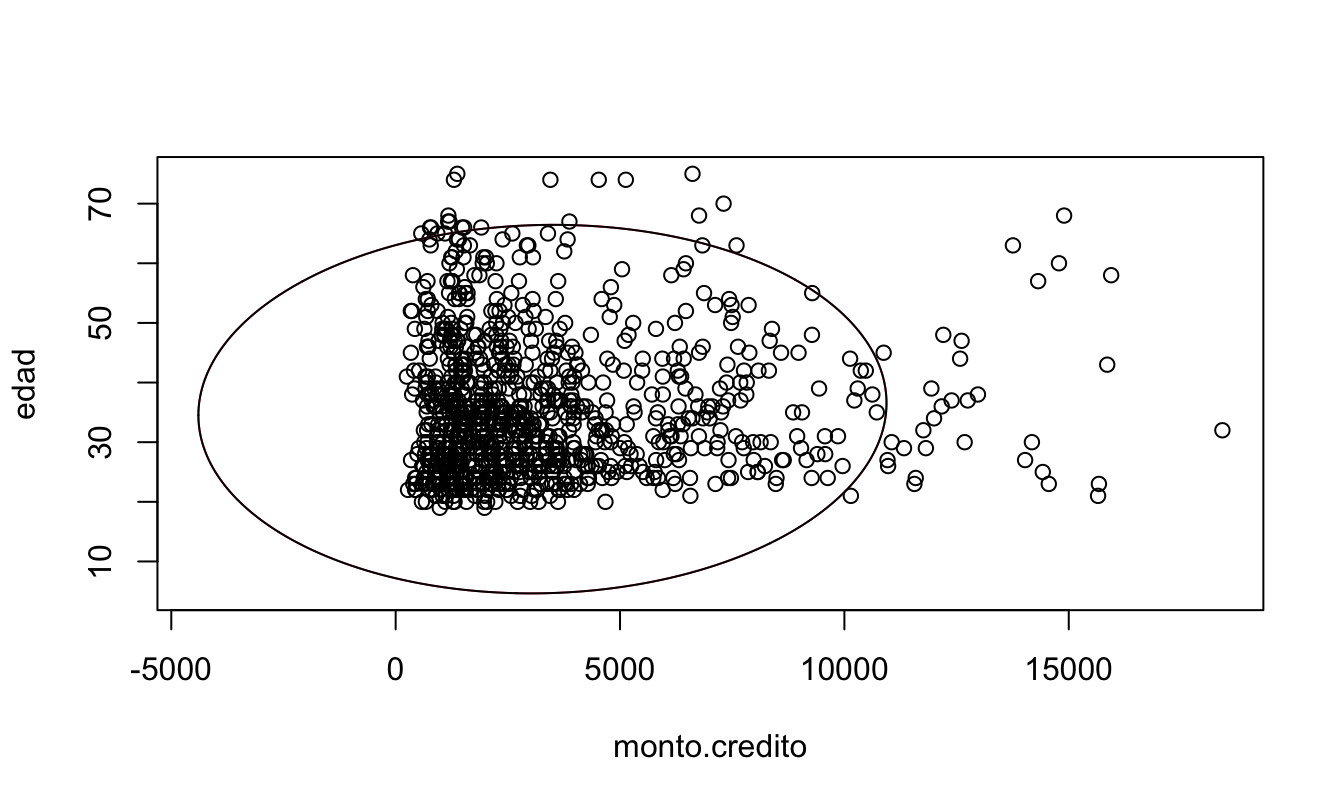
Nota que en este caso no hemos calculado la distancia de Mahalanobis con estimadores robustos. Podríamos emplear la función covMcd() del paquete robustbase (Maechler et al., 2024). para estimar la media y la varianza robustas empleando el método MCD y reemplazar estos valores en los argumentos center y covariance de la función drawMahal(). Para calcular la matriz de varianzas y covarianzas robusta por el método EVM, podemos emplear la función cov.rob() del paquete MASS (Venables & Ripley, 2002), con el argumento method = “mve”. ¡Inténtalo!
4.5 Comentarios finales
En este capítulo estudiamos cómo emplear la distancia de Mahalanobis para detectar anomalías multivariadas. La distancia de Mahalanobis y sus variantes robustas permiten identificar outliers multivariados. Su principal fortaleza es capturar relaciones entre variables, pero su aplicación depende de que los datos tengan una estructura aproximadamente elíptica. Por ello, conviene usarlas en conjunto con técnicas exploratorias vistas en capítulos previos. Estas técnicas, al igual que las estudiadas en los Capítulos 2 y 3, permiten encontrar anomalías que se pueden caracterizar como anomalías globales (puntuales); es decir, outliers.
Es importante recalcar que tanto las aproximaciones multivariadas como las univariadas no son mutuamente excluyentes. En el proceso de ETL es muy común el uso de técnicas univariadas para la detección de outliers, por otro lado, es en el proceso de EDA en el que el análisis de outliers multivariados como los estudiados en este capítulo y en 5 es más común. Las herramientas estudiadas hasta aquí se deben entender como complementarias y parte de la caja de herramientas que todo científico de datos debe tener a la mano, independientemente del tipo de preguntas de negocio que estemos intentando responder.
En este capítulo ampliamos la caja de herramientas para la detección de valores atípicos. En los Capítulos 5 y 6 emplearemos más herramientas con un origen en la estadística. Para posteriormente adentrarnos en las técnicas de detección de anomalías con un origen en el aprendizaje de máquina.
Referencias
Recuerda, que como lo hemos discutido en los capítulos anteriores, no toda anomalía es un outlier pero todo outlier es una anomalía.↩︎
En la Sección 2.2 de Alonso et al. (2025) se presenta una discusión de las diferentes distancias y cómo se emplean estas en los algoritmos de clústering.↩︎
En el Capítulo 6 de Alonso & Hoyos (2025) se presenta una discusión de como se emplean las diferentes distancias en el algoritmo kNN.↩︎
En la Sección 2.2 de Alonso et al. (2025) puedes consultar una presentación más detallada de estas distancias.↩︎
Por eso esta distancia también es conocida como la distancia estadística o distancia ponderada.↩︎
El mensaje de error será algo como “Error in cov.rob(data, method = method, …) : at least one column has IQR 0”.↩︎
El mensaje de error será algo como “Error in cov.rob(data, method = method, …) : at least one column has IQR 0”.↩︎
El mensaje de error es “Error in solve.default(cov, …): Lapack routine dgesv: system is exactly singular: U[5,5] = 0”.↩︎