5 Empleando PCA para detectar anomalías

5.1 Introducción

En los Capítulos 2 y 3 estudiamos métodos de origen en la estadística para detectar outliers (anomalías univariadas puntuales). Adicionalmente, en el Capítulo 4 discutimos cómo encontrar outliers multivariados . En este capítulo estudiaremos una técnica para detectar anomalías multivariadas empleando el análisis de Componentes Principales (PCA por las siglas del término en inglés Principal Component Analysis)47 El PCA es una técnica matemática que permite resumir la información contenida en muchas variables en unas pocas. Si bien esta técnica es de origen en las matemáticas, la estadística la ha adoptado como propia y hoy hace parte de las herramientas convencionales de todo usuario de la estadística que emplea muchas variables (muchas dimensiones en la jerga del PCA). A este procedimiento se le conoce técnicamente como reducción de la dimensionalidad de los datos.

El PCA es un procedimiento matemático que no requiere supuestos, ni siquiera sobre la distribución probabilística de los datos, que busca reducir las dimensiones. En este capítulo primero estudiaremos la intuición detrás del procedimiento (Sección 5.2), para después concentrarnos en el detalle técnico del PCA (Sección 5.3)) para posteriormente mostrar en la Sección 5.4 cómo se emplea esta técnica para encontrar outliers. Posteriormente, estudiaremos cómo aplicar este procedimiento en R (Sección 5.5.1).

5.2 La intuición detrás del PCA

Por un momento, imaginémonos que contamos con una base de datos (data.frame) que tiene \(d\) variables y para cada variable tenemos \(n\) observaciones.

\[\begin{equation} \begin{matrix} x_{1,1} & x_{2,1} & \cdots & x_{d,1}\\ x_{1,2} & x_{2,2} & \cdots & x_{d,2}\\ \vdots & \vdots & \vdots & \vdots\\ x_{1,n} & x_{2,n} & \cdots & x_{d,n} \end{matrix} \tag{5.1} \end{equation}\]
En este caso, estamos empleando el primer subíndice para denotar el número de la variable y el segundo el número de la observación. Esta notación sigue el estándar de la estadística para denotar matrices de datos, donde las columnas son las variables y las filas son las observaciones. Esta es la misma notación que se emplea típicamente en el contexto de la regresión múltiple (Alonso, 2024). En otras palabras, \(x_{j,i}\) representa la observación \(i\)-ésima de la variable \(j\), donde \(j=1, 2, \cdots d\) (tenemos \(d\) variables) y \(i=1, 2, \cdots n\) (tenemos \(n\) observaciones). No sigue el estándar del álgebra matricial donde el primer subíndice corresponde a la fila y el segundo a la columna.

Nota que al calcular estadísticas descriptivas lo que hacemos es concentrarnos en una columna de la base de datos y resumirla con un número. Las entradas de la base de datos corresponden a observaciones que se emplean para estimar (encontrar) el estadístico descriptivo (como la media48) que no es observable.

El PCA es algo diferente, a partir de varias columnas (variables) observadas se quiere encontrar otras variables no observables que las resuman. Esas variables no observables se conocen como componentes principales. La Figura 5.1 presenta un diagrama de esta idea.



Figura 5.1: Representación del PCA

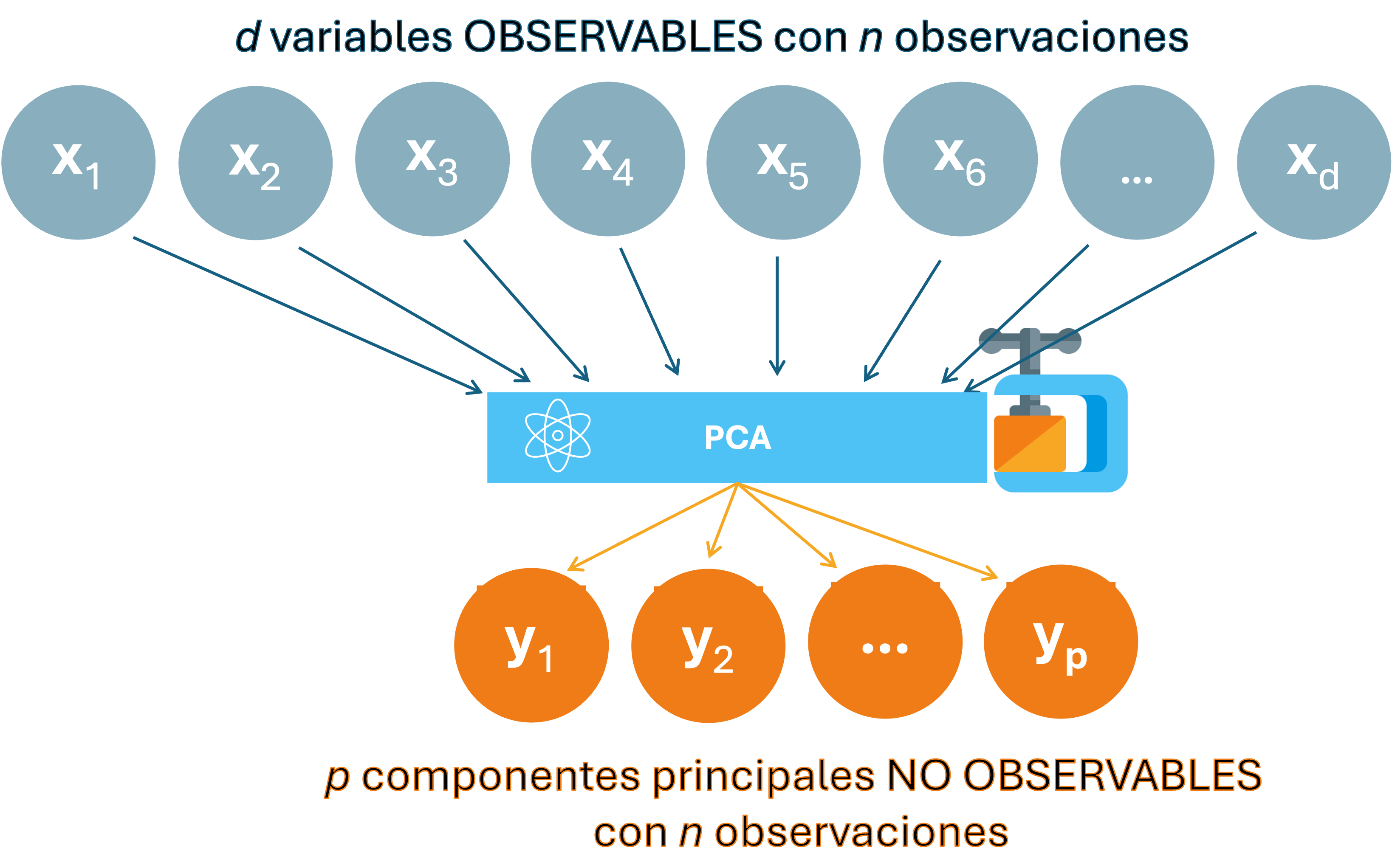
Representación del PCA
Fuente: adaptación de Alonso (2020).




Figura 5.2: Material multimedia: PCA

Material multimedia: PCA
Fuente: elaboración propia. https://ln.run/MHDAW


En otras palabras, tras el PCA no tendremos las \(d\) variables originales, sino que tendremos \(p\) componentes principales que resumen las \(d\) variables originales. Es decir, ahora tendremos:

\[\begin{equation} \begin{matrix} y_{1,1} & y_{2,1} & \cdots & y_{p,1}\\ y_{1,2} & y_{2,2} & \cdots & y_{p,2}\\ \vdots & \vdots & \vdots & \vdots\\ y_{1,n} & y_{2,n} & \cdots & y_{p,n} \end{matrix} \tag{5.2} \end{equation}\]

Para que el ejercicio de PCA tenga sentido, se espera que \(p\) sea sustancialmente menor que \(d\).

5.3 Detalle técnico del PCA

Formalmente, queremos partir de una matriz de datos con las \(d\) variables observadas que se desean resumir. Es decir,

\[\begin{equation} \textbf{X}_{n \times d}=\begin{bmatrix} x_{1,1} & x_{2,1} & \cdots & x_{d,1}\\ x_{1,2} & x_{2,2} & \cdots & x_{d,2}\\ \vdots & \vdots & \vdots &\vdots \\ x_{1,n} & x_{2,n} & \cdots & x_{d,n} \end{bmatrix} \tag{5.3} \end{equation}\]

Y la tarea será encontrar \(p\) componentes principales. En otras palabras debemos encontrar \[\begin{equation} \textbf{Y}_{n \times p}=\begin{bmatrix} y_{1,1} & y_{2,1} & \cdots & y_{p,1}\\ y_{1,2} & y_{2,2} & \cdots & y_{p,2}\\ \vdots & \vdots & \vdots & \vdots\\ y_{1,n} & y_{2,n} & \cdots & y_{p,n} \end{bmatrix} \tag{5.4} \end{equation}\]

Esto implica encontrar una matriz \(\mathit{\textbf{W}}_{d \times p}\) que cumpla la siguiente condición: \[\begin{equation} \textbf{Y}_{n \times p}= \textbf{X}_{n \times d}\mathit{\textbf{W}}_{d \times p} \tag{5.5} \end{equation}\]

La matriz \(\mathit{\textbf{W}}_{d \times p}\) es conocida como la matriz de cargas (loadings). Donde, \[\begin{equation} \mathit{\textbf{W}}_{d \times p}=\begin{bmatrix} \gamma_{1,1} & \gamma_{2,1} & \cdots & \gamma_{p,1}\\ \gamma_{1,2} & \gamma_{2,2} & \cdots & \gamma_{p,2}\\ \vdots & \vdots & \vdots & \vdots\\ \gamma_{1,d} & \gamma_{2,d} & \cdots & \gamma_{p,d} \end{bmatrix} \tag{5.6} \end{equation}\]

De esta manera, cada uno de los \(p\) componentes principales para la \(i\)-ésima observación será: \[\begin{equation} \begin{matrix} y_{1,i} = \gamma_{1,1}x_{1,i} + \gamma_{1,2}x_{2,i} + \gamma_{1,3}x_{3,i} + \vdots + \gamma_{1,p}x_{d,i} \\ y_{2,i} = \gamma_{2,1}x_{1,i} + \gamma_{2,2}x_{2,i} + \gamma_{2,3}x_{3,i} + \vdots + \gamma_{2,p}x_{d,i}\\ \vdots \\ y_{p,i} = \gamma_{p,1}x_{1,i} + \gamma_{p,2}x_{2,i} + \gamma_{p,3}x_{3,i} + \vdots + \gamma_{p,d}x_{d,i} \end{matrix} \end{equation}\]

Las cargas \(\gamma_{j,l}\) se interpretan como el aporte de la variable \(l\) al componente principal \(j\). Nota que los \(p\) componentes principales son una combinación lineal de las variables y los \(\gamma\)s son las ponderaciones de cada variable en el respectivo componente principal.

Ahora, la pregunta será cómo encontramos la matriz \(\mathit{\textbf{W}}_{d \times p}\). La respuesta es relativamente sencilla si se emplean resultados del álgebra matricial. Para encontrar los componentes principales se debería buscar aquellos que puedan explicar la mayor cantidad de la varianza de las variables originales. Y dado que en este caso se trata de más de una variable, pues en últimas lo que queremos es poder explicar la mayor parte de la matriz de varianzas y covarianzas de los datos originales (\(\Sigma_{d \times d}\)), esta aproximación se conoce como la maximización de la varianza. Por otro lado, es muy fácil demostrar que maximizar la varianza explicada es equivalente a encontrar los factores propios que impliquen la menor distancia promedio elevada al cuadrado (media cuadrática) entre los componentes principales y los vectores (variables) originales. A este método se le conoce como minimizar el error cuadrado. En cualquiera de los dos casos, para \(p\) factores propios se tiene que la matriz \(\mathit{\textbf{W}}_{d \times p}\) implica encontrar los \(p\) vectores y valores propios de la matriz de varianzas y covarianzas de los datos originales (\(\Sigma_{d \times d}\)). Esto permitirá encontrar \(p\) factores propios que serán ortogonales entre sí. Es decir, cada una de las nuevas variables creadas será independiente entre sí.

Antes de continuar, es importante mencionar que no es común que todas las variables originales se midan en las mismas unidades. Por eso, una buena práctica es estandarizar las variables para dar la misma influencia a cada una de ellas.

Para encontrar los \(p\) valores propios que resuman las \(d\) variables originales se tendrán que seguir los siguientes pasos:

  1. Estandarizar los datos originales. Por simplicidad, llamemos a estos datos \(\textbf{X}_{n \times d}\).
  2. Calcular la matriz de varianzas y covarianzas de los datos originales. En otras palabras, a partir de \(\textbf{X}_{n \times d}\), encontrar la matriz de varianzas y covarianzas \(\Sigma_{d \times d}\).
  3. Calcular todos los vectores propios y sus valores correspondientes.
  4. Ordenar los vectores propios de acuerdo con sus valores propios en orden decreciente.
  5. Elegir los primeros \(p\) vectores propios y esas serán las nuevas \(p\) dimensiones.
  6. Transformar las \(n\) observaciones de \(\textbf{X}_{n \times d}\) en los nuevos \(p\) componentes principales \(\textbf{Y}_{n \times p}\).

El PCA solo se puede realizar con variables cuantitativas. Una de las tareas importantes al realizar un PCA es determinar el número de componentes principales (\(p\)) (paso 5). Para esto típicamente se emplean uno de los siguientes tres criterios (Ver Alonso (2020) para una mayor discusión) para determinar el “mejor” número de componentes (en inglés se conocen como stopping rules):

  • criterio del codo (o también conocido como scree test),
  • la regla de Keisser-Guttman y
  • el análisis paralelo (también conocido como análisis paralelo de Horn).

El criterio del codo implica crear un gráfico de codo (elbow graph, también conocido como “scree plot”) que muestra la proporción de la varianza de todos los datos explicada por cada uno de los componentes principales. Esto se hace graficando en el eje horizontal el número de componentes principales y en el vertical la división de la varianza de cada componente principal entre la varianza total de todos los componentes principales.

El gráfico de codo muestra cómo disminuye la varianza explicada a medida que aumenta el número de componentes. En ese gráfico debemos identificar el “codo”, entendido como el punto donde la disminución de la varianza explicada se hace menos pronunciada; es decir, donde la curva comienza a aplanarse. Este punto sugiere que añadir más componentes principales no proporciona una mejora significativa en la explicación de la variabilidad de los datos.

De esta manera, el número de componentes principales donde se presenta el “codo” será considerado como el número óptimo de componentes (\(p\)).

El método del codo es considerado como una técnica heurística y “subjetiva” pues depende de la experiencia del científico de datos para detectar el “codo”. Es más, en algunos casos puede no haber un “codo” evidente.

Por otro lado, la regla de Keisser-Guttman implica mantener aquellos componentes cuyos valores propios son superiores a uno. La idea detrás de esto es que los valores propios representan la proporción de la varianza total descrita por cada componente. Así, al mantener solo aquellos mayores a uno, estamos reteniendo los componentes que explican más de la variabilidad que las variables originales.

Otra forma de determinar el número óptimo de componentes principales fue sugerida por Horn (1965). El análisis paralelo, también conocido como análisis paralelo de Horn, es un método estadístico que nos permite determinar \(p\). El método compara los valores propios generados a partir de los datos originales con los valores propios generados a partir de una matriz simulada (se realizan simulaciones de Monte-Carlo) creada a partir de datos aleatorios del mismo tamaño (para mayor detalle consultar a Horn (1965)). Al igual que el criterio anterior se retienen aquellos componentes con valores propios simulados (ajustados) mayores a uno.

5.4 PCA para detectar anomalías

Hasta el momento hemos estudiado cómo realizar un PCA, pero no hemos discutido cómo emplear el PCA para detectar anomalías en una muestra. Una vez tenemos las \(n\) observaciones de las \(d\) variables ( \(\textbf{X}_{n \times d}\)) transformadas en los nuevos \(p\) componentes principales (\(\textbf{Y}_{n \times p}\)), una de las prácticas más comunes es visualizar los valores de los componentes principales (típicamente los dos primeros componentes principales) con un gráfico de dispersión, teniendo en el eje horizontal el primer componente y en el vertical el segundo componente. Los puntos que están muy alejados de la mayoría de los puntos pueden considerarse outliers. Otra aproximación gráfica es visualizar con boxplots los valores de cada uno de los componentes principales para cada observación.

Otros autores sugieren no graficar directamente los componentes principales, sino la distancia Mahalanobis. Es decir, después de realizar el PCA, se calcula la distancia Mahalanobis de cada observación al centroide (o centro) de los datos en el espacio de las componentes principales (En la Sección 4.3.1 discutimos esta distancia en detalle). Las observaciones que tienen una distancia Mahalanobis alta pueden considerarse outliers.

Como se discutió en la Sección 4.3.1, la distancia de Mahalanobis, se define como: \[\begin{equation} d(\mathbf{y_i}) = \sqrt{(\mathbf{y_i} - \bar{\mathbf{Y}})^T \Sigma^{-1} (\mathbf{y_i} - \bar{\mathbf{Y}})} \tag{5.7} \end{equation}\] en este caso, \(\mathbf{y_i}\) representa el vector de los valores que toman los componentes principales para la observación \(i\)-ésima; en otras palabras, la \(i\)-ésima fila de la matriz \(\textbf{Y}_{n \times p}\). Por otro lado, \(\bar{\mathbf{Y}}\) corresponde al vector que contiene las medias para cada componente principal; es decir, la media de cada columna de la matriz \(\textbf{Y}_{n \times p}\). Y finalmente, \[\begin{equation} \Sigma = \begin{bmatrix} S_1^2 & S_{1,2} & \cdots & S_{1,d} \\ S_{1,2} &S_2^2 & \cdots & S_{2,d} \\ \vdots & \vdots & \ddots & \vdots \\ S_{1,d} & S_{2,d} & \cdots &S_d^2 \\ \end{bmatrix} \tag{5.8} \end{equation}\] donde \(S_{k,l}\) es la covarianza entre el \(k\)-ésimo componente principal (columna \(k\) de la matriz \(\textbf{Y}_{n \times p}\)) y el \(l\)-ésima componente principal y \(S_k^2\) es la varianza del \(k\)-ésima componente principal.

Es importante recordar (como lo estudiamos en la Sección 4.3.1) que la distancia euclidiana solo toma en cuenta la magnitud de las diferencias entre las coordenadas de dos puntos, sin considerar la correlación entre las variables. En cambio, la distancia de Mahalanobis incorpora la información de la matriz de covarianza, ponderando las diferencias entre las variables de acuerdo con su importancia y correlación. Adicionalmente, se ha documentado que la distancia de Mahalanobis es menos sensible a la presencia de outliers o valores extremos en el conjunto de datos. Esto la convierte en una medida de distancia muy empleada en muestras multivariables (multidimensionales) donde las variables están interrelacionadas y existen outliers.

Otra forma de emplear el análisis de PCA para la detección de anomalías es construir un Score de Anomalía. Esta aproximación implica calcular una puntuación de anomalía para cada observación de la siguiente manera:

\[\begin{equation} Score_i = \sum_{j=1}^{p} \left( \frac{y_{j,i}^2}{\lambda_j} \right) \tag{5.9} \end{equation}\]

con \(\lambda_j\) representando el valor propio (eigenvalue) asociado con el \(j\)-ésimo componente principal. Recuerda que \(Y_{j,i}\) es el valor del \(j\)-ésimo componente principal para la observación \(i\) (originalmente \(x_i\)).

Las observaciones con scores más altos se consideran que tienen una probabilidad más alta de ser outliers. El uso de los scores de anomalía en lugar de medidas directas de distancia como la distancia Mahalanobis de los componentes principales puede ser útil porque tiene en cuenta la varianza explicada por cada componente principal, lo que puede ayudar a identificar outliers en conjuntos de datos multidimensionales de manera más efectiva. El problema que trae emplear estos scores de anomalía es que no existe un umbral claro para establecer que una observación es un outlier.

5.5 Implementación en R

Antes de realizar la detección de anomalías empleando el PCA, veamos en detalle cómo realizar un PCA en R. Si ya dominas esta técnica, puedes saltarte esta subsección. Si quieres estudiar en más detalle el PCA, puedes consultar Alonso (2020).

5.5.1 PCA en R

Para realizar un ejemplo práctico, seguiremos usando los mismos datos que empleamos en los Capítulos 2, 3 y 4. Los datos provienen de Hofmann (1994) y se encuentran en el archivo datos_credito.RData que se puede descargar de la página web del libro (https://www.icesi.edu.co/editorial/deteccion-anomalias). La descripción de las variables se encuentra en la Sección 2.4. Carguemos los datos:

load("./datos/datos_credito.RData")

Los datos están cargados en el objeto de clase data.frame que denominamos german. Ese objeto tiene 14 variables y 1000 clientes. Seleccionemos solo las variables cuantitativas para poder aplicar las técnicas estudiadas en las secciones anteriores. Empleemos la función select_if() del paquete dplyr (Wickham et al., 2021) para hacer esta tarea más sencilla. 

library(dplyr)
german_cuanti <- german %>% 
     select_if(is.numeric)

Es decir, en este caso contamos con una matriz \(\textbf{X}_{n \times d}\) de dimensiones \(1000 \times 6\) (mil observaciones y 6 variables).

En R es posible realizar el PCA con diferentes paquetes como psych (William Revelle, 2023), ade4 (Bougeard & Dray, 2018) , amap (Lucas, 2022) , ca (Nenadic & Greenacre, 2007) y MASS (Venables & Ripley, 2002) , aún con la función princomp() del core de R. Nosotros emplearemos el paquete FactoMineR (Lê et al., 2008) .

La función PCA() del paquete FactoMineR típicamente incluye los siguientes argumentos:

PCA(X, scale.unit, ncp, quanti.sup, quali.sup, graph, axes

donde:

  • X: La matriz de datos originales \(\textbf{X}_{n \times d}\) (sin estandarizarse).
  • scale.unit: Si scale.unit = TRUE (valor por defecto), los datos son estandarizados.
  • ncp: \(p\). Número de factores propios.
  • graph: Si graph = TRUE (opción por defecto), se presenta un gráfico (biplot) de dispersión para cada variable incluida en el análisis y con dos componentes principales en cada uno de los ejes.
  • axes: Un vector de tamaño dos que especifica qué componentes principales serán graficados.

Empleemos esta función para calcular inicialmente el PCA con \(p = 6\). Naturalmente, esto no ayuda a reducir las dimensiones, pero si nos permitirá escoger en un paso posterior el mejor \(p\).

library(FactoMineR)
pca_inicial <- PCA(german_cuanti, graph = FALSE)
summary(pca_inicial)
## 
## Call:
## PCA(X = german_cuanti, graph = FALSE) 
## 
## 
## Eigenvalues
##                        Dim.1   Dim.2   Dim.3   Dim.4   Dim.5   Dim.6
## Variance               1.414   1.285   0.993   0.886   0.728   0.695
## % of var.             23.567  21.423  16.543  14.762  12.129  11.575
## Cumulative % of var.  23.567  44.991  61.533  76.296  88.425 100.000
## 
## Individuals (the 10 first)
##                           Dist    Dim.1    ctr   cos2    Dim.2    ctr   cos2  
## 1                     |  3.374 |  2.585  0.472  0.587 | -1.468  0.168  0.189 |
## 2                     |  2.085 | -1.587  0.178  0.579 |  1.300  0.132  0.389 |
## 3                     |  2.881 |  1.211  0.104  0.177 |  0.682  0.036  0.056 |
## 4                     |  3.341 |  1.654  0.194  0.245 |  2.010  0.314  0.362 |
## 5                     |  3.206 |  2.819  0.562  0.773 |  0.634  0.031  0.039 |
## 6                     |  3.465 |  1.143  0.092  0.109 |  2.341  0.426  0.457 |
## 7                     |  2.039 |  1.053  0.078  0.267 | -0.381  0.011  0.035 |
## 8                     |  1.930 | -0.848  0.051  0.193 |  1.470  0.168  0.580 |
## 9                     |  2.748 |  1.441  0.147  0.275 |  0.265  0.005  0.009 |
## 10                    |  1.896 | -0.409  0.012  0.046 | -0.153  0.002  0.007 |
##                        Dim.3    ctr   cos2  
## 1                     -0.751  0.057  0.050 |
## 2                     -0.227  0.005  0.012 |
## 3                      1.174  0.139  0.166 |
## 4                      0.220  0.005  0.004 |
## 5                      1.058  0.113  0.109 |
## 6                      0.277  0.008  0.006 |
## 7                     -1.349  0.183  0.437 |
## 8                     -0.554  0.031  0.082 |
## 9                     -1.502  0.227  0.299 |
## 10                     0.406  0.017  0.046 |
## 
## Variables
##                          Dim.1    ctr   cos2    Dim.2    ctr   cos2    Dim.3
## monto.credito         |  0.098  0.681  0.010 |  0.762 45.171  0.581 | -0.282
## porcentaje.disponible |  0.074  0.384  0.005 | -0.805 50.414  0.648 | -0.009
## residente             |  0.645 29.451  0.416 | -0.089  0.621  0.008 | -0.486
## edad                  |  0.738 38.494  0.544 | -0.067  0.350  0.005 | -0.198
## numero.creditos       |  0.522 19.285  0.273 |  0.012  0.011  0.000 |  0.393
## dependientes          |  0.407 11.703  0.165 |  0.210  3.433  0.044 |  0.695
##                          ctr   cos2  
## monto.credito          8.015  0.080 |
## porcentaje.disponible  0.009  0.000 |
## residente             23.826  0.236 |
## edad                   3.931  0.039 |
## numero.creditos       15.557  0.154 |
## dependientes          48.662  0.483 |

En el compartimiento $eig podemos ver los valores propios (eigenvalue) que están organizados de mayor a menor, el porcentaje de varianza explicado por cada componente (percentage of variance) y el porcentaje acumulado de varianza (cumulative percentage of variance). Por ejemplo, el primer componente explica el 23.57% de la varianza y los primeros tres componentes explican el 61.53% de la varianza.

Ahora decidamos el número de componentes óptimo (\(p\)). El gráfico de codo o scree plot se puede construir fácilmente empleando la función fviz_screeplot() del paquete factoextra (Kassambara & Mundt, 2020). .

library(factoextra)
fviz_screeplot(pca_inicial) + 
       labs(title="",
        x ="p (número de componentes principales)", 
        y = "% de varianza explicada") +
  theme_minimal()


Figura 5.3: Gráfico de codo

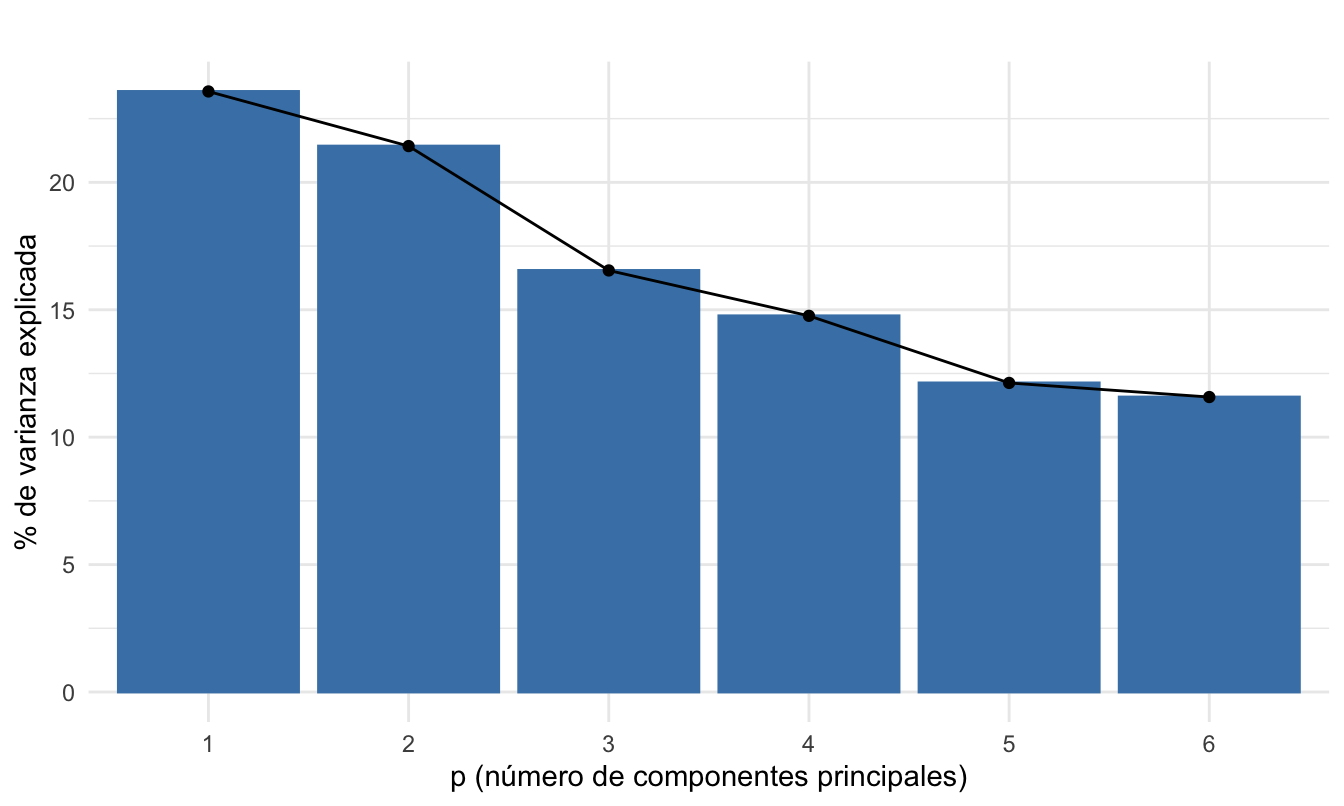
Gráfico de codo
Fuente: elaboración propia.



Recuerda que nuestro objetivo es encontrar los componentes que explican la mayor varianza. Pues, queremos conservar tanta información como sea posible utilizando el menor número de componentes. Entonces, cuanto mayor sea la varianza explicada, mayor será la información contenida en esos componentes.

De la Figura 5.3 podemos ver que el primer componente principal explica el 23.57% de la varianza. El segundo componente explica el 21.42%. Y así sucesivamente. En la Figura 5.3 debemos buscar el codo (elbow): el punto donde la curva se aplana. Es decir, donde no se empieza a agregar mucho a la varianza. En este caso, el codo aparece en el quinto componente y, por tanto, esto implicaría usar solo los componentes a la izquierda; es decir, 4 componentes. Con esos cuatro componentes podemos explicar el 76.3% de la varianza. Pero esto significaría una reducción muy baja de la dimensionalidad; de 6 a 4 variables.

Por otro lado, la regla de Keisser-Guttman implica mantener aquellos mayores a uno. Recordemos que los valores propios los podemos ver de manera muy sencilla con el siguiente código:

pca_inicial$eig
##        eigenvalue percentage of variance cumulative percentage of variance
## comp 1  1.4140252               23.56709                          23.56709
## comp 2  1.2854088               21.42348                          44.99057
## comp 3  0.9925758               16.54293                          61.53350
## comp 4  0.8857343               14.76224                          76.29573
## comp 5  0.7277376               12.12896                          88.42469
## comp 6  0.6945183               11.57531                         100.00000

Esta regla implicaría emplear 2 componentes. Ahora sí, sería una reducción sustancial de la nacionalidad.

Por otro lado, el análisis paralelo o análisis paralelo de Horn se puede implementar en R por medio de la función paran() del paquete paran (Dinno, 2018). Esta función necesita como argumentos los datos originales (la estandarización se hace de manera automática), si se desea una semilla para los cálculos aleatorios se puede fijar con el argumento seed y un argumento lógico para mostrar el gráfico (graph).

En este caso, el código con el que guardamos los resultados del análisis paralelo en el objeto pca_paralelo y creamos la Figura 5.4 es el siguiente:

library(paran)
pca_paralelo <- paran(german_cuanti, graph = TRUE, seed=0)



## 
## Using eigendecomposition of correlation matrix.
## Computing: 10%  20%  30%  40%  50%  60%  70%  80%  90%  100%
## 
## 
## Results of Horn's Parallel Analysis for component retention
## 180 iterations, using the mean estimate
## 
## -------------------------------------------------- 
## Component   Adjusted    Unadjusted    Estimated 
##             Eigenvalue  Eigenvalue    Bias 
## -------------------------------------------------- 
## 1           1.308144    1.414025      0.105880
## 2           1.231785    1.285408      0.053623
## -------------------------------------------------- 
## 
## Adjusted eigenvalues > 1 indicate dimensions to retain.
## (2 components retained)

Figura 5.4: Análisis paralelo de Horn para encontrar el número óptimo de componentes principales

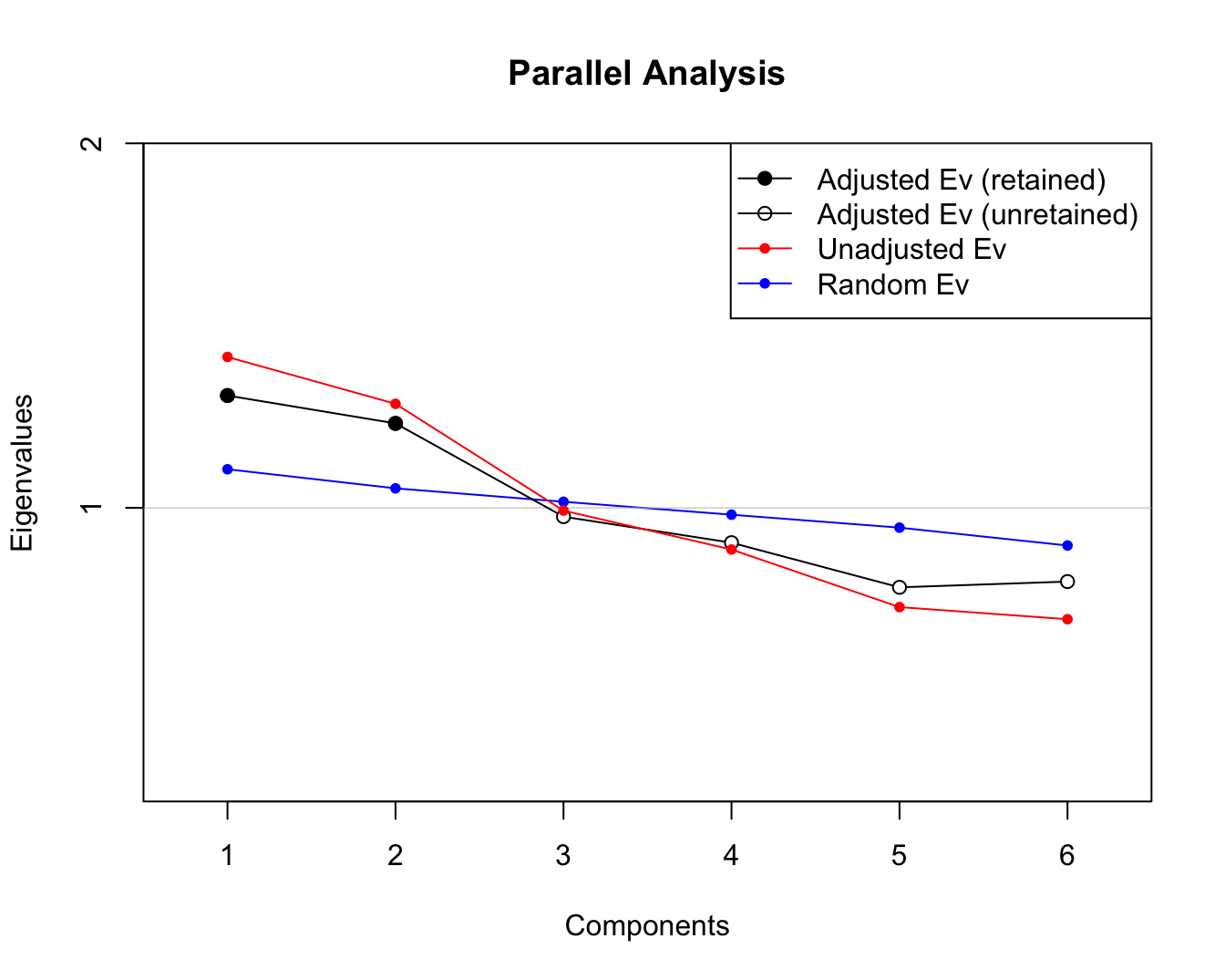
Análisis paralelo de Horn para encontrar el número óptimo de componentes principales
Fuente: elaboración propia.



En la Figura 5.4, los componentes principales “retenidos” (óptimos) se indican con marcadores circulares sólidos en la línea de color negro que corresponde al valor propio ajustado (Adjusted Ev) y los componentes principales no “retenidos” se indican con marcadores circulares sin relleno.

El número óptimo de componentes principales lo podemos encontrar en el compartimiento $Retained del objeto creado. Es decir,

pca_paralelo$Retained
## [1] 2

Este criterio sugiere mantener los 2 primeros componentes. De esta manera, tenemos que el criterio del codo sugiere 4 componentes, mientras que la regla de Keisser-Guttman y el análisis paralelo sugieren 2 componentes. Trabajaremos con 2 componentes que corresponden a una reducción sustancial de la dimensionalidad. Es importante mencionar que el análisis paralelo es considerado como una aproximación más sofisticada que las otras dos.

Ya hemos determinado que \(p=2\). Calculemos el PCA para dos componentes.

pca_final <- PCA(german_cuanti, graph = FALSE, ncp = 2)

Finalmente, el valor de los componentes principales lo podemos encontrar en el compartimiento $ind[1] del objeto creado.

5.5.2 Detencción de anomalías con el PCA en R

Ya hemos encontrado los componentes principales; es decir, hemos podido expresar las observaciones que tenemos para los mil individuos de las seis variables cuantitativas en dos componentes principales para cada uno de los individuos. Ahora la tarea es emplear esos componentes principales para detectar las observaciones anormales.

Típicamente, el primer paso es visualizar en un diagrama de dispersión los componentes principales encontrados para cada observación. Esto lo podemos hacer de muchas maneras. Una forma muy fácil es emplear la función fviz_pca_ind() del paquete factoextra (Kassambara & Mundt, 2020). Esta función solo necesita como argumentos un objeto de clase PCA (objeto donde guardamos los resultados del PCA) y determinar cuáles componentes principales se desean graficar. En nuestro caso solo encontramos dos componentes principales, pero en otras ocasiones podremos tener más y será interesante no solo graficar los primeros dos componentes principales sino por ejemplo el primero y el segundo. En nuestro caso, que solo queremos ver los dos primeros componentes principales, emplearemos axes = c(1, 2). El código sería el siguiente (intencionalmente no se muestra el gráfico resultante):

 fviz_pca_ind(pca_final, axes = c(1, 2))

Es también común incluir en esta visualización una elipse llamada elipse de confianza o elipse de dispersión. La elipse generalmente representa un intervalo de confianza alrededor de los datos (comúnmente del 97,5%) teniendo en cuenta la distancia de Mahalanobis (Para una discusión sobre este tema, ver la Sección 4.4). Los puntos que caen fuera de la elipse pueden considerarse outliers en el espacio de las componentes principales.

La elipse de dispersión la podemos construir con el argumento addEllipses = TRUE. El código para generar la Figura 5.4 es el siguiente:

 fviz_pca_ind(pca_final, axes = c(1, 2), addEllipses = TRUE)


Figura 5.5: Diagrama de dispersión para los dos componentes principales y su respectiva elipse de dispersión

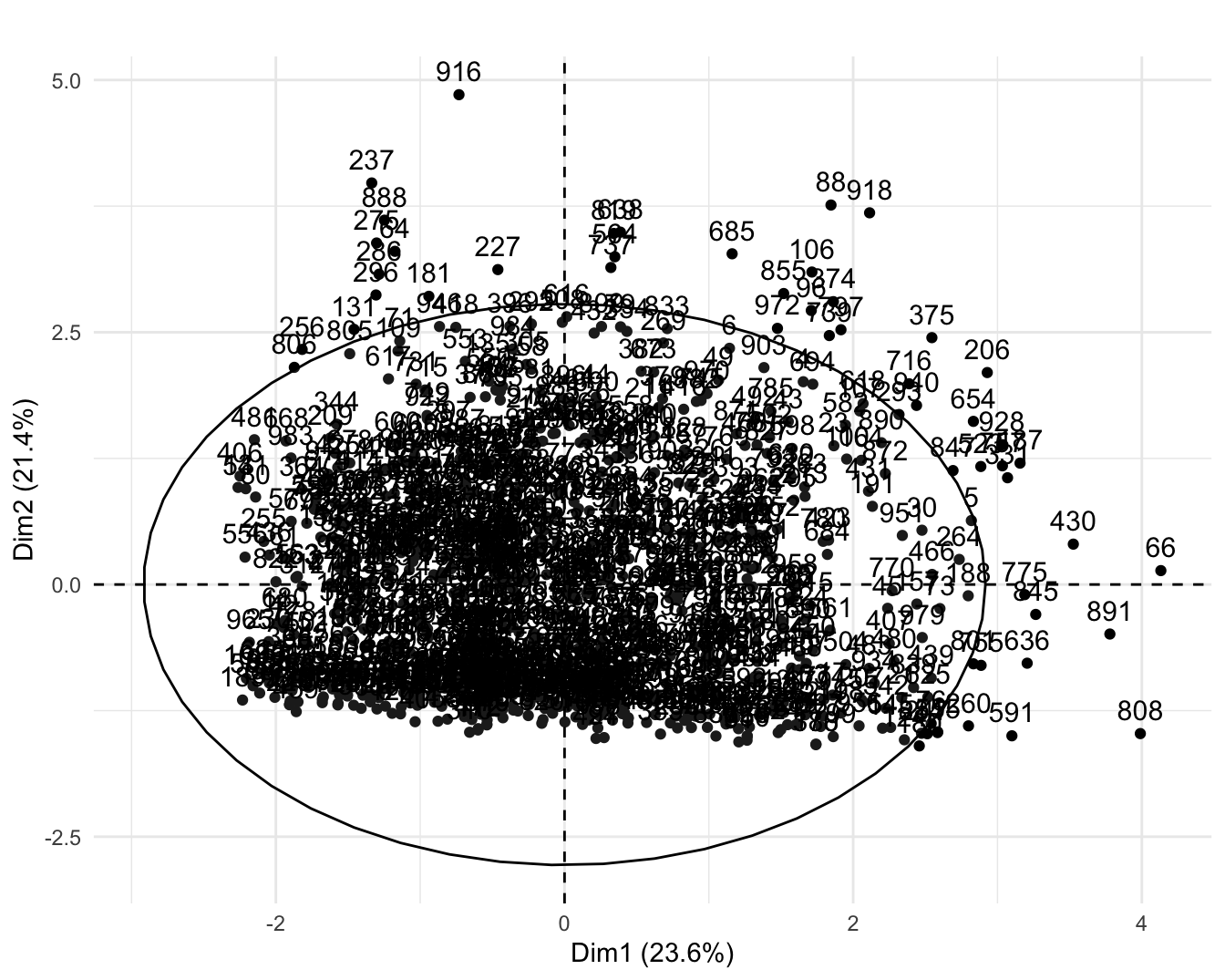
Diagrama de dispersión para los dos componentes principales y su respectiva elipse de dispersión
Fuente: elaboración propia.



En la Figura 5.4 cada punto representa una observación (\(i\)) y el número corresponde al número de la observación. Se puede observar que el individuo 916 tiene un valor anormalmente grande de la dimensión 2 (segundo componente principal) y el 66 en la dimensión 1.

Por otro lado, si queremos emplear la distancia de Mahalanobis, como se discutió en la Sección 5.4, existe la función pca.outlier() del paquete mt (Lin, 2024). Esta función detecta automáticamente los valores atípicos empleando las distancias de Mahalanobis de los primeros dos componentes principales. Adicionalmente, permite visualizar los componentes principales 1 y 2 en un gráfico de dispersión con su elipse de confianza, empleando la distancia de Mahalanobis.

La función típicamente incluye los siguientes argumentos:

pca.outlier(x, center, scale, conf.level)

donde:

  • x: Es un objeto de clase matrix o data.frame que contiene los datos originales \(\textbf{X}_{n \times d}\) (sin estandarizarse).
  • center: Si center = TRUE (valor por defecto) se le resta a los datos la media (se centran) para que tengan una media cero antes del PCA.
  • scale: Si scale = TRUE (valor por defecto) se escalan los datos para que cada variable tenga varianza 1 antes del PCA.
  • conf.level: El nivel de confianza para controlar el corte de las distancias de Mahalanobis. Es decir, para la construcción de las elípses.
# Cargar paquete
library(mt)

outlier_mahala <- pca.outlier(german_cuanti, 
                              center = TRUE, scale=TRUE, 
                              conf.level = 0.975)

En el objeto outlier_mahala podemos encontrar en el compartimiento $outlier los puntos que quedan por fuera de la elipse de dispersión; es decir, los outliers. Y si invocas el objeto outlier_mahala podrás ver la visualización de los componentes principales 1 y 2 en un gráfico de dispersión con su elipse de confianza, empleando la distancia de Mahalanobis, tal como se presenta en la Figura 5.6.



Figura 5.6: Diagrama de dispersión para los dos componentes principales y su respectiva elipse de dispersión empleando la distancia de Mahalanobis

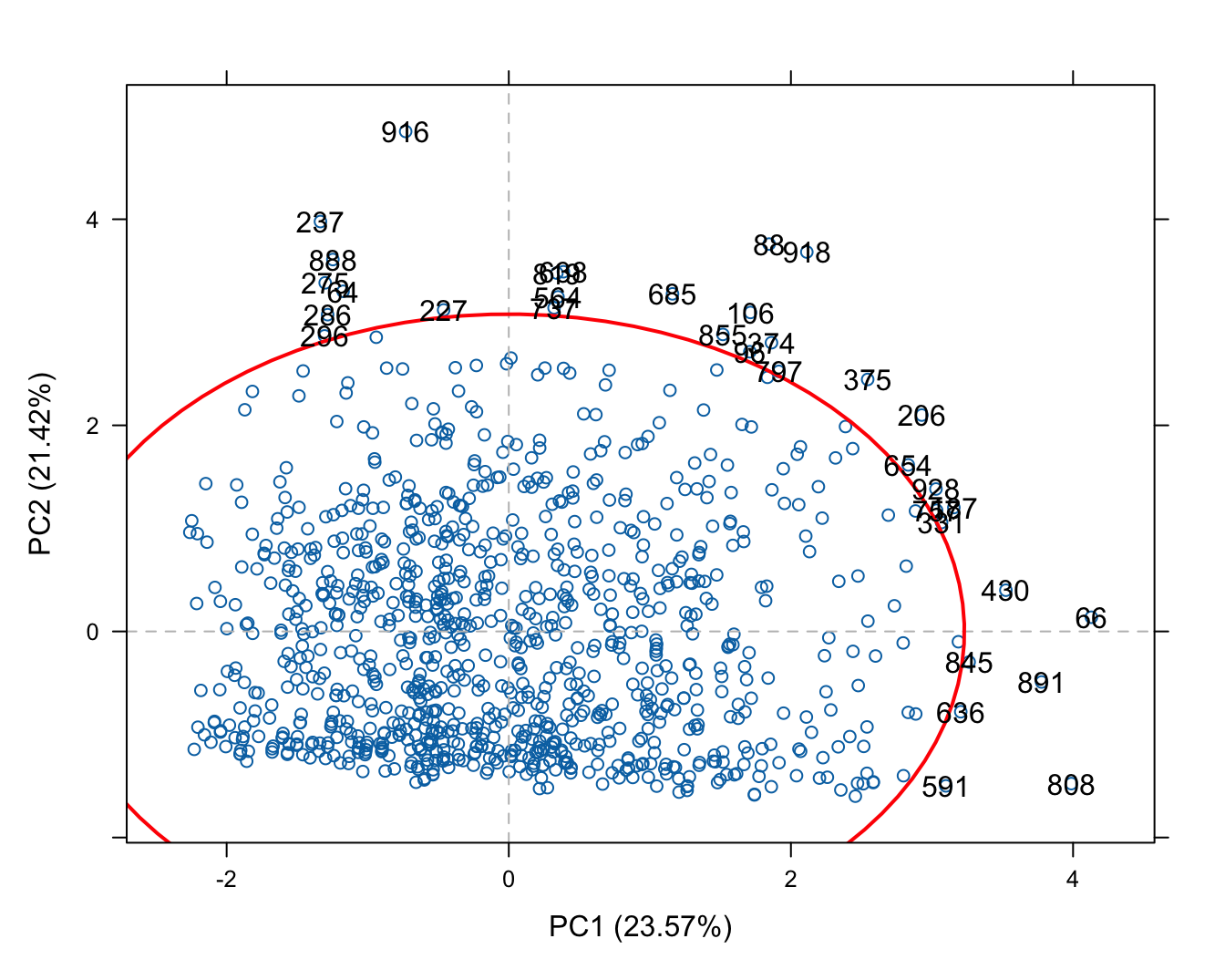
Diagrama de dispersión para los dos componentes principales y su respectiva elipse de dispersión empleando la distancia de Mahalanobis
Fuente: elaboración propia.



De acuerdo con esta aproximación, tenemos 34 outliers.

Finalmente, para calcular el score de anomalías, según la expresión (5.9), hemos construido la siguiente función:

score.anomal.PCA <- function(X, p ){
  # X = objeto de clase PCA con el análisis de PCA
  # p = número de Componentes principales
  
  eig <- t(as.matrix(X$eig[1:p,1])) # Extraer los valores propios
  CP <-  X$ind[1] # Extraer los componentes principales
  CP <-  as.matrix(CP$coord)  
  temp<- CP^2 / matrix( data = rep(eig, dim(CP)[1]), ncol = p)
  scores <-  apply(CP^2 / matrix( data = rep(eig, dim(CP)[1]), ncol = p), 1, sum )
  scores <- as.data.frame(scores)
  
  scores <- cbind(rownames(scores), scores)
  names(scores) <- c("Id de la observación", "Score de anomalía")

  scores <- scores[order(scores$`Score de anomalía`, decreasing = TRUE),]
  return(scores)
}

Para nuestro caso, podemos calcular el score de anomalía para todas las observaciones empleando el siguiente código:

score_PCA <- score.anomal.PCA(X= pca_final, p=2)
# mirar las 5 observaciones con mayor score de anomalía
head(score_PCA, 5)
##     Id de la observación Score de anomalía
## 916                  916          18.74997
## 808                  808          14.08165
## 918                  918          14.03348
## 88                    88          13.65659
## 66                    66          13.29652

Nota que la observación con el score de anomalía más grande es la 916. También podemos visualizar todos los scores con un boxplot (ajustado según Hubert y Vandervieren (2008)) como el que se presenta en la Figura 5.749.



Figura 5.7: Boxplot ajustado según Hubert y Vandervieren (2008) para los scores de anomalía

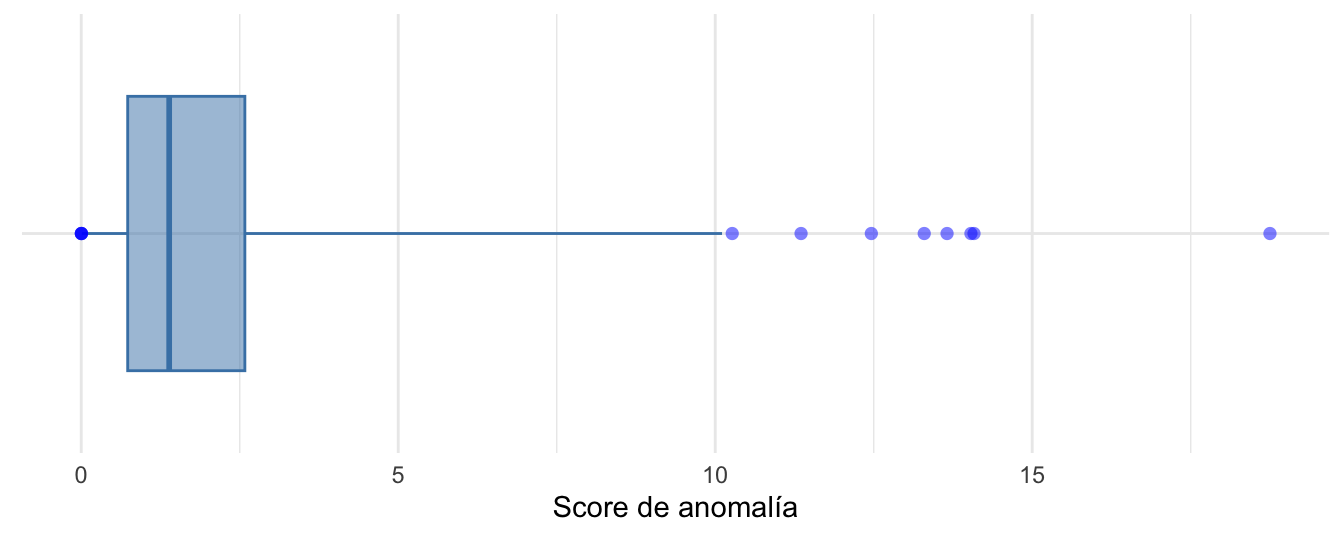
Boxplot ajustado según Hubert y Vandervieren (2008) para los scores de anomalía
Fuente: elaboración propia.

En la Figura 5.7 podemos ver que existen 12 valores atípicos. Es decir, observaciones con scores de anomalía relativamente grande.

5.6 Comentarios finales

En este capítulo estudiamos cómo emplear la técnica del PCA para detectar outliers multivariados. Esta técnica, al igual que las estudiadas en los Capítulos 2, 3 y 4 permite encontrar anomalías que se pueden caracterizar como anomalías globales.Global}

Recordemos que las anomalías globales son observaciones que son atípicas en relación con todo el conjunto de datos. Estas observaciones son inusuales no solo en su entorno inmediato, sino también en comparación con todas las demás observaciones, ya sea que estemos estudiando datos univariados o multivariados. Las anomalías globales suelen ser puntos extremadamente raros o inesperados en el contexto del conjunto de observaciones en su totalidad.

Por otro lado, las anomalías locales son observaciones que son atípicas en relación con su entorno inmediato. Esto significa que, aunque una observación pueda ser considerada normal en el contexto global de todas las observaciones, puede ser considerada una anomalía si se compara con sus vecinos más cercanos. En el Capítulo 8 empezaremos el estudio de herramientas para detectar este tipo de anomalías. Pero antes de pasar a estudiar esas herramientas, tomaremos un desvío en nuestro camino para discutir en el Capítulo 6 que es un fraude y cómo este concepto está relacionado con las anomalías. Así mismo, discutiremos una técnica estadística para detectar fraudes que se conoce como la Ley de Benford.



Referencias

Alonso, J. C. (2020). Herramientas del Business Analitycs en R: Análisis de Componentes Principales para resumir variables (Icesi Economics Lecture Notes No. 18188). Universidad Icesi. https://ideas.repec.org/p/col/000559/018188.html
Alonso, J. C. (2024). Introducción al modelo clásico de regresión para científico de datos en r. Universidad Icesi. https://doi.org/https://doi.org/10.18046/EUI/bda.h.4
Bougeard, S., & Dray, S. (2018). Supervised multiblock analysis in R with the ade4 package. Journal of Statistical Software, 86(1), 1–17. https://doi.org/10.18637/jss.v086.i01
Dinno, A. (2018). Paran: Horn’s test of principal components/factors. https://CRAN.R-project.org/package=paran
Hofmann, H. (1994). Statlog (German Credit Data). UCI Machine Learning Repository.
Horn, J. L. (1965). A rationale and test for the number of factors in factor analysis. Psychometrika, 30(2), 179–185. https://doi.org/10.1007/BF02289447
Kassambara, A., & Mundt, F. (2020). Factoextra: Extract and visualize the results of multivariate data analyses. https://CRAN.R-project.org/package=factoextra
Lê, S., Josse, J., & Husson, F. (2008). FactoMineR: A package for multivariate analysis. Journal of Statistical Software, 25(1), 1–18. https://doi.org/10.18637/jss.v025.i01
Lin, W. (2024). Mt: Metabolomics data analysis toolbox. https://CRAN.R-project.org/package=mt
Lucas, A. (2022). Amap: Another multidimensional analysis package. https://CRAN.R-project.org/package=amap
Nenadic, O., & Greenacre, M. (2007). Correspondence analysis in r, with two- and three-dimensional graphics: The ca package. Journal of Statistical Software, 20(3), 1–13. http://www.jstatsoft.org
Venables, W. N., & Ripley, B. D. (2002). Modern applied statistics with s (Fourth). Springer. https://www.stats.ox.ac.uk/pub/MASS4/
Wickham, H., François, R., Henry, L., & Müller, K. (2021). Dplyr: A grammar of data manipulation. https://CRAN.R-project.org/package=dplyr
William Revelle. (2023). Psych: Procedures for psychological, psychometric, and personality research. Northwestern University. https://CRAN.R-project.org/package=psych

  1. Partes de este documento provienen de unas notas de clase que se publicaron en Alonso (2020). En dicho documento se presenta con mayor detalle cómo funciona la técnica del PCA.↩︎

  2. Por ejemplo, la media de la variable \(j\) sería \(\bar{x_j}=\frac{\sum_{i=1}^{n}x_{j,i}}{n}\).↩︎

  3. Intencionalmente se omite el código que genera la Figura 5.7. ¡Intenta reproducir esta visualización!↩︎